
3.2. Синхронизация автогенератора с несогласованной линией задержки
Используем полученные выше результаты для автогенератора с несогласованной линией задержки ПАВ. Это интересно с той точки зрения, что в схеме отсутствуют индуктивные элементы, наиболее трудоемкие при пленочной реализации автогенератора.
Как было показано выше, неизохронные свойства автогенератора с ЛЗ ПАВ определяются как нелинейными инерционными свойствами АЭ, т. е. зависимостью фазы крутизны выходного тока АЭ от амплитуды входного напряжения, так и частотными свойствами его линейной резонансной системы. Проявление нелинейных инерционных свойств АЭ в общих чертах аналогично их проявлению в неизохронных LC-генераторах, которые достаточно хорошо изучены. Поэтому далее будем считать, что фаза крутизны выходного тока АЭ не зависит от амплитуды колебаний, т. е. S⊥ = 0. В этом случае неизохронность рассматриваемого автогенератора будет определяться лишь частотными свойствами линейной резонансной системы автогенератора.
Для простоты рассмотрим симметричную схему автогенератора. Поскольку рассматривается автогенератор с несогласованной ЛЗ ПАВ, то выполняется условие слабого (прохождения ПАВ через ЛЗ ЛАВ (см. § 2.2, 2.4). Коэффициенты укороченных уравнений синхронизированного автогенератора (3.1) в предположении, что
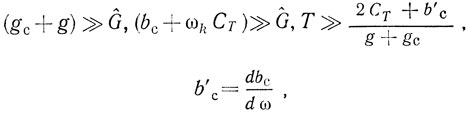
имеют вид
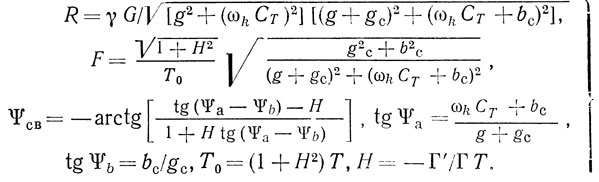
При условии слабого влияния проводимости связи Yc на линейную резонансную систему автогенератора собственные частоты и управляющее сопротивление равны
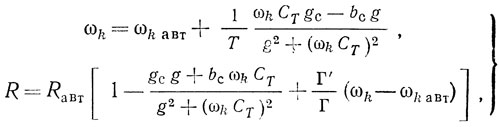
где ωk авт, Rавт - собственная частота линейной резонансной системы и управляющее сопротивление автономного автогенератора (под автономным автогенератором в данном случае подразумевается автогенератор без синхронизирующего источника и Yс = 0).
Из (3.6) и (3.7) следует, что при gcωkCT = gbc собственная частота резонансной системы синхронизированного генератора равна собственной частоте резонансной системы автономного генератора, а фаза Ψсв определяется лишь значением параметра неизохронности Н:
Yсв = arctg H.
Полоса слабой внешней синхронизации рассматриваемого автогенератора
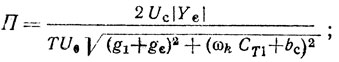
она пропорциональна величине 2Uc/TU0.
При gc << g1 и bс << ωkСТ1, т. е. при условии, что проводимость Yс существенно меньше проводимости резонансной системы Y автономного генератора, из (3.8) получим
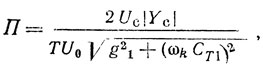
Разность фаз Δ в зависимости от величины расстройки в пределах полосы синхронизации П изменяется в соответствии с формулой
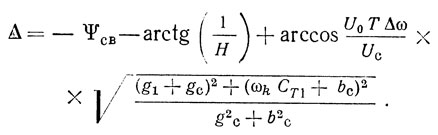

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
