§ 6. Энергетические показатели УРУ с однородной анодной линией

Рассмотрим теперь энергетические показатели лампового усилителя в режиме колебаний первого рода, пренебрегая частотной зависимостью выходного напряжения, которую можно сделать весьма малой при использовании фильтров типа m.

Выходная мощность УРУ

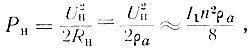
где I₁ = SU_вх - амплитуда первой гармоники анодного тока ламп УРУ.

Из полученного выражения видно, что выходная мощность УРУ с увеличением числа ламп возрастает пропорционально их квадрату. Этот интересный факт существенно отличает УРУ от других усилительных схем, построенных на принципе сложения мощностей.

Нетрудно найти коэффициент усиления мощности для УРУ, используя выражение (16):

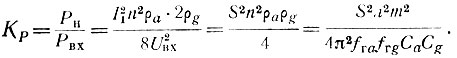
При определении к. п. д. воспользуемся кусочно-линейной аппроксимацией анодных характеристик лампы, предполагая, что в области недонапряженного режима анодный ток не зависит от анодного напряжения (рис. 13, а).

Введем здесь новые определения. Будем называть критическим режимом УРУ такой режим его работы, когда одна из ламп усилителя работает в критическом режиме хотя бы на одной частоте, но ни одна из ламп не работает в перенапряженном режиме. Будем называть недонапряженным режимом такой режим УРУ, когда все лампы в диапазоне частот работают в недонапряженном режиме. И наконец, режим УРУ, когда хотя бы одна его лампа работает в перенапряженном режиме, назовем перенапряженным.

Будем предполагать, что аноды всех ламп УРУ питаются от одного источника анодного питания с напряжением Е_а. Как будет показано в следующем параграфе, переменное напряжение на анодах ламп УРУ меньше или равно выходному напряжению УРУ. Поэтому для обеспечения критического режима усилителя постоянное анодное напряжение выбирается равным:

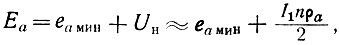
где е_амин - минимальное мгновенное значение напряжения на аноде лампы в критическом режиме (рис. 13, а).

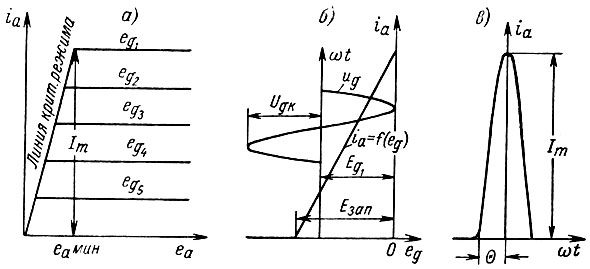
Рис. 13. Аппроксимированные анодные характеристики ламп (а), анодно-сеточная характеристика лампы (б) и форма импульса анодного тока лампы (в)

К. п. д. усилителя в критическом режиме определится следующим образом:

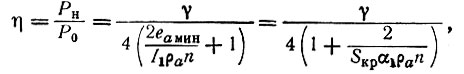
где Р₀ = nЕ_аI₀ - мощность, подводимая к УРУ от источника анодного питания; I₀ - постоянная составляющая анодного тока ламп; γ = I₁/I₀ - коэффициент формы анодного тока ламп, I_m - максимальное мгновенное значение анодного тока ламп в критическом режиме (рис. 13, a); S_кр = I_m/е_амин - для пентодов это отношение представляет собой крутизну линии критического режима (рис. 13, а); α₁ = I₁/I_m - коэффициент первой гармоники анодного тока ламп.

В предельном режиме класса А(α₁ = 0,5; γ = 1) выражение для к. п. д. принимает вид:

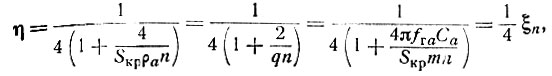
где ξ_n = U_н/E_a - коэффициент использования анодного напряжения для n-й лампы; q = 0,5 S_крρ_a.

Из последней формулы видно, что максимально достижимое значение к. п. д. усилителя с распределенным усилением составляет 0,25, в то время как для обычных усилительных устройств при тех же условиях предельное значение к. п. д. в классе А равно 0,5 [3,4].

На первый взгляд может показаться, что причиной низкого предельного значения к. п. д. УРУ являются потери мощности в балластном сопротивлении. Рассмотрим этот вопрос более детально.

Найдем напряжение на балластном сопротивлении для случая характеристического согласования линий УРУ. Для этого просуммируем напряжения, создаваемые на балластном сопротивлении каждой лампой (рис. 7, в):

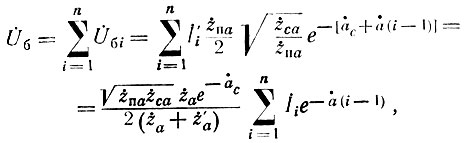
где İ_i = SU̇_gi.

Подставляя в последнее выражение формулу (5), получим при а̇ = ġ и I_i = const = I₁

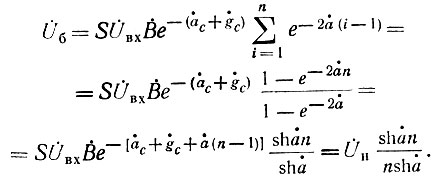
Мощность потерь в балластном сопротивлении в полосе прозрачности звеньев анодной линии

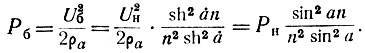
Как видно из рис. 14, на концах диапазона частот (х → 0, х → 1) мощность потерь в балластной нагрузке равна мощности в полезной нагрузке УРУ, вследствие чего к. п. д. уменьшается в два раза по сравнению с к. п. д. обычных усилителей. Однако в средней части диапазона, ширина которой при большом п может быть значительной, Р_б << P_н. Следовательно, на этих частотах потери в балластном сопротивлении не являются причиной низкого к. п. д. и для выяснения этой причины необходимо рассмотреть режимы и энергетические показатели каждой отдельной лампы, которые определяют результирующие энергетические показатели УРУ.

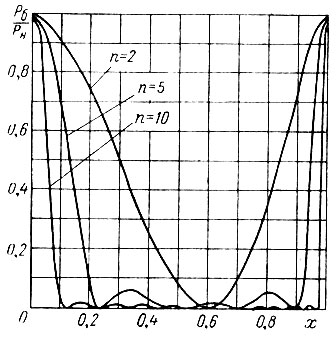
Рис. 14. Зависимость нормированной мощности потерь в балластном сопротивлении от относительной частоты для различных n