8.3. Кодирование с предсказанием

В ряде важных случаев, например при передаче речи, телевизионных изображений, данных телеметрии, между отсчетами передаваемых сообщений имеются статистические, в частности корреляционные, связи. Наличие таких взаимосвязей позволяет повысить эффективность систем передачи информации^*. Рассмотрим один из распространенных способов передачи - способ передачи с предсказанием (рис. 8.5). Последовательность коррелированных отсчетов b(kΔt)=b(k) исходного сигнала подают на один из входов вычитающего устройства, а на его другой вход поступает сигнал предсказания b(k), сформированный из предыдущих отсчетов. Полученный таким образом сигнал ошибки предсказания s(k) поступает в тракт передачи. Поскольку в сигнале ошибки как раз и содержатся новые сведения, представляющие разность между истинным и предсказанным значениями, то такой способ передачи называется передачей с предсказанием. Для упрощения считаем, что помехи в канале ошибок не создают. На приемном конце имеется такой же предсказатель, как и на передающем. Поскольку он оперирует с теми же предыдущими отсчетами, предсказанное им значение нового отсчета b̂̃(k) будет таким же, как и на передатчике. Добавив к нему принятое значение ошибки предсказания ε̂(k), можно восстановить истинный отсчет:

b(k) = b̃̂(k) + ε̂(k). (8.16)

^* (Как было показано в § 2.2, формула (2.48), значения отсчетов, взятых через интервал Котельникова, взаимно-некоррелированы, если спектр сообщения в занимаемой им полосе частот равномерен. Но на практике приходится часто передавать сообщения с неравномерным спектром (например, речь, телевидение), да к тому же частоту отсчетов по ряду соображений выбирают несколько выше, чем по Котельникову. Поэтому корреляция между отсчетами обычно не равна нулю.)

Рис. 8.5. Структурная схема системы связи с предсказанием

Очевидно, что чем сильнее корреляционные связи, тем точнее можно сформировать сигнал предсказания и, следовательно, тем меньшая энергия потребуется для передачи сигнала ошибки по сравнению с исходным сигналом. При сильных корреляционных связях, а также при марковских сообщениях, значение b̃(k) может быть предсказано по одному предыдущему отсчету:

Обычно можно получить достаточно малую ошибку предсказания, положив

откуда

Действительно, для средней энергии сигнала ошибки по ансамблю

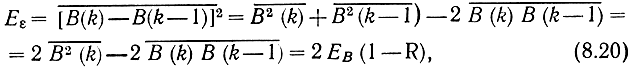
где

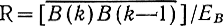
- коэффициент корреляции между отсчетами. Из (8.20) следует, что при R>0,5 энергия сигнала ошибки Ее меньше энергии исходного сигнала Е_в.

При цифровых системах передачи отсчеты сигнала ошибки подвергают обычным операциям квантования и кодирования. Результатом такого преобразования на передающей стороне является импульсно-кодовое представление сигнала ошибки, или сигнал дифференциальной импульсно-кодовой модуляции (ДИКМ). В настоящее время известно большое число вариантов технического осуществления кодирования с предсказанием. Основное их различие сводится к различию операций формирования сигнала ошибки: в одних системах сигнал ошибки формируется в аналоговой форме, а затем кодируется, в других - вначале кодируется исходный аналоговый сигнал, а затем формируется сигнал ошибки.

В системах с ДИКМ обычно применяют неравномерное квантование сигнала ошибки, так как наиболее вероятны малые ошибки. Поскольку мощность шума квантования составляет определенную долю мощности квантуемого процесса, а мощность ошибки предсказания, как правило, существенно меньше мощности сообщения, шум квантования при ДИКМ меньше, чем при обычной ИКМ при том же числе уровней.

Как показывает анализ, система ДИКМ обеспечивает одинаковое с ИКМ качество передачи при меньшем числе символов в кодовой комбинации (на один-два и более символов в зависимости от степени корреляции отсчетов и от алгоритма предсказания).

Шум ложных импульсов также имеет место при ДИКМ, причем он ухудшает верность приема в большей мере, чем при обычной ИКМ. Дело в том, что ошибочный прием кодовой комбинации ведет к ошибочному приему не только одного отсчета сообщения, но и ряда последующих отсчетов, поскольку предсказанные значения на приемной стороне будут отличаться от предсказанных на передатчике. Поэтому допустимая вероятность ошибок при ДИКМ меньше, чем при ИКМ, и, следовательно, пороговая мощность сигнала выше. Существуют различные способы уменьшения влияния "размножения" ошибок.

Корреляция между отсчетами возрастает по мере сокращения интервала между ними. Поэтому при большой частоте дискретизации число уровней квантования сигнала ошибки можно уменьшить до двух и перейти к одноразрядным системам. Такой способ кодирования называют дельта-модуляцией.

Квантованный сигнал ошибки имеет вид

где

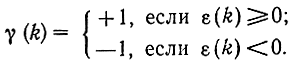
По существу, сигнал на выходе дельта-модулятора содержит лишь сведения о полярности (знаке) сигнала ошибки. На приемной стороне интегратор прибавляет или вычитает Δb, обеспечивая, таким образом, уменьшение погрешности между исходными значениями отсчетов и восстановленными значениями. Принцип формирования сигнала дельта-модуляции показан на рис. 8.6. Отсчеты b(k) передаваемого сообщения сравниваются с квантованным отсчетом b̃_KB(k-1), полученным в результате суммирования всех предыдущих квантованных сигналов ошибки:

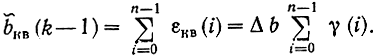
Если b (k)>b̃_KB(k-1), квантователь формирует значение γ(k) = 1, в противном случае γ(k) = - 1. Полученные символы у передаются по тракту связи (рис. 8.7,6). Одновременно импульсы Δbγ(i) поступают на сумматор (интегратор) для формирования квантованного отсчета b_KB(i), который, как указывалось выше, сравнивается с очередным отсчетом сообщения. На выходе сумматора квантованный сигнал b̃_KB(t) имеет вид ступенчатой функции (рис. 8.7,а). Каждый импульс +1 увеличивает, а каждый импульс -1 уменьшает ступенчатую функцию на один шаг квантования (рис. 8.7,а), т. е. при ДМ соседние значения ступенчатой функции различаются обязательно на один шаг квантования.

Рис. 8.6. Структурная схема системы с дельта-модуляцией

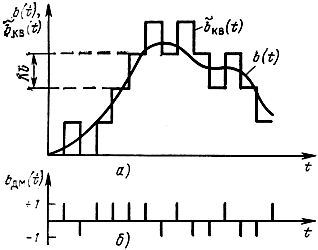
Рис. 8.7. Графики, поясняющие принцип формирования сигналов дельта-модуляции

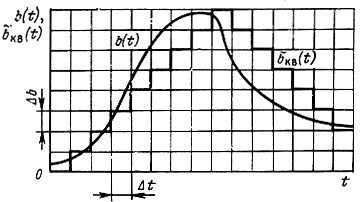
Рис. 8.8. График, поясняющий возникновение искажений из-за перегрузки по наклону при дельта-модуляции

Операцию декодирования сигнала ДМ на приемной стороне выполняет сумматор (интегратор), такой же, как и на передающей стороне, на выходе которого (при отсутствии ложных импульсов) получается ступенчатое напряжение b̂_КВ (t). После его сглаживания с помощью фильтра получим функцию b(t), достаточно близкую к b(t). Разность b̂(t)-b(t) представляет шум квантования. Его значение тем меньше, чем выше частота дискретизации и чем меньше шаг Δb. Однако шаг квантования Δb нельзя выбирать слишком малым. В противном случае возникают дополнительные искажения, называемые "перегрузкой по наклону", вызванные тем, что ступенчатая функция не успевает следить за быстрыми изменениями сообщения b(t) (рис. 8.8). Если принять, что максимальное значение крутизны изменения сообщения составляет |b'(t) |_max, то для неискаженной передачи необходимо выполнить условие | b'(t) | _maxΔt≤Δb. Если практически максимальное значение сообщения по модулю не превышает | b(t)|_max, а число различных уровней квантования, определяющее шум квантования, равно L, то

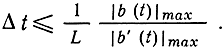(8.22)

По сравнению с ИКМ и ДИКМ сигналы ДМ имеют значительно более высокую частоту следования отсчетов. Однако на каждый отсчет при ДМ передается один импульс, а при ИКМ - несколько, в зависимости от числа уровней. Как показывает анализ, при одинаковой верности передачи частота следования импульсов при ИКМ и ДМ также примерно одинакова. Поэтому обе эти системы занимают приблизительно одинаковую полосу частот. Существенным преимуществом систем передачи с ДМ является сравнительная простота кодирующих и декодирующих устройств. Кроме

того, шум ложных импульсов при ДМ меньше, чем при ИКМ (при той же вероятности ошибки в канале), поскольку при ДМ каждая ошибка изменяет уровень сигнала только на ±2Δb. К недостаткам ДМ можно отнести явление размножения ошибок, создаваемых ложными импульсами (такое же, как и при ДИКМ), а также возможность перегрузки по наклону.

Отметим, что в последние годы успешно разрабатываются многочисленные разновидности ДИКМ и ДМ, в частности адаптивные системы, в которых для уменьшения шумов квантования используют переменный шаг квантования в зависимости от текущих статистических характеристик передаваемого сообщения.

В качестве примера на рис. 8.9,а приведена структурная схема кодера адаптивной ДМ. Характерной особенностью является наличие в цепи обратной связи решающего устройства, управляющего величиной шага квантования Δb. Если знак приращений γ(k) остается неизменным в течение трех-четырех интервалов дискретизации, то это означает наличие перегрузки (рис. 8.9,6). Решающее устройство удваивает амплитуду импульсов, поступающих на вход интегратора 1. Если и в этом случае знак приращения (сигнала ошибки) не изменится, то размер шага Δb снова удваивается и т. д. При изменении знака приращения размер шага квантования уменьшается. Нетрудно понять, что в состав устройства управления размером шага квантования должен входить анализатор плотности единиц и импульсный усилитель с управляемым коэффициентом усиления. На выходе интегратора 2 при изменении коэффициента усиления в зависимости от плотности единиц будет формироваться ступенчатое напряжение с адаптивно изменяющимся шагом квантования (рис. 8.9,6).

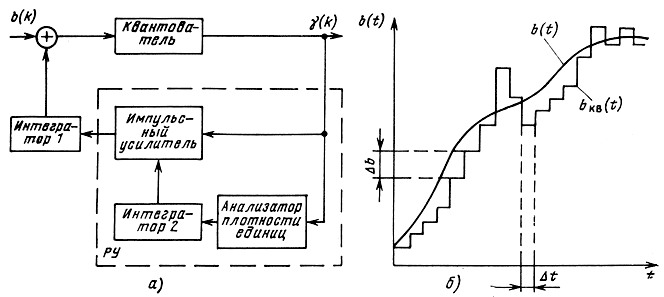
Рис. 8.9. Структурная схема кодера адаптивной ДМ (а): изменение шага квантования при адаптивной ДМ (б)

Вопросы к главе 8

1. В чем заключаются основные преимущества цифровых методов передачи непрерывных сообщений ?
2. Составьте структурную схему цифровой системы передачи. Поясните назначение отдельных узлов.
3. Поясните принцип действия АЦП и ЦАП, сформулируйте требования, предъявляемые к ним.
4. Сформулируйте сущность ИКМ. Поясните принципиальное различие между шумом квантования и помехами в канале передачи.
5. * Выведите формулу для отношения средних мощностей сообщения и шума квантования при условии, что мгновенные значения сообщения имеют нормальное распределение. Поясните, какой ценой достигается улучшение отношения сигнал-шум при квантовании.
6. В чем заключаются преимущества цифровой передачи с компандированием?
7. Поясните принцип действия цифровых систем с предсказанием.
8. Поясните принцип действия, достоинства и недостатки систем передачи с дельта-модуляцией.
9. Поясните принцип действия и преимущества систем передачи с адаптивной дельта-модуляцией.
10. * Существует ли корреляция между сигналом и шумом квантования в системе ИКМ с равномерным (линейным) квантованием и в системе с неравномерным квантованием (мгновенным компандированием)?