9.3. Разделение сигналов по форме

Для разделения сигналов могут использоваться не только такие очевидные признаки, как частота, время и фаза. Наиболее общим признаком является форма сигналов. Различающиеся по форме сигналы могут передаваться одновременно и иметь перекрывающиеся частотные спектры, и тем не менее такие сигналы можно разделить, если выполняется условие их линейной независимости или условие ортогональности. Пусть в качестве переносчиков выбраны импульсы, последовательность которых образует, например, степенной ряд:

В предположении, что информация содержится в коэффициентах С₁, С₂ для группового сигнала запишем

Члены ряда (9.18) линейно-независимы, и, следовательно, ни один из канальных сигналов c_kt^k не может быть образован линейной суммой всех других сигналов. Это легко понять, обратив внимание на то, что многочлен от t вида (9.19) может быть тождественно равен нулю только в том случае, когда все его коэффициенты равны нулю.

Для разделения таких сигналов можно применить общий метод в соответствии с условием линейной независимости переносчиков (9.6). Так, при двухканальной передаче имеем для интервала 0≤t≤T

если далее весовые функции выбрать удовлетворяющими условиям разделения:

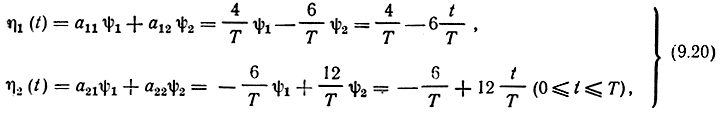
то в результате операций проектирования

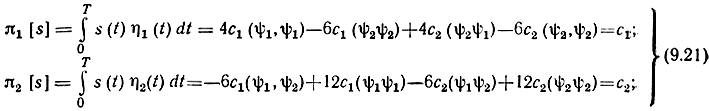
[здесь (ψ₁ψ₁) = 1, (ψ₂ψ₂) =1/3, (ψ₁ψ₂) = (ψ₂ψ₁) = 1/2].

Операции (9.21) выполняются разделяющим устройством, изображенным на рис. 9.8. В отличие от устройств разделения ортогональных сигналов здесь добавляется устройство формирования весовых функций (η₁ и η₂), которое из функций ψ₁ и ψ₂ образует линейные комбинации вида (9.20).

При выборе сигналов для систем многоканальной связи с разделением по форме часто используется ортогонализация сигналов - операция преобразования линейно-независимых сигналов в ортогональные.

В последние годы успешно развиваются цифровые методы разделения сигналов по их форме, в частности, в качестве переносчиков различных каналов используются дискретные ортогональные последовательности в виде функций Уолша, Радемахера и другие. Функции Радемахера образуются из синусоидальных функций с помощью соотношения: r_k(θ) = sign [sin (2^kπθ)], 0≤θ<1, где аргумент θ = t/T- безразмерное время; Т - период функции, а положительное целое число k = 0, 1, 2, ... - порядок функции; sign х- знак действительного числа х; sign x = + 1 при x>0 и sign x = -1 при х<0. Иначе говоря, функции Радемахера, принимающие значения ±1, можно трактовать как функции "прямоугольного синуса". На рис. 9.9 приведены в качестве примера графики первых четырех функций Радемахера r_k(θ) для k = 0, 1, 2, 3. Легко видеть, что функции r_k(θ) ортонормированы на интервале 0≤θ<1:

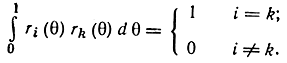
Дальнейшим развитием системы функций, имеющих форму "прямоугольной волны", является система функций Уолша {wal(m, θ)}. Она образуется следующим образом. По определению вводится функция wal(0, θ) = 1 при m = 0.

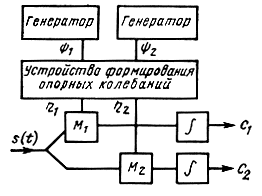
Рис. 9.8. Структурная схема разделения линейно-независимых сигналов

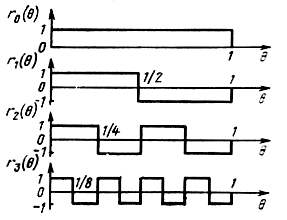
Рис. 9.9. Графики первых четырех функций Радемахера

Для получения функции wal(m, θ) при m≥1 достаточно записать число т в; двоичной системе счисления, т. е. представить суммой

где μ₁<μ₂<...<μ_p - положительные целые числа. При этом функция Уолша

Порядок k функции Уолша wal_k(θ) равен числу знакоперемен "на интервале (0, 1/2) и определяется как k = m/2 для четных m и k = (m+1)/2 для нечетных m. На рис. 9.10 приведены графики первых восьми функций Уолша wal(0, θ), wal(1, θ), ..., wal (7, θ), построенных по четырем функциям Радемахера.

Функции Уолша не только ортогональны, они обладают свойством мультипликативности. Это означает, что произведение любых двух функций Уолша также является функцией Уолша: wal(i, θ) wal(k, θ) = wal(p, θ), где р = i⊕k. В связи с возможностью применения к функциям Уолша логических операций, они являются весьма перспективными при разработке многоканальных цифровых систем передачи с разделением по форме, а также в аппаратуре формирования и преобразования сигналов на базе микропроцессорной техники.

Широкое развитие методов разделения по форме сигналов привело к созданию систем передачи с разделением "почти ортогональных" сигналов, представляющих собой псевдослучайные последовательности, корреляционные функции и энергетические спектры которых близки к аналогичным характеристикам "ограниченного" белого шума. Такие сигналы называют шумоподобными.

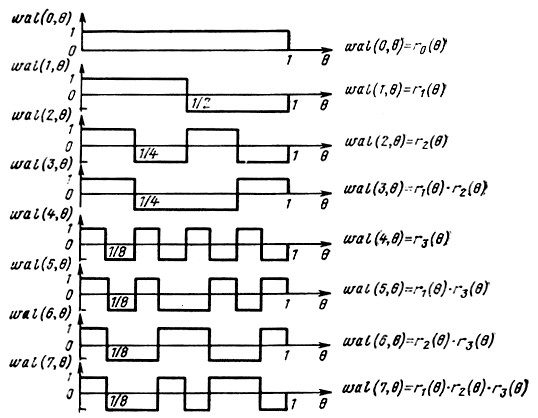
Рис. 9.10. Графики первых восьми функций Уолша