§ 15.2. Метод гармонической линеаризации (частотный метод)

Исходную нелинейную схему, в выходном сигнале которой содержатся высшие гармоники, заменяют эквивалентной линейной схемой с синусоидальной выходной реакцией. Амплитуда и фаза искомой синусоидальной функции зависят от амплитуды входного сигнала, а частота совпадает с частотой входного синусоидального сигнала.

Для получения линейной схемы каждый нелинейный элемент представляют линейным на основании найденной описывающей функции. Нелинейную характеристику элемента аппроксимируют уравнением, связывающим входной и выходной сигналы на нелинейном элементе. После подстановки в аппроксимирующее уравнение входного гармонического сигнала в уравнении отбрасывают слагаемые с высшими гармониками. В результате получают описывающую функцию нелинейного элемента, вид которой зависит от аппроксимирующей характеристики нелинейного элемента. После этого описываемую функцию представляют в комплексной форме. Расчет эквивалентной схемы проводят комплексным методом.

Определение описывающей функции эквивалентной системы. Нелинейную характеристику нелинейного элемента аппроксимируют аналитическим выражением, связывающим входной f₁ и выходной f₂ сигналы: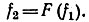

Выражение входного гармонического сигнала 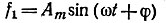подставляют в аналитическое уравнение характеристики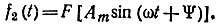

В общем случае выходной сигнал содержит первую и высшую гармоники, амплитуды которых зависят от амплитуды входного сигнала.

В выражении для f₂(t) отбрасывают высшие гармоники и рассматривают эквивалентную схему гармонической линеаризации нелинейного элемента.

Комплексную амплитуду выходной реакции находят по формуле 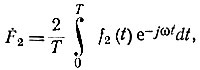либо через изображение по Лапласу 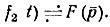[Временная функция, соответствующая изображению по Лапласу, совпадает с заданной f₂(t) в интервале 0 < t < T; f₂ = 0 при t > Т = 2π/ω.]

Таким образом, передаточная функция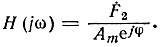

Пример. Найти эквивалентное комплексное сопротивление нелинейной индуктивности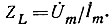

Решение. Вебер-амперная характеристика при небольшом насыщении может быть представлена в виде 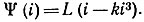Подставим в это выражение искомый ток i = I_mcosωt:

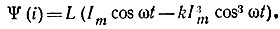
Напряжение на индуктивном элементе

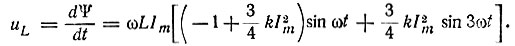
В полученном выражении учтем только первую гармонику (гармоническая линеаризация):

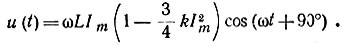
Комплексную амплитуду определим из выражения u(t):

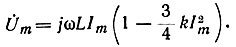
Эквивалентное комплексное сопротивление индуктивного элемента

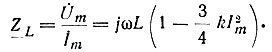
Метод гармонической линеаризации (частотный метод)

Алгоритм метода. 1. Характеристику нелинейного элемента аппроксимируют соответствующим выражением. 2. Находят выражения для комплексных параметров всех нелинейных элементов, включенных в исходную схему, и составляют эквивалентную комплексную схему. 3. В соответствии с комплексной схемой определяют комплексную амплитуду выходного сигнала.

Пример. Методом гармонической линеаризации найти входной ток нелинейного последовательного колебательного контура с нелинейным индуктивным элементом.

Решение. Пусть контур имеет малые потери и на его входе действует синусоидальное напряжение.

Заменим нелинейный индуктивный элемент эквивалентным комплексным сопротивлением: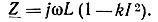

Представим схему контура в виде комплексной схемы замещения (рис. 15.1), для которой запишем комплексное уравнение гармонической линеаризации:

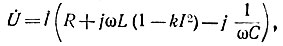
откуда комплексное сопротивление контура

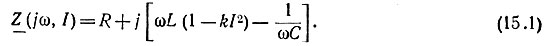
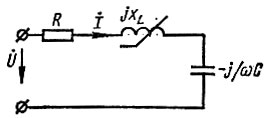
Рис. 15.1

Перейдем к нормированному сопротивлению 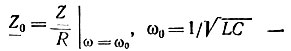резонансная частота.

При малых токах, т. е. на линейном участке, из выражения (15.1) для комплексного нормированного сопротивления имеем

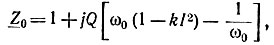
где Q = ω₀L/R - добротность контура.

Найдем зависимость модуля первой гармоники тока от частоты:

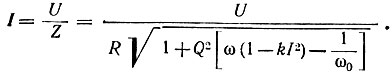
Резонансные кривые I(ω) даны в § 13.15. При малых токах kI² можно пренебречь. В результате получим резонансную кривую линейного контура.