
§ 15.3. Метод гармонического баланса
Метод гармонического баланса предполагает, что решение нелинейного дифференциального уравнения содержит только первую, первую и одну или несколько высших гармоник. При этом неизвестными являются амплитуды гармоник (если фаза э. д. с. источника равна нулю); амплитуды и начальная фаза источника; амплитуды и фазы гармоник и начальная фаза источника.
Трудность метода состоит в решении алгебраических уравнений высших степеней или трансцендентных уравнений.
Алгоритм метода. 1. Характеристику нелинейного элемента для мгновенных значений аппроксимируют соответствующим аналитическим выражением. 2. В аналитическое выражение характеристики, связывающей входные и выходные параметры нелинейного элемента, подставляют предполагаемое решение только для первой гармоники (первой и высшей гармоники). 3. Для исследуемой схемы составляют дифференциальное уравнение, в которое вводят функцию, определяющую нелинейный элемент (см. § 15.2) и предполагаемое решение. Полученное уравнение преобразовывают так, чтобы выделить синусные и косинусные составляющие. 4. Последовательно приравнивают коэффициенты при синусной и косинусной составляющих первой и высших (если они есть) гармоник. Получают два уравнения для определения неизвестных.
Пример. Определить изменение потокосцепления Ψ(i) в нелинейном элементе схемы рис. 15.2 методом гармонического баланса при u = Umsinωt.

Рис. 15.2
Решение. Приближенно представим вебер-амперную характеристику нелинейной индуктивности зависимостью i = aΨ3. Ищем решение для потокосцепления в виде
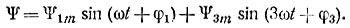
Тогда
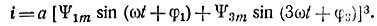
Составим дифференциальное уравнение схемы:
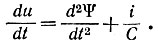
В полученное уравнение подставим выражения для u, Ψ, i:
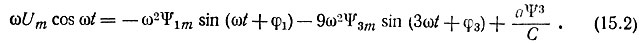
В уравнение (15.2) вместо Ψ3 вводим выражение
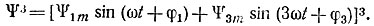
В результате тригонометрических преобразований все члены уравнения (15.2) представим в виде синусных Aksin kωt и косинусных Bkcos kωt составляющих. Приравниваем коэффициенты
при cos ωt:
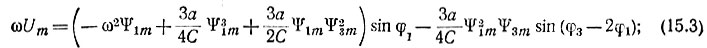
при sin ωt:
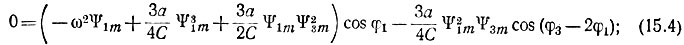
при cos 3ωt:
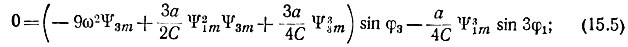
при sin 3ωt:
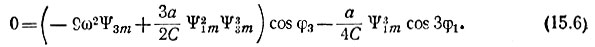
Решаем уравнения (15.3)-(15.6) относительно 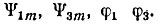

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
