§ 15.4. Метод медленно меняющихся амплитуд

Методом медленно меняющихся амплитуд (метод малого параметра) могут быть приближенно решены нелинейные дифференциальные уравнения второго порядка, в которых нелинейные коэффициенты малы (малый параметр нелинейности) по сравнению с другими коэффициентами уравнения. Это означает, что в такой цепи установившиеся колебания близки к гармоническим.

Данный метод состоит в решении не исходного дифференциального уравнения, а в решении более простых нелинейных уравнений, так называемых укороченных уравнений, не содержащих временных составляющих. Его применяют для приближенного анализа установившегося и переходного режимов автономных^* и неавтономных^** систем.

^* (Автономными называют нелинейные системы, в которых не содержится переменных во времени источников.)

^** (Неавтономными называют нелинейные системы, имеющие переменные во времени источники и описываемые уравнениями, которые содержат в явном виде время.)

Найдем решение уравнения

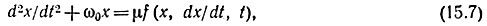
где μ - безразмерный положительный коэффициент, определяющий нелинейность (малый параметр). При μ = 0 уравнение линейно. При μ ≠ 0 зададимся решением в виде

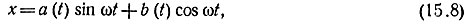
где a(t) и b(t) - медленно меняющиеся функции времени искомого колебания по сравнению с частотой источника ω.

Решение (15.8) подставляют в уравнение (15.7). В левой и правой частях полученного уравнения приравнивают коэффициенты при синусах и косинусах.

Учитывая, что амплитуды во времени изменяются относительно медленно, можно пренебречь первыми da(t)/dt, db(t)/dt и вторыми d²a(t)/dt², d²b(t)/dt² производными по сравнению с другими коэффициентами при синусах и косинусах, В результате получим

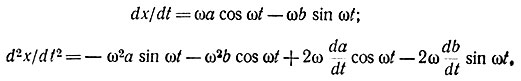
Производные dx/dt и d²x/dt² подставляют в исходное уравнение (157). Правую часть полученного выражения раскладывают в ряд Фурье, после чего сравнивают коэффициенты при одинаковых тригонометрических функциях, В результате образуются два уравнения:

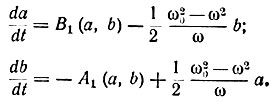
Из этих уравнений определяют амплитуды а(t) и b(t),