§ 17.5. Метод последовательных интервалов

При численном методе последовательных интервалов в дифференциальном уравнении производную dy/dt заменяют отношением конечных приращений Δy/Δt, интеграл 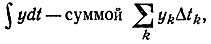время переходного процесса t разбивают на n малых равных интервалов Δt. Полученное приближенное уравнение решают относительно приращения функции:

Приращение искомой функции Δy_k определяют как разность мгновенных значений функции в конце y_k и начале рассматриваемого интервала y_k-1, т. е. по уравнению (17.1) Δy_k = y_k - y_k-1. По характеристике нелинейного элемента y(х) находят значение Δх_k и так от интервала к интервалу. Этот метод приводит к постепенному накоплению ошибки, которая зависит от величины интервала Δt. Решение удобно представить в виде таблицы.

Пример. Методом последовательных интервалов решить уравнение, описывающее переходный процесс в нелинейном индуктивном элементе Ψ(i) при подключении его через резистивный элемент R к источнику напряжения постоянного U.

Решение. Дифференциальное уравнение цепи dΨ/dt = U - Ri приближенно запишем в виде

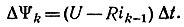
Разобьем промежуток времени переходного процесса на n равных интервалов Δt. Приближенно будем считать длительность переходного процесса до установления конечных значений Ψ₀ и I₀ по постоянной времени τ₀ = Ψ₀/I₀R.

Для k-го интервала

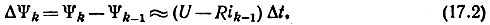
В начале первого интервала (рис. 17.3) при 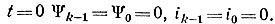Тогда для первого интервала времени по уравнению (17.2)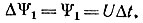

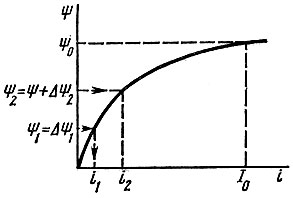
Рис. 17.3

По кривой Ψ(i) для полученного значения ΔΨ₁ найдем ток i₁.

Для второго интервала времени приращение потокосцепления

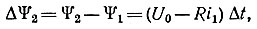
отсюда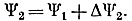

По кривой Ψ(i) для полученного значения определим ток i₂ и т. д.

Расчет удобно свести в таблицу.