§ 17.6. Метод графического интегрирования

Метод графического интегрирования применим к решению нелинейных дифференциальных уравнений первого порядка с разделяющимися переменными, т. е. в основном к нелинейным цепям постоянного тока. Он основан на построении вспомогательной кривой подынтегрального выражения с последующим графическим нахождением площади этой кривой (площади, выраженной определенным интегралом). Кривую подынтегрального выражения строят в функции переменной, по которой проводят интегрирование.

Пример. Определить переходный ток при коротком замыкании в схеме с последовательным соединением нелинейного индуктивного элемента и резистора.

Решение. Дифференциальное уравнение схемы имеет вид

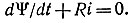
Разделяя переменные и интегрируя полученное уравнение, найдем

где Ψ₀ - значение потокосцепления в момент замыкания ключа.

Уравнение (17.3) решим графически. Для этого построим кривую подынтегрального выражения 1/R_i = f(Ψ) (рис. 17.4), используя характеристику Ψ(i) (см. рис. 17.3). Задаваясь произвольным значением тока i_k, по кривой Ψ(i) найдем Ψ_k. Для определения времени, в течение которого достигается значение потокосцепления Ψ_k, подсчитываем площадь, ограниченную осью Ψ (от 0 до Ψ_k) и кривой Ψ(1/R_i). В результате строим кривую Ψ(t).

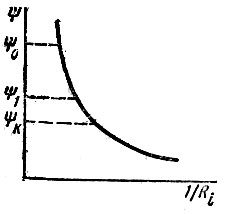
Рис. 17.4