§ 17.7. Метод фазовой плоскости

Метод фазовой плоскости позволяет провести качественное исследование процессов, происходящих главным образом в автономных схемах (линейных и нелинейных) и описываемых дифференциальными уравнениями первого и второго порядка. При этом можно исследовать зависимость переходного процесса от начальных условий, выяснить возможность возникновения резонансов, автоколебаний, неустойчивых состояний и др.

Данный метод основан на построении траекторий движения точки, отображающей состояние системы. В случае схем, содержащих гармонические источники, от уравнений для мгновенных значений функции, характеризующей переходный процесс, переходят к уравнениям для мгновенных значений амплитуд или к уравнениям для медленно меняющихся амплитуд.

Фазовая плоскость образуется декартовой системой координат (рис. 17.5), по одной оси которой откладывают параметр, изменяющийся во времени и характеризующий функцию х(t), а по другой - производную от этой функции: dx/dt = y.

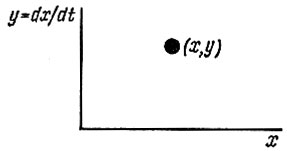
Рис. 17.5

Изображающая точка (x, y) на фазовой плоскости характеризует состояние системы в данный момент. Фазовая траектория - траектория движения изображающей точки.

Уравнения первого порядка характеризуются одной фазовой траекторией (рис. 17.6), уравнения второго порядка - несколькими (рис. 17.7).

Рис. 17.6

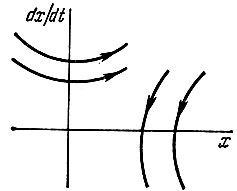
Рис. 17.7

Движение изображающей точки может происходить только по часовой стрелке, в верхней полуплоскости - в сторону увеличения, в нижней - в сторону уменьшения х. Начало движения фазовых траекторий зависит от начальных условий. При различных начальных условиях фазовые траектории не пересекаются.

Периодические процессы характеризуются замкнутыми траекториями. Семейство фазовых траекторий на фазовой плоскости образует фазовый портрет.

Особые точки на фазовой плоскости. Особые точки на фазовой траектории - это точки на фазовой плоскости, в которых dx/dt = dy/dt = 0. Эти точки лежат на оси x и соответствуют условиям равновесия, если построения по фазовой плоскости производят для мгновенных значений.

Особые точки классифицируются по характеру корней характеристического уравнения (по виду фазовых траекторий, окружающих эти точки). Например,

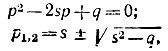
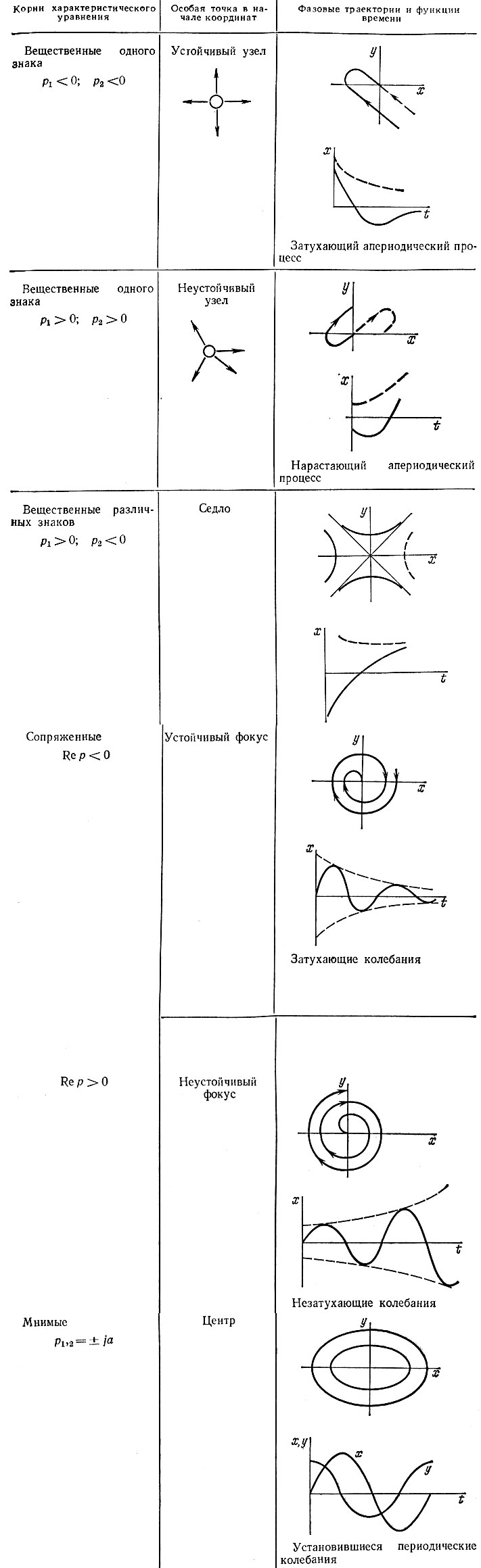
Метод фазовой плоскости

Рассмотрим следующие методы построения фазовых траекторий: метод изоклин; дельта-метод; метод Льенара.

Метод изоклин. Данный метод является наиболее общим методом построения фазовых траекторий. Его применяют при решении любых уравнений второго порядка автономной цепи, он основан на геометрическом представлении производной как наклона касательной к траектории в рассматриваемой точке на фазовой плоскости.

Изоклина - это линия, пересекающая фазовые траектории под одним и тем же углом и являющаяся геометрическим местом точек на фазовой плоскости, для которых dy/dx - постоянное число.

Пример. Построить изоклины для линейного автономного уравнения второго порядка

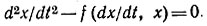
Решение. Преобразуем заданное уравнение в уравнение первого порядка, для которого построить фазовые траектории проще. Введем новую переменную y = dx/dt, тогда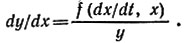

Таким образом, уравнение изоклины имеет вид

Для построения первой изоклины будем считать производную dy/dx равной постоянному числу dy/dx = а₁. Тогда

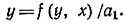
Задаваясь различными значениями x, по уравнению (17,4) найдем соответствующие значения y.

Вторую изоклину строим, полагая dy/dx = a₂ и т. д.

По построенному семейству изоклин строим фазовые траектории y = f(x). Из выбранной точки M (рис. 17.8) проводим прямую Mm под углом к оси х, тангенс которого равен a₁. Прямую Mn проводим под углом к оси x, тангенс которого равен а₂. Соединяем точки тип отрезком прямой. Расстояние mn делим пополам, в результате чего получим точку N. Прямая MN является отрезком фазовой траектории. Построения повторяем до заполнения всей фазовой плоскости.

Дельта-метод. Этот метод применяют в случае, когда требуется построить одну фазовую траекторию. Участки траектории представляют в виде отрезков дуг окружностей с центрами, расположенными на оси x.

Дельта-метод применим к автономным уравнениям вида 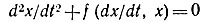и к неавтономным вида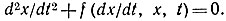

При построении фазовой траектории этим методом исходят из уравнения 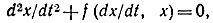в которое вводят (y - x), заменяя dx/dt на y, d²x/dt² на 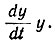В результате получают

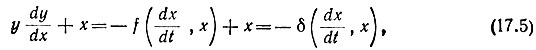
где

Для малых изменений y = dx/dt и x можно считать, что δ постоянная величина. При этом условии уравнение (17.5) решают путем разделения переменных

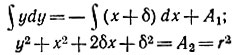
или

При малых приращениях последнее уравнение описывает дугу окружности с центром в точке (y = 0, x = -δ). Дуги окружностей строят следующим образом (рис. 17.9). Для известных начальных условий x(0) и 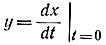по уравнению (17.6) определяют абсциссу центра окружности (-δ). Координаты центра окружности (y = 0, x = -δ₁) подставляют в уравнение (17.7) и находят радиус r₀, которым проводится дуга длиной, например, 01. После этого уточняют длину этой дуги, взяв среднее значение δ_k на участке 01. Затем строят второй участок дуги 1-2 и также уточняют его длину и т. д.

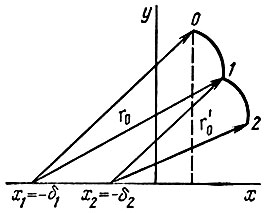
Рис. 17.9

Метод Льенара. Данный метод графически определяет направление фазовой траектории в заданной точке фазовой плоскости. Его применяют при решении уравнений вида d²x/dt² - f(dx/dt) + х = 0, описывающих состояние цепей с линейными реактивными и нелинейными резистивными элементами.

Обозначая 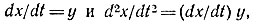получим уравнение изоклины

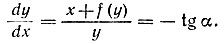
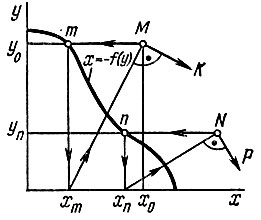
Сначала строят линию нулевой изоклины dy/dx = 0 при x = -f(y) (рис. 17.10). Функция -f(y) пропорциональна в. а. х. нелинейного резистивного элемента. Затем определяют направление траектории в точке М(x₀, y₀), координаты которой являются заданными начальными условиями 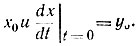Из точки М опускают перпендикуляр на ось ординат. Пересечение перпендикуляра с кривой -f(y) образует точку m с абсциссой x_m. Соединяя точки М и x_m прямой Мx_m и восстанавливая из точки М перпендикуляр к прямой Мх_m, определим направление касательной к фазовой траектории в точке М. Отрезок МК (произвольной, но достаточно малой длины) является отрезком фазовой траектории. Отрезок фазовой траектории, например NP, в точке N находят с помощью аналогичных построений.