2. Двоичная система счисления

До последнего времени во всех вычислениях, производимых в различных отраслях науки и техники, использовалась десятичная система счисления, состоящая из десяти элементарных цифр (символов):

Однако эта система счисления не являлась единственной. Так, например, в известной латинской, или, как ее еще иногда называют, римской, системе в основном используется пять символов:

^* (Иногда в этой системе используют еще два знака:

)

где I = 1, V = 5, X = 10, С = 100 и М = 1000.

Существует также еще ряд систем счисления, но наиболее простой из них является двоичная система. В этой системе имеется только два символа: единица и нуль.

Если в десятичной системе необходимо иметь десять различных сигналов (десять разных значений тока), каждый из которых соответствует одной из десяти используемых цифр, то в двоичной системе необходимо только два различных сигнала. Эти сигналы могут создаваться чрезвычайно просто: "единица" - ток в цепи есть; "нуль" - ток в цепи отсутствует^*. Кроме этого, в двоичной системе очень просты правила сложения и умножения. Благодаря этому двоичная система получила в вычислительной технике и кибернетических системах автоматического управления широкое распространение.

^* (В связи с тем, что в системах автоматического управления широко применяются вакуумные и полупроводниковые приборы, не являющиеся идеальными выключателями, то сигналом "нуль" практически является не отсутствие тока в цепи, а наличие небольшого тока, который легко отличим от тока, принятого за единицу.)

Интересно отметить, что управление в живых организмах также происходит по дискретной двоичной системе.

Нервная клетка (нейрон) находится либо в возбужденном состоянии, либо нет. Чтобы нейрон возбудился, величина раздражения должна достигнуть определенной так называемой пороговой величины. Это явление в физиологии известно под названием закона "все или ничего".

Конечно, двоичная система имеет и недостатки. Главным из них является то, что для записи какого-либо числа в двоичной системе необходимо больше разрядов, нежели в десятичной системе счисления. Кроме того, сама форма записи только при помощи "1" и "0" является очень непривычной. Однако недостатки, которые имеет двоичная система, с лихвой окупаются ее преимуществами.

Прежде чем перейти к рассмотрению двоичной системы, проследим, как записываются числа в десятичной системе. Рассмотрим натуральный ряд чисел, т. е. целые числа, записанные в порядке возрастания:

Вначале числа записываются соответствующими знаками. Однако этих знаков всего десять. Поэтому переход от числа 9 к числу 10 происходит по особому закону. В этом случае последний из имеющихся символов (девять) заменяется на первый символ системы (нуль) и слева записывается следующий символ (единица). Таким образом, число 10 записывается уже при помощи двух разрядов.

Следующее число записывается заменой нуля на единицу (11), затем единица заменяется двойкой (12) и т. д.

Рассмотренный метод перехода к записи следующего числа не зависит от типа системы счисления. Поэтому применим этот метод и к двоичной системе. Как уже говорилось, в этой системе используется только два знака. Для удобства в качестве этих символов выбраны первые две цифры десятичной системы: 0 и 1.

Поэтому "нуль" и "единица" в двоичной системе записываются теми же цифрами, что и в десятичной. Но для того, чтобы записать число "два", в двоичной системе уже нет специального символа. Поэтому для записи этого числа воспользуемся вышеуказанным правилом.

Последний из имеющихся символов (в данном случае "1") заменяется на первый знак системы (нуль) и слева записывается единица. Следовательно, число "два" в двоичной системе записывается в виде "10".

Число "три" образуется заменой нуля на следующий символ, т. е. на единицу: "11".

Число "четыре" образуется по правилу, аналогичному правилу записи числа "два", однако здесь оба символа (единицы) заменяются нулями, а слева добавляется единица: "100".

Далее числа записываются аналогичным образом. В итоге получаем следующую таблицу.

Таблица 1.1. Перевод десятичных чисел в двоичные

Как следует из этой таблицы, в одном разряде (не считая нуля) можно записать только одно двоичное число: "1". Иначе говоря, количество чисел, записываемых в одном разряде, определяется из равенства: 2⁰ = 1. В двух разрядах уже можно записать три (2⁰ + 2¹ = 3) числа: "01, 10, 11", в трех разрядах - семь (2⁰ + 2¹ + 2² = 7) чисел: "001, 010, 011, 100, 101, 110, 111", и т. д. Поэтому в R разрядах можно записать следующее количество чисел:

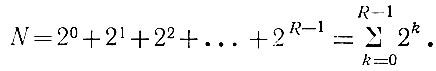(1.1)

Легко увидеть, что ряд 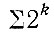представляет собой геометрическую прогрессию со знаменателем q = 2 и первым членом а₁ = 2⁰ = 1. Пользуясь уравнениями геометрической прогрессии, можно определить сумму R членов этого ряда:

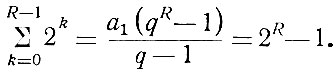
Следовательно, в R разрядах можно записать

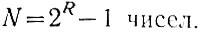(1.2)

Из этого равенства определяется число разрядов, необходимых для записи в двоичной системе счисления числа N:

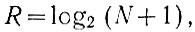(1.3)

где log₂ N - логарифм числа N при основании, равном двум.

Пример. Определить, сколько необходимо иметь разрядов в двоичной системе для записи тридцати одного числа (N = 31).

Используя уравнение (1.3), получаем

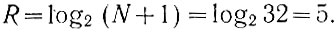
Следовательно, для записи 31 числа необходимо 5 двоичных разрядов.

Необходимо иметь в виду, что при выполнении расчетов по уравнению (1.3) число разрядов не всегда получается целым. В таком случае результат должен быть округлен до следующего наибольшего целого числа. При этом следует иметь в виду, что в полученном (округленном) числе разрядов (R) может быть записано более N чисел.

Пример. Пусть N = 20. Тогда из уравнения (1.3) следует, что

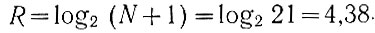
Округляя результат, получаем

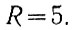
Однако (ур. 1.2) в пяти разрядах можно записать:

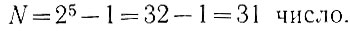
Таким образом, для записи двадцати чисел необходимо иметь пять разрядов, но в этих пяти разрядах всего можно записать тридцать одно число (более двадцати чисел).

Следует отметить, что в справочниках таблицы логарифмов с основанием два обычно отсутствуют. Однако, пользуясь известными приемами пересчета, можно использовать любые другие имеющиеся таблицы.

Действительно, равенство N = 2^х может быть записано в следующем виде:

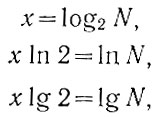
где ln N - натуральный логарифм числа N.

lg N - десятичный логарифм числа N.

Исключая из этих уравнений неизвестное х, получаем

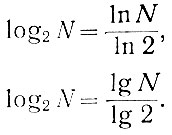
Подставляя в эти уравнения значения логарифмов ln 2 и lg 2, определяем необходимые зависимости

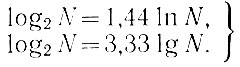(1.4)

По способу записи запятой двоичные системы делятся на две части:

а) система с фиксированной запятой

В этом случае двоичное число, например

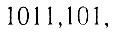
имеет в нужном месте запятую, которая вообще не кодируется. Целая часть числа в этом случае записывается в одних специально для этого выделенных разрядах, а дробная часть - в других разрядах.

б) система с плавающей запятой

В этой системе число (N) представляется в виде двух частей: мантиссы и порядка.

Так, например, 101,01 = 0,10101 ⋅ 10¹¹,

где 10 - число "2" в двоичной системе,

11 - число "3" в этой же системе.

Поэтому в системе с плавающей запятой отдельно шифруется мантисса (в данном примере 10101) и отдельно - порядок (здесь 11).

Знаки мантиссы и порядка кодируются в виде