
3. Перевод двоичных чисел в десятичные
Для того чтобы осуществить перевод двоичной системы счисления в десятичную, необходимо знать, чему равна в десятичной системе каждая единица двоичного числа.
Если двоичное число имеет один (нулевой) разряд, то единица, находящаяся в нем, равна единице десятичной системы (табл. 1.1). Этот пересчет определяется из условия 1 ⋅ 20 = 1. Если единица отсутствует, т. е. в нулевом разряде имеется "нуль", то аналогично получаем 0 ⋅ 20 = 0. Следовательно, в десятичной системе также записывается нуль. Легко увидеть (табл. 1.1), что это правило можно распространить на любой m-ый разряд двоичного числа:
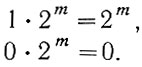 (1.5)
(1.5)Так, например, единица во втором разряде (m = 2) равна (табл. 1.1)
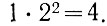
Сказанное позволяет определить правило, по которому осуществляется перевод двоичного числа в десятичное. Этот перевод осуществляется при помощи ряда (ур. 1.1), в котором перед его членами поставлены единицы и нули в соответствии с заданным двоичным числом.
Пример. Перевести в десятичную систему двоичное число 100110.
Записываем ряд (ур. 1.1), который в данном случае имеет 6 членов, ибо заданное число имеет 6 разрядов (нулевой, первый ... пятый):
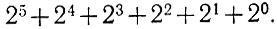
Расставляем в соответствующих разрядах нули и единицы. Поскольку в нулевом, третьем и четвертом разрядах числа 100110, имеются нули, а в остальных единицы, то получаем
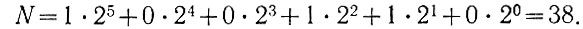

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
