
4. Перевод десятичных чисел в двоичные
Любое десятичное число (N) может быть записано (ур. 1.1) в виде следующего ряда:
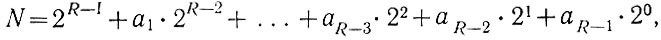 (1.6)
(1.6)где R - число разрядов, необходимых для записи числа в двоичной системе (ур. 1.3);
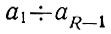 - коэффициенты, равные 0 или 1.
- коэффициенты, равные 0 или 1.
Поэтому первый способ преобразования десятичного числа в двоичное заключается в следующем. Заданное десятичное число необходимо разложить в ряд вида Σ 2m и определить степени (m), которые имеются в этом разложении. Далее нужно в разрядах, равных этим степеням, поставить единицы, а в остальных разрядах записать нули.
Пример. Перевести в двоичную систему число 43.
Раскладываем число 43 в ряд по степеням "2":
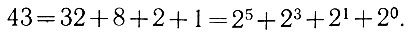
Следовательно, в нулевом, первом, третьем и пятом разрядах двоичного числа будут единицы, а во втором и четвертом разрядах - нули. В итоге получаем
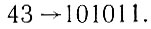
Существует также другой, более простой, способ перевода десятичных чисел в двоичные. Его сущность заключается в следующем. Поделим на два обе части уравнения (1.6). Тогда, учитывая, что 20 = 1, получим
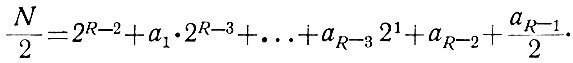 (1.7)
(1.7)Как видим, в результате деления получились целое число (2R-2 + а1 ⋅ 2R-3 + ... + aR-3 21 + аR-2) и остаток (aR-1), причем остаток равен единице в том случае, когда aR-1 = 1. Если же aR-1 = 0, то остаток отсутствует.
Следовательно, если при делении N на два частное является целым числом, то aR-1 = 0; если же после деления в остатке осталась единица, то аR-1 = 1.
Аналогичным образом, поделив 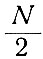 еще раз на два (отбросив при этом член
еще раз на два (отбросив при этом член 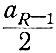 ), можно определить коэффициент aR-2 и т. д.
), можно определить коэффициент aR-2 и т. д.
Из сказанного вытекает следующее правило преобразования десятичного числа в двоичное.
Заданное десятичное число необходимо разделить пополам. Если в результате деления получилось целое число (без остатка), то в нулевом разряде двоичного числа записывается нуль. В том же случае, когда при делении в остатке осталась единица, то в нулевом разряде записывается единица. Далее полученное частное (остаток при этом отбрасывается) вновь делится пополам. Если это деление происходит без остатка, то в первом разряде записывается нуль, если же при этом в остатке получается единица, то в первом разряде ставится единица. Этот процесс продолжается до тех пор, пока частное от очередного деления окажется равным нулю.
Практически этим способом пользуются следующим образом. Заданное десятичное число необходимое количество раз делится на два, а остаток от каждого деления (нуль или единица) записывается рядом в столбик. Этот столбик и представляет собой полученное двоичное число.
Пример. Необходимо преобразовать в двоичную систему число 69. Делим 69 пополам. Получается 34 и в остатке единица. Записываем остаток в правый столбик, а 34 вновь делим на два... Этот процесс продолжается до тех пор, пока в частном не получится нуль. Процесс этого преобразования показан ниже:

Следовательно,
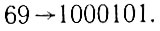

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
