5. Квантование непрерывных сигналов

В технических устройствах часто приходится иметь дело с непрерывными процессами. В этом случае сигналы, передающие информацию об изменении параметров этих процессов, также являются непрерывными.

Казалось бы, что при превращении непрерывных сигналов в дискретные (квантовании) происходит потеря части информации, передаваемой непрерывным сигналом. Однако это не так. В. А. Котельников доказал, что можно так осуществить квантование непрерывных сигналов, что при этом не будет происходить потеря информации.

Доказательство теоремы Котельникова основывается на следующем. Во-первых, любой сигнал, передаваемый по реальному проводу (каналу), имеет ограниченный частотный спектр. Это происходит потому, что при проходе через реальный аппарат, например через обмотку возбуждения электрической машины, сигнал сглаживается и высшие гармоники тока становятся настолько малыми, что ими можно пренебречь. Во-вторых, в сигнале всегда содержатся помехи, искажающие его. Поэтому передача сигнала с ошибкой, меньшей, чем величина помех, практически соответствует передаче его без ошибки.

Следовательно, непрерывная функция со спектром, ограниченным сверху частотой f_max, может быть точно представлена конечным числом ее значений, определяемых с интервалом времени, не более (рис. 1.2)

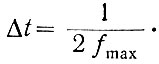(1.8)

Благодаря этому появляется возможность преобразования непрерывного сигнала в дискретный без потери информации.