Глава II. Электронные логические схемы

1. Основные понятия алгебры логики

Логика является наукой о формах и законах мышления. Логика подразделяется на диалектическую и формальную.

Формальная логика описывает формы мышления как постоянные, неизменные. Диалектическая логика является учением о развитии форм и законов мышления. Поэтому основным фактором диалектической логики, отличающим ее от формальной, является фактор развития; развитие же обусловливается противоречиями, составляющими основу каждого явления.

Диалектическая логика находится еще только в стадии формирования. Формальная логика является наукой, исследованной в значительно большей степени.

Одна из отраслей формальной логики, развивающаяся применительно к потребностям математики, называется математической логикой. Одним из разделов математической логики является алгебра логики или Булева алгебра. Последнее название алгебра логики получила по имени одного из ее основателей - Д. Буля. Буль положил начало разработке логического исчисления, позволяющего оперировать с логическими суждениями так же, как это делается в элементарной математике с алгебраическими символами, которые можно складывать, умножать, и т. д.

Обозначим буквой А какое-либо сообщение, которое в математике принято называть высказыванием. Каждое высказывание может быть либо истинным (правильным), либо ложным (неверным). Примем, что истинность высказывания будет обозначаться словом "ДА", а ложность высказывания - словом "НЕТ". Если при этом для передачи высказывания использовать двоичный код, то его истинность будет передаваться сигналом "1", а ложность - сигналом "0".

Так, например, пусть буквой А обозначено высказывание (сообщение) "Катушка включена". Тогда истинность этого высказывания обозначается равенством А = 1. В случае же, когда это высказывание ложно, можно записать: А = 0.

Математический аппарат алгебры логики позволяет решать два типа задач:

а) задачи анализа, когда, имея электронную (или электромеханическую) схему, необходимо описать ее при помощи логических операций;

б) задачи синтеза, когда необходимо построить электронную машину (электромеханический аппарат) по заданной логической схеме.

Любое сложное высказывание состоит из простых. Поэтому при помощи простых высказываний можно построить сложное, которое может быть либо истинным, либо ложным. Благодаря этому на базе нескольких простейших электронных или электромеханических элементов представляется возможным синтезировать любые сложные логические высказывания.

Рассмотрим основные связи между простыми высказываниями.

а) Отрицание высказывания

Эта операция обозначается символом 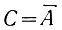и читается: "Выказывание С истинно тогда, когда не истинно (ложно) высказывание А". Поскольку высказывание обозначается символами "1" или "0", то для операции отрицания высказывания получаем следующие равенства:

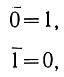(2.1)

т. е. отрицание нуля равно единице, а отрицание единицы есть нуль.

В электронных схемах логический элемент, осуществляющий отрицание, обозначается (рис. 2.1) прямоугольником, на котором написано слово "НЕ" или "НЕТ". Стрелка, направленная к прямоугольнику, показывает вход элемента, а другая стрелка - выход элемента. Сигнал на выходе элемента (1) имеется тогда, когда нет сигнала (0) на его входе. Когда же на вход элемента подан сигнал, то на его выходе сигнал отсутствует.

Рис. 2.1. Схематическое изображение электронного логического элемента, выполняющего операцию отрицания

б) Конъюнкция двух высказываний

Конъюнкция высказываний обозначается символами С = А ∧ В или С = А ⋅ В и читается: "Высказывание С истинно в том случае, если истинны высказывания А и В".

Знак "точка" используется здесь в связи с тем, что конъюнкция определяет таблицу логического умножения двух чисел (для двоичной системы):

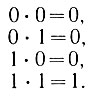(2.2)

Логический элемент, при помощи которого выполняется конъюнкция, обозначается прямоугольником (рис. 2.2) с надписью "И". Естественно, что поскольку этот элемент выполняет сравнение двух высказываний (А и В), то он имеет два входа. Импульс на его выходе (С = 1) появляется в том случае, когда истинны высказывания А и В, т. е. когда А = 1 и В = 1. Иначе говоря, импульс на выходе элемента будет только в том случае, когда имеются сигналы на обоих его входах.

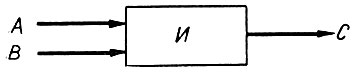
Рис. 2.2. Логический элемент, производящий конъюнкцию двух высказываний

В случае, когда элемент выполняет конъюнкцию n высказываний, он, естественно, имеет n входов.

в) Дизъюнкция двух высказываний

Дизъюнкция высказываний обозначается либо символом С = А ∇ В, либо С = А + В и читается: "Высказывание С истинно тогда, когда истинно высказывание А или В".

При помощи дизъюнкции производятся операции логического сложения двух двоичных чисел:

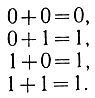(2.3)

Логический элемент, выполняющий дизъюнкцию высказываний, обозначается прямоугольником с надписью "ИЛИ" (рис. 2.3). Напряжение на выходе этого элемента появляется тогда, когда подан сигнал на один из его входов: А или В. При дизъюнкции n высказываний элемент имеет n входов.

Рис. 2.3. Логический элемент, выполняющий дизъюнкцию двух высказываний

Более сложные высказывания могут быть выражены при помощи отрицания, конъюнкции и дизъюнкции.

Так, например, высказывание С = АВ, но B = D + E записывается в виде

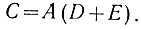
В соответствии с этим в электрических схемах сложное логическое высказывание выполняется на основе простейших элементов "НЕ", "И" и "ИЛИ".

Для рассмотренного выше примера логическое высказывание выполняется при помощи двух логических элементов (рис. 2.4). Первый элемент (ИЛИ) выполняет дизъюнкцию высказываний (D + E), а второй (И) - конъюнкцию A (D + E).

Рис. 2.4. Схема, выполняющая логическое действие 'А (D + Е)'

Следует иметь в виду, что операции отрицания, конъюнкции и дизъюнкции не являются независимыми. Они связаны между собой следующими уравнениями:

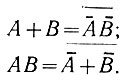(2.44)

Черточка над двумя буквами обозначает отрицание логического произведения или суммы.

Доказываются равенства (ур. 2.4) достаточно просто. Символы А и В в отличие от аналогичных знаков в элементарной алгебре не могут иметь любые значения, а равны только либо единице, либо нулю. Поэтому, если рассмотреть равенства (2.4) для четырех возможных случаев

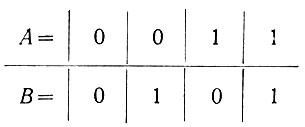(2.5)

то, учитывая правила логического умножения (ур. 2.2) и сложения (2.3), нетрудно убедиться в их справедливости.

Следует отметить, что число типов электронных или электромеханических элементов, при помощи которых можно выполнить любое сложное высказывание, может быть сведено к одному.

Рассмотрим логический элемент типа "И-НЕ" (этот элемент часто обозначают буквой "L"), который выполняет следующее логическое высказывание (операцию Шеффера):

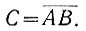
Имея элементы типа "И-НЕ", можно построить схемы, выполняющие операции отрицания, дизъюнкции и конъюнкции (рис. 2.5). Доказательства этого утверждения нетрудно получить, рассматривая все возможные (усл. 2.5) значения высказываний А и В.

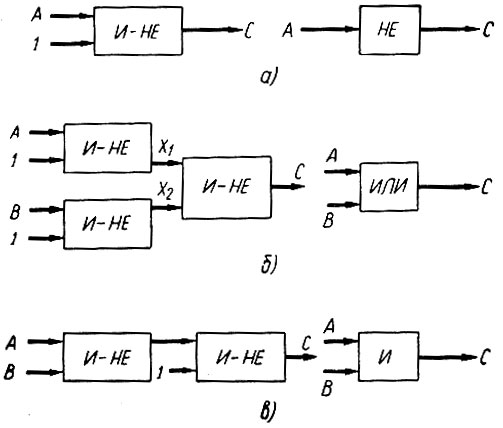
Рис. 2.5. Схемы выполнения логических операций отрицания (а), дизъюнкции (б) и конъюнкции (в) при помощи элементов типа 'И-НЕ'

В качестве примера доказательства рассмотрим схему дизъюнкции (рис. 2.5, б). Обозначив выходы первых двух элементов типа "И-НЕ" через Х₁ и Х₂, получаем:

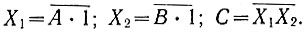
Результаты этих преобразований для любых возможных значений А и В сведены в табл. 2.1.

Таблица 2.1. Логические преобразования, выполняемые схемой рис. 2.5, б

Сравнивая полученные результаты с правилами логического сложения (ур. 2.3), легко убедиться в том, что схема рис. 2.5, б выполняет дизъюнкцию высказывании.

В последнее время получил распространение еще один элемент, при помощи которого могут быть получены любые другие логические элементы. Этот элемент, обозначаемый на схемах прямоугольником с надписью "ИЛИ-НЕ" (рис. 2.6), выполняет следующую логическую операцию:

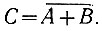
Рис. 2.6. Схематическое изображение логического элемента 'ИЛИ-НЕ'

Пользуясь способом, рассмотренным для схем рис. 2.5, легко показать, как при помощи логического элемента "ИЛИ-НЕ" можно выполнить логические операции "НЕ", "ИЛИ" и "И" (рис. 2.7).

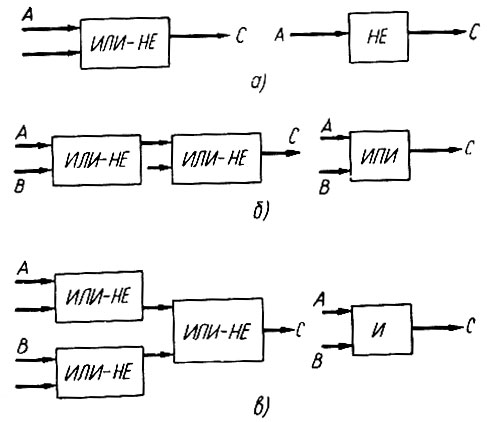
Рис. 2.7. Схемы выполнения операций 'НЕ', 'ИЛИ' и 'И' при помощи логических элементов типа 'ИЛИ-НЕ'

Следует отметить, что элементы типа "И-НЕ" и "ИЛИ-НЕ" обычно не используются для замены рассмотренных выше трех типов логических элементов. Однако в ряде случаев некоторые сложные высказывания могут быть реализованы проще при помощи этих элементов, нежели элементов типа "НЕ", "ИЛИ", "И".

Уравнения алгебры логики можно также преобразовывать, как это делается в элементарной математике с формулами алгебраического сложения и умножения. Эти преобразования имеют следующий вид:

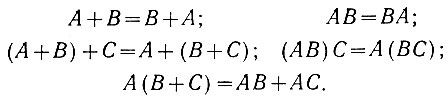
Поскольку символы (А, В и т. д.) в алгебре логики могут быть равными только 0 или 1, то при проведении преобразований необходимо иметь в виду, что могут появиться равенства, не свойственные элементарной алгебре. Примером таких равенств являются следующие:

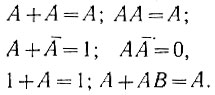(2.6)

Доказываются равенства (2.6) таким же путем, как и равенства (2.4).

Поэтому следует помнить, что аналогия между логическим и обычным алгебраическим сложением и умножением является неполной. Если, например, в элементарной алгебре можно записать, что А + А = 2А, то в алгебре логики (ур. 2.6) А + А = А.

Кроме того, в алгебре логики есть действия (например, операция отрицания), которые не имеют прямого аналога в элементарной алгебре.

Пользуясь правилами алгебры логики, можно исследовать возможности упрощения имеющихся логических выражений.

Пример. Необходимо разработать схему, выполняющую следующее сложное логическое преобразование (суждение):

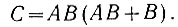
Легко увидеть, что это действие выполняется при помощи трех блоков (рис. 2.8, а). Однако заданное логическое преобразование может быть значительно упрощено. Рассмотрим возможность этого упрощения:

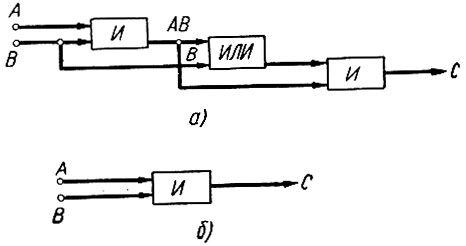
Рис. 2.8. Две схемы, выполняющие одно и то же логическое преобразование

Но, как следует из равенства (2.6),

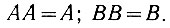
Поэтому

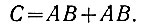
Кроме того (ур. 2.6), D + D = D. Следовательно, обозначив D = AB, получаем

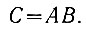
Таким образом, рассматриваемое логическое преобразование может быть выполнено только одним логическим элементом (рис. 2.8, б).