2. Арифметические действия в двоичной системе

Основываясь на правилах логического умножения и сложения, можно при помощи рассмотренных выше логических электронных элементов создать устройства, выполняющие операции сложения, вычитания, умножения и деления.

а) Сложение двоичных чисел

Сложение двоичных чисел осуществляется по правилам логического сложения (ур. 2.3). Однако при этом необходимо иметь в виду, что единица, получающаяся при сложении двух единиц, переносится (прибавляется) в более высокий разряд. Поэтому для сложения двух одноразрядных чисел получаем следующие правила:

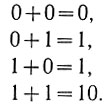(2.7)

Эти правила могут быть реализованы в схеме, показанной на рис. 2.9, которая составляется следующим образом.

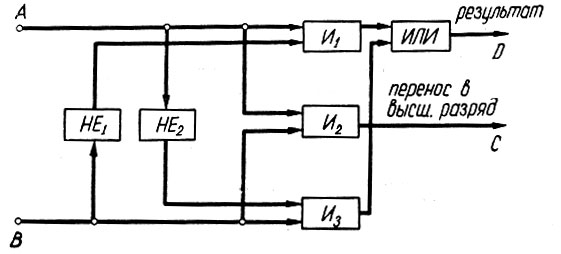
Рис. 2.9. Схема сложения двух чисел

Прежде всего, сигнал переноса (С), как это следует из четвертого равенства (ур. 2.7), имеет место тогда, когда оба слагаемых (А и В) равны единице. Это логическое высказывание можно записать в виде

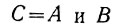
или

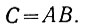
Поэтому сигнал переноса является выходом логического элемента "И₂", на входы которого поданы сигналы А и В (рис. 2.9).

Единица в том же разряде получается (ур. 2.7) в двух случаях, когда

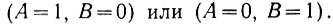
Используя терминологию алгебры логики, эти условия можно записать в следующем виде:

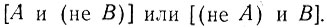
Введение условных обозначений логических операций упрощает данную запись:

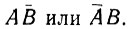
Это сложное логическое выражение в конечном виде можно записать следующим образом:

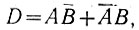(2.8)

где D - сигнал результата сложения.

Рассматриваемое логическое преобразование может быть выполнено (рис. 2.9) при помощи пяти логических элементов: "HE₁", "HE₂", "И₁", "И₃" и "ИЛИ".

Однако для нахождения результата сложения (D) уравнение (2.8) не является оптимальным (в отношении количества используемых логических элементов). Это происходит потому, что в нем не используется уже имеющийся сигнал переноса С = АВ. Проведенные в этом отношении исследования показывают следующее.

Учитывая, что АА‾ = 0 и ВВ‾ = 0 (ур. 2.6), запишем уравнение (2.8) в следующем виде:

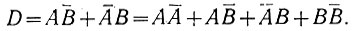
После несложных преобразований получаем:

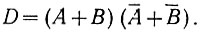
Как следует из второго уравнения (2.4),

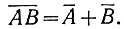
Следовательно,

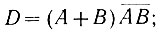
но

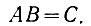
Таким образом, в окончательном виде

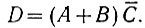
Данное логическое высказывание проще, чем высказывание (ур. 2.8). Поэтому сложение выполняется (рис. 2.10) при помощи четырех (а не шести, как в предыдущем случае) логических элементов.

Схемы рис. 2.9 или 2.10 используются лишь при сложении одноразрядных чисел. Для того чтобы сложить два R-разрядных числа, необходимо иметь сумматор, состоящий из одноразрядных сумматоров (ОС). Схема такого сумматора на три разряда показана на рис. 2.11.

Рис. 2.10. Упрощенная схема сложения

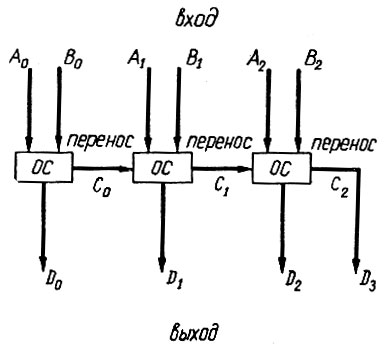
Рис. 2.11. Сумматор на три разряда

На вход этого устройства подаются два трехразрядных числа (A₂A₁A₀ и B₂B₁B₀). На выходе получается четырехразрядное число (D₃D₂D₁D₀).

Как следует из этой схемы, каждый одноразрядный сумматор (ОС) должен быть выполнен таким образом, чтобы он мог складывать три одноразрядных числа: А, В и перенос с низшего разряда (С). Одна из схем такого сумматора, выполненная на логических элементах типа "НЕ", "ИЛИ", "И", показана на рис. 2.12.

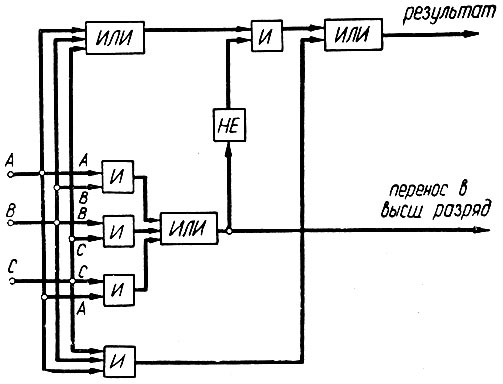
Рис. 2.12. Сумматор на три одноразрядных числа

б) Вычитание двоичных чисел

Вычитание двоичных чисел может быть выполнено двумя методами.

Прежде всего можно сконструировать устройство, которое, вычитая меньшее число из большего, в каждом разряде выполняет непосредственно вычитание по правилам:

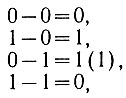(2.9)

где единица в скобках обозначает перенос (добавление) в высший разряд вычитаемого числа.

Пользуясь этими правилами, легко построить логическую схему, выполняющую вычитание двух одноразрядных чисел.

Обозначим уменьшаемое число буквой А, а вычитаемое - В. Тогда сигнал переноса (С) появляется в том случае, когда

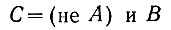
или

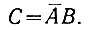
Это логическое высказывание выполняется (рис. 2.13) при помощи двух логических элементов (НЕ₂ и И₂).

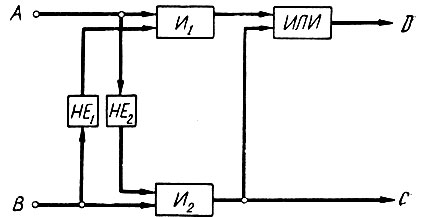
Рис. 2.13. Логическая схема вычитания двух одноразрядных чисел

В результате вычитания единица в том же разряде получается в случае, когда А = 1 и В = 0 или А = 0 и В = 1. Это логическое высказывание, как было показано при рассмотрении операций логического сложения, записывается в следующем виде:

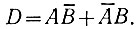
Данное высказывание (рис. 2.13) выполняется пятью логическими элементами, два из которых одновременно используются для получения сигнала переноса (С).

Сравнивая схемы сложения (рис. 2.9) и вычитания (рис. 2.13) одноразрядных чисел, легко увидеть, что они отличаются друг от друга только логикой определения сигнала переноса.

Часто бывает очень удобным на одной и той же схеме выполнять как сложение, так и вычитание. В этом случае операция вычитания специальным приемом сводится к сложению. Делается это следующим образом.

Рассмотрим вычитание двух R-разрядных чисел:

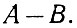
Нормализуем большее из этих двух чисел, т. е. запишем его в следующем виде:

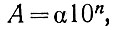
где α - мантисса двоичного числа (число, меньшее единицы, но имеющее единицу после запятой),

n - порядок числа,

10 - число "два", записанное в двоичной системе.

Пример нормализации двоичного числа:

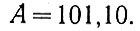
Записывая это число в таком виде, чтобы целая часть отсутствовала и после запятой была единица, получаем:

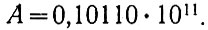
Запишем теперь меньшее из рассматриваемых чисел (В) в следующем виде:

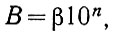
где n равно показателю нормализованного числа А.

Тогда получим следующее равенство:

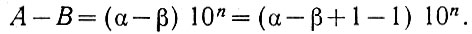(2.10)

Введем далее новое число (δ), которое равно

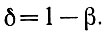
Из этого равенства следует, что

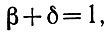(2.11)

т. е. δ дополняет β до единицы. Поэтому δ называется дополнительным числом числа β.

Дополнительное число в двоичной системе получается заменой всех нулей (справа от запятой) на единицы, а единиц - на нули и прибавлением в низший разряд единицы. В правильности сказанного нетрудно убедиться, прибавив полученное этим способом дополнительное число (δ) к исходному (β) и получив при этом (ур. 2.11) единицу.

Подставив значение β (ур. 2.11) в уравнение (2.10), получаем

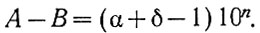(2.12)

Сравнивая уравнения (2.10) и (2.12), можно записать:

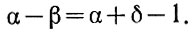
Таким образом, для того чтобы вычесть два числа, необходимо к уменьшаемому прибавить число, дополнительное к вычитаемому, и от полученного результата вычесть единицу. Благодаря этому вычитание двух чисел сводится к операции сложения.

Рассмотрим примеры вычитания двух чисел при помощи логических операций сложения (ур. 2.7).

Пример 1. А = 1000 (восемь), В = 101 (пять).

Определить А - В (уменьшаемое больше вычитаемого).

1. Нормализуем большее число:

А = 0,1 ⋅ 10¹⁰⁰, т. е. α = 0,1000.

2. Выравнивая порядок чисел А и В (n = 100), получаем:

В = 0,0101 ⋅ 10¹⁰⁰, т. е. β = 0,0101.

3. Находим число, дополнительное к β:

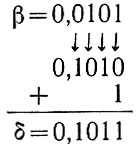
4. Складываем α + δ:

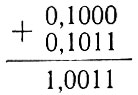
5. Вычитаем из полученной суммы единицу (α + δ - 1):

Таким образом,

Пример 2. А = 110 (шесть), В = 1011 (одиннадцать).

Определить А - В (уменьшаемое меньше вычитаемого).

1. Нормализуем большее число:

В = 0,1011 ⋅ 10¹⁰⁰, т. е. β = 0,1011.

2. Выравнивая порядок (n = 100) чисел А и В, получаем:

А = 0,011 ⋅ 10¹⁰⁰, т. е. α = 0,0110.

3. Находим число, дополнительное к β:

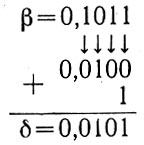
4. Складываем α + δ:

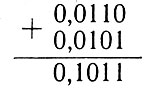
5. Вычитаем единицу:

Поскольку в результате вычитания получается отрицательное число, запишем его в следующем виде:

Как было показано выше, вычитание двух чисел, расположенных в круглой скобке, можно свести к операции сложения. Для этого необходимо к уменьшаемому (единице) прибавить число, дополнительное к вычитаемому (0,1011), и из полученного результата вычесть единицу.

Следовательно, α + δ - 1 равно числу, дополнительному к 0,1011, взятому со знаком минус.

6. Определяем число, дополнительное к 0,1011:

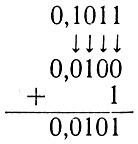
Поэтому

в) Умножение двоичных чисел

Умножение одноразрядных чисел выполняется в соответствии с правилами логического умножения (ур. 2.2). Как следует из этих правил, умножение одноразрядных чисел выполняется при помощи логического элемента "И".

Умножение R-разрядных чисел производится так же, как и в элементарной алгебре, и сводится к операциям сложения и сдвига.

Пример. Перемножить числа 101 (пять) и 1011 (одиннадцать).

Умножение выполняется следующим образом:

г) Деление двоичных чисел

Поскольку двоичные одноразрядные числа имеют только два значения (0 и 1), то правила их деления чрезвычайно просты:

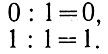(2.13)

Деление R-разрядных чисел выполняется так же, как и в элементарной алгебре, и сводится к операциям вычитания.

Пример. Разделить 110111 (пятьдесят пять) на 101 (пять).

Деление происходит следующим образом: