
5. Методика расчета кодирующей матрицы
Числа, кодируемые диодной матрицей, могут записываться в виде нормального ряда (подряд): 1, 10, 11, 100 и т. д. Однако часто с целью экономии количества используемых в матрице диодов числа, имеющие наибольшее количество единиц (диодов) пропускаются. В первом случае матрица называется нормально заполненной, во втором случае - матрицей с пропусками чисел.
Рассмотрим вначале нормально заполненную матрицу.
а) Общее число диодов в матрице
Прежде всего необходимо обратить внимание на то, что R-разрядное число имеет R знаков, причем в высшем разряде всегда стоит единица. Так, например, трехразрядными (R = 3) являются следующие числа:
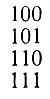 (2.14)
(2.14)В то же время такие числа, как например 010 или 011, хотя и имеют три знака, но являются двухразрядными. Нуль впереди этих чисел записывается для удобства их сравнения с трехразрядными числами. Вместе с этим следует иметь в виду, что в R разрядах можно записать числа, имеющие не только R, но и менее разрядов. Так, например, в трех разрядах могут быть записаны двух- и одноразрядные числа:

Как было показано ранее (ур. 1.1), количество чисел, записываемых в R разрядах, определяется рядом:
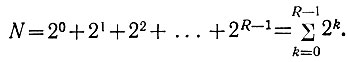
Поэтому в R разрядах содержится следующее количество R-разрядных чисел:
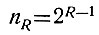 (2.15)
(2.15)Пример. Сколько имеется трехразрядных чисел
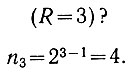
Рассмотрим структуру R-разрядного числа (например, 2.14). В высшем разряде все числа имеют диоды (единицы), а в каждом из остальных разрядов только половина чисел имеет диоды. Поэтому количество диодов, имеющихся в R-разрядном числе, определится (ур. 2.15) из уравнения
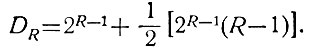
После несложных преобразований получаем более простое выражение
 (2.16)
(2.16)Поскольку в R разрядах записываются все числа, имеющие и более низкие разряды, то общее число диодов в R-разрядной матрице определится равенством
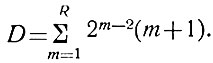 (2.17)
(2.17)Пример. Определить количество диодов, необходимых для четырехразрядной матрицы (R = 4).
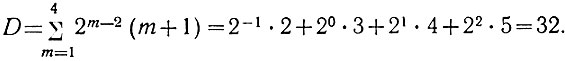
б) Количество R-разрядных чисел, имеющих одинаковое число диодов
В R-разрядной матрице могут быть числа, записанные при помощи 1, 2, 3 ... R диодов. В общем случае обозначим число диодов буквой х. Естественно, что всегда должно соблюдаться неравенство:
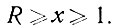 (2.18)
(2.18)Рассмотрим методику определения количества чисел, имеющих одинаковое число диодов, на примере четырехразрядных чисел. Всего существует восемь четырехразрядных чисел:
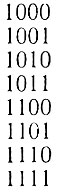
Запишем эти числа в несколько ином порядке и разделим на четыре группы:

Рассмотрение этих групп показывает, что среди R-разрядных чисел есть только одно число, имеющее R диодов, и одно число с одним диодом:
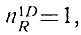 (2.19)
(2.19)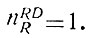 (2.20)
(2.20)Вторая и третья группы, если отбросить единицу в высшем разряде, образуются методом перестановок одного или двух диодов в трех разрядах. Обобщая, можно сказать, что эти числа получаются методом перестановок от одного до R - 2 диодов и в R - 1 разрядах.
Теорема сочетаний, известная из элементарной алгебры, гласит, что число всех сочетаний из n элементов по m определяется равенством
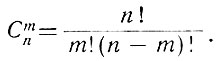
Поэтому количество чисел, имеющих х диодов, равно
 (2.21)
(2.21)Круглая скобка, расположенная справа, как это принято в технической литературе, обозначает, что уравнение верно для всех значений х, меньших R, но больших единицы. В знаменателе этого уравнения стоит х - 1, так как один диод, стоящий в высшем разряде, в определении числа перестановок не участвует. Поскольку вместе с этим диодом в перестановках не фигурирует и высший разряд, то число разрядов в числителе уравнения (2.21) берется на единицу меньше (R - 1).
Пример. Определить количество пятиразрядных (R = 5) чисел, имеющих по 1, 2, 3, 4 и 5 диодов.
Количество чисел, имеющих 1 и 5 диодов, определяется уравнениями (2.19) и (2.20). Числа же, содержащие 2, 3 и 4 диода, подсчитываются по уравнению (2.21):
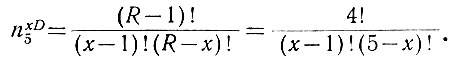
Таким образом, получаем

в) Общее количество чисел, имеющих х диодов в R разрядах
Ранее уже говорилось о том, что в R разрядах можно записать не только R-разрядные числа, но и числа всех меньших разрядов.
Прежде всего (ур. 2.20) следует отметить, что R диодов имеет одно число, содержащее только единицы:
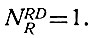 (2.22)
(2.22)R-разрядное число имеет (ур. 2.19) одно число с одним диодом. R-1-разрядное число также имеет одно число с одним диодом и т. д. Поэтому в R разрядах будет следующее количество чисел с одним диодом:
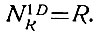 (2.23)
(2.23)Рассмотрим теперь случаи, когда R >> x > 1.
Количество R-разрядных чисел, имеющих х диодов, определяется уравнением (2.21):
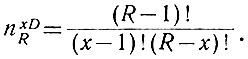
Аналогично этому среди R-1-разрядных чисел х диодов имеют:

Так же можно определить количество чисел, имеющих меньшее число разрядов:
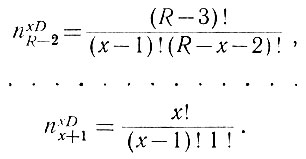
Поэтому общее количество чисел, имеющих х диодов, определится уравнением
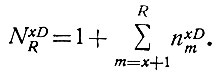 (2.24)
(2.24)В правой части этого уравнения добавляется единица, потому что Σn определяет количество чисел, получающихся методом перестановок. Кроме того, всегда будет еще одно число, содержащее х диодов. Это число, в котором имеются одни единицы (без нулей).
Необходимо также иметь в виду, что наименьший разряд, где есть числа с х диодами, определяется равенством
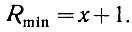
Это обусловлено тем, что всегда имеется только одно число (ур. 2.22), в котором количество диодов равно числу разрядов (R = x). Наличие этого числа уже учтено в уравнении (2.24) единицей, добавленной к Σn.
Подставив в уравнение (2.24) значения nmxD, получаем
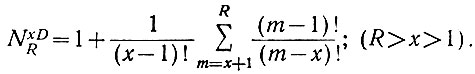 (2.25)
(2.25)Рассмотрим три частных случая этого уравнения. Подставив в уравнение (2.25) x = R - 1, R - 2 и R - 3, после несложных преобразований получаем
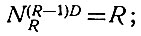 (2.26)
(2.26)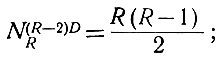 (2.27)
(2.27)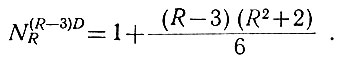 (2.28)
(2.28)Аналогично могут быть получены зависимости и для более низких разрядов.
Пример. Определить, сколько чисел в семи разрядах (R = 7) имеют 6, 5 и 4 диода.
Как следует из уравнения (2.26), шесть (R - 1 = 6) диодов имеют 7 чисел. Подставляя значение R = 7 в уравнения (2.27) и (2.28), определяем, что 5 диодов имеет 21 число, а 4 диода - 35 чисел.
г) Матрица с одним лишним разрядом
Иногда бывает целесообразно добавить в матрицу лишний разряд, чтобы не записывать в ней числа с наибольшим количеством диодов. Этим достигается определенная экономия диодов.
Выше было показано (ур. 1.3), что количество разрядов, необходимых для записи N чисел подряд, определяется уравнением
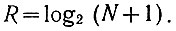
Для упрощения изложения примем, что полученное значение R - целое число.
Добавим к матрице еще один разряд
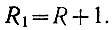
Благодаря добавлению одного разряда количество чисел, которые могут быть записаны в матрице, увеличится (ур. 1.1) на
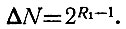 (2.29)
(2.29)Значит, из матрицы может быть изъято ΔN чисел, имеющих наибольшее количество диодов.
Максимальное количество диодов (R) имеет (ур. 2.22) только одно число. R - 1 диодов имеет NR(R-1)D чисел, R - 2 диодов - NR(R-2)D чисел и т. д. Поскольку общее количество чисел, которые могут быть выброшены (ур. 2.29), равно 2R1-1, получаем
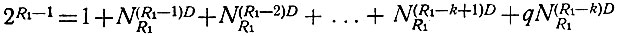
или
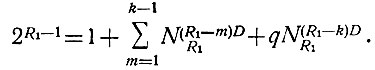 (2.30)
(2.30)Это уравнение показывает, в каком порядке выбрасывается 2R1-1 чисел. Вначале выбрасывается одно число, имеющее R1 диодов. Затем выбрасываются все числа с R1 - 1 диодами (NR1(R1-1)D), далее - с R1 - 2 диодами и т. д. Однако последняя группа чисел, имеющих R1 - k диодов, не всегда может быть выброшена полностью. Поэтому в данной группе выбрасывается только часть (q) чисел. Коэффициенты k и q выбираются так, чтобы левая часть уравнения (2.30) была равна правой части.
Добавление одного разряда к матрице при записи всех чисел подряд увеличивает количество диодов, имеющихся в матрице, на (ур. 2.16)
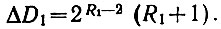 (2.31)
(2.31)Вместе с тем пропуск 2R1-1 чисел, имеющих наибольшее число диодов, позволяет (ур. 2.30) выбросить ΔD2 диодов:
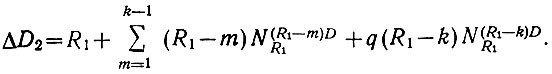 (2.32)
(2.32)Поэтому сэкономленное количество диодов равно
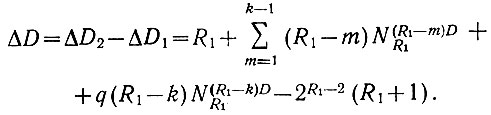 (2.33)
(2.33)Пример. 31 число записывается (подряд) в (ур. 1.3)
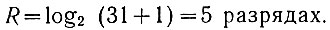
Определить, какое количество диодов можно сэкономить, добавив к матрице еще один разряд (R1 = R + 1 = 6).
1. Определяем коэффициенты k и q:
а) левая часть уравнения (2.30) равна
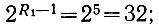
б) члены правой части уравнения определяются из уравнений (2.26)-(2.28);
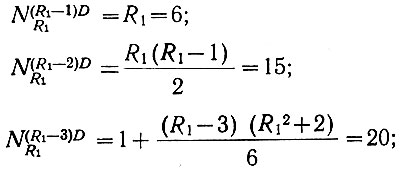
в) приравниваем левую и правую части уравнения (2.30):
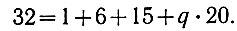
Следовательно, k = 3; q = 0,5.
2. Подсчитываем экономию диодов (ур. 2.33):
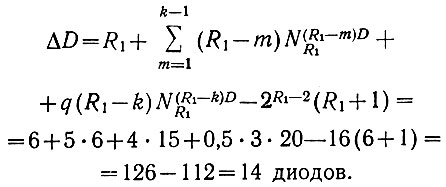
Общее количество диодов в R-разрядной матрице (ур. 2.17)

Поэтому сэкономлено
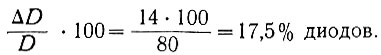

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
