9. Математические действия с непрерывно изменяющимися напряжениями

Большинство схем, используемых для выполнения вычислений с непрерывными напряжениями, основаны на применении электронных усилителей. Такие усилители чаще всего выполняются на полупроводниковых или вакуумных триодах (рис. 2.69). Для сокращения записи далее будем любой из этих усилителей обозначать в виде прямоугольника со стрелкой, показывающей направление действия усилителя (рис. 2.70). Эти усилители увеличивают в k раз подаваемое на их вход напряжение (u) и одновременно с этим (рис. 2.69) меняют (переворачивают) его полярность. Часто в схемах вычисления требуется очень высокий (10⁶ и выше) коэффициент усиления, и для его получения включают последовательно несколько (обычно три) усилителей. В этом случае каскад усилителей также обозначается прямоугольником, показанным на рис. 2.70.

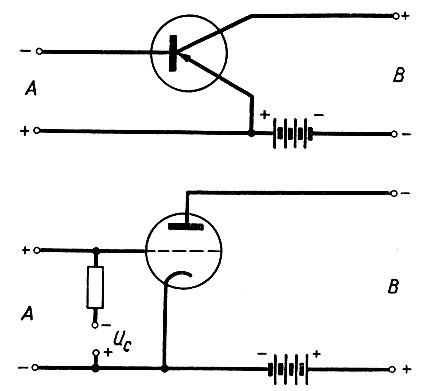
Рис. 2.69. Электронные усилители на полупроводниковых и вакуумных триодах

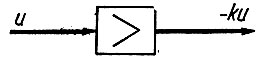
Рис. 2.70. Схематическое изображение усилителя

Рассмотрим, каким образом выполняются различные операции с непрерывно изменяющимися напряжениями.

а) Масштабное звено

Для получения наибольшей точности работы любой схемы вычисления необходимо, чтобы максимальные напряжения, подаваемые на схему, были по возможности ближе к номинальным для этой схемы значениям. Однако максимальные напряжения, с которыми приходится иметь дело, могут иметь самые различные величины. Использовать же для изменения этих напряжений усилители (рис. 2.69) нельзя, ибо они имеют постоянный коэффициент усиления.

Поэтому в схемах вычисления обычно используются масштабные звенья, позволяющие легко осуществлять плавное регулирование коэффициента усиления. Схема масштабного звена показана на рис. 2.71. Определим коэффициент усиления этой схемы:

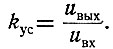
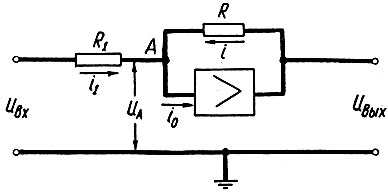
Рис. 2.71. Схема масштабного звена

Поскольку ток i₀ (ток сетки лампы или базы транзистора) во много раз меньше токов i₁ и i, то пренебрежем им, т. е. примем, что i₀ = 0. Поэтому для схемы рис. 2.71 можно записать следующие зависимости:

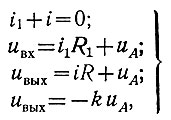(2.44)

где k - коэффициент усиления усилителя.

Решая совместно уравнения (2.44), получаем

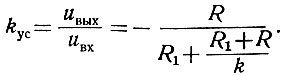
Как было показано выше, коэффициент усиления усилителя (k) обычно очень велик. Поэтому, приняв его бесконечно большим (k = ∞), получаем

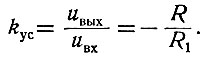(2.45)

Таким образом, коэффициент усиления масштабного звена можно регулировать путем изменения величин сопротивлений R или R₁.

б) Сложение напряжений

Рассмотрим схему, показанную на рис. 2.72. Как и ранее, примем, что i₀ = 0. Тогда для этой схемы можно записать:

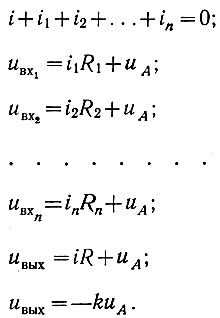
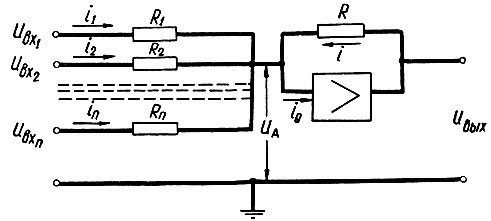
Рис. 2.72. Схема сумматора

Решая эти уравнения совместно, получаем

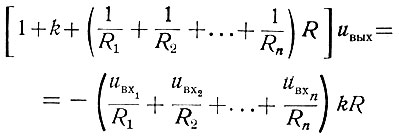
или

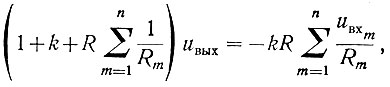
откуда определяем

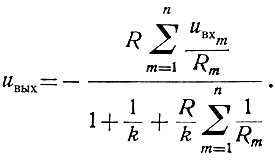
Приняв k = ∞, получаем следующую зависимость:

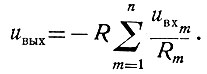(2.46)

Если принять, что R = R₁ = R₂ = ... = R_n, то

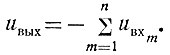(2.47)

Таким образом, схема, показанная на рис. 2.72, позволяет осуществлять сложение любого необходимого количества напряжений. Поэтому схема рис. 2.72 называется сумматором.

в) Вычитание напряжений

Вычитание легко свести к операции сложения:

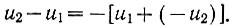
Поэтому (рис. 2.73) уменьшаемое напряжение (u₂) необходимо подать на масштабное звено с коэффициентом усиления, равным единице (R₁ = R). Масштабное звено изменит знак вычитаемого напряжения. После этого необходимо произвести сложение двух напряжений на сумматоре.

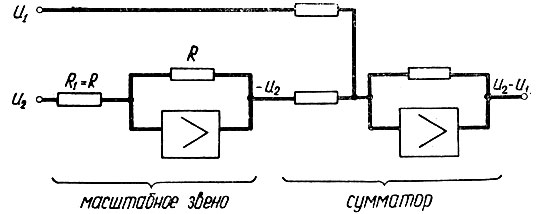
Рис. 2.73. Схема вычитания двух напряжений

г) Интегрирование напряжения

Интегрирование напряжения осуществляется по схеме, показанной на рис. 2.74.

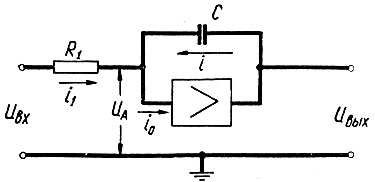
Рис. 2.74. Схема интегрирования напряжения

Действительно, если пренебречь током i₀, то для этой схемы можно записать:

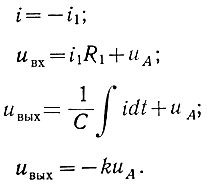
Решая эти уравнения, получаем

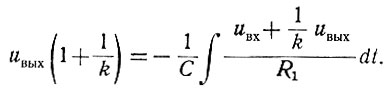
Приняв, что k = ∞, записываем:

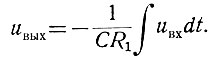(2.48)

Интегрирование далеко не всегда производится при нулевых начальных условиях. Поэтому в схемах интегрирования должны быть предусмотрены специальные цепи для введения этих условий.

Введение начального условия производится зарядом конденсатора до заданной величины напряжения. Причем, как правило, в интегрирующем блоке нельзя выключать конденсатор из цепи обратной связи усилителя, так как это может привести к большой ошибке при решении из-за нестабильности характеристик усилителя с отключенной обратной связью. Поэтому заряд конденсатора осуществляется от внешнего источника напряжения (u_С) по схеме, показанной на рис. 2.75. В схеме верхнее положение переключателя соответствует введению начального условия, а нижнее - рабочему состоянию схемы.

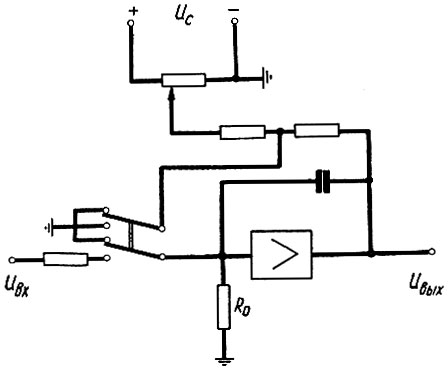
Рис. 2.75. Схема введения начального условия

д) Дифференцирование напряжения

Дифференцирование напряжения производится по схеме рис. 2.76. Для этой схемы (i₀ = 0) имеют место следующие зависимости:

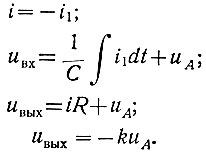
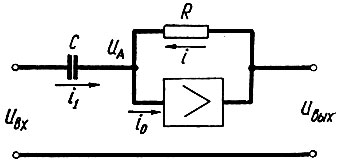
Рис. 2.76. Схема дифференцирования напряжения

Решая эти уравнения совместно, получаем:

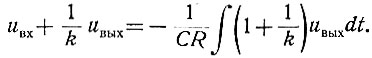
Приняв, что k = ∞, получаем

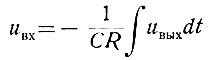
или

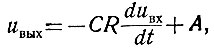(2.49)

где А - постоянная величина, определяемая дополнительными условиями.

Операция дифференцирования в отличие от интегрирования имеет серьезные недостатки, заключающиеся в том, что

а) дифференциатор (рис. 2.76) усиливает высокочастотные помехи, увеличивая ошибку дифференцирования;

б) повышенная чувствительность схемы к высокочастотным генерациям может привести к появлению в ней незатухающих высокочастотных колебаний.

В связи с этим к операции дифференцирования прибегают только в крайнем случае. В том случае, когда это возможно, необходимо понизить порядок уравнения, избежав процесса дифференцирования.

Так, например, необходимо определить ток из уравнения

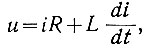
где R и L - постоянные величины.

Проинтегрировав обе части уравнения, получаем

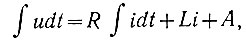
где А - постоянная интегрирования.

В данном случае операция дифференцирования заменяется интегрированием (порядок решения подобных уравнений будет показан в конце этой главы).

е) Блоки переменных коэффициентов

В случае, когда в процессе вычислений необходимо определенным образом изменять (во времени) какой-либо коэффициент уравнения, для этой цели используются блоки переменных коэффициентов.

Блок переменного коэффициента создается при помощи программного переключателя. Переключатель через заданный промежуток времени (Δt) переключается на следующую позицию, включая различные напряжения, которые (рис. 2.77) подбираются так, чтобы в наилучшей степени аппроксимировать заданную характеристику изменения коэффициента a во времени (прерывистая кривая).

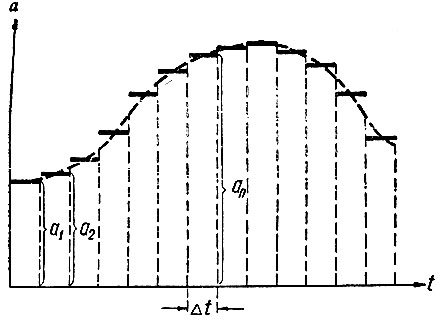
Рис. 2.77. Определение напряжений, задаваемых блоком переменных коэффициентов

ж) Нелинейные блоки

При необходимости введения в выполняемый расчет нелинейной функции u_вых = f(u_вх), заданной графически, используются нелинейные блоки.

Для того чтобы представить функцию в нелинейном блоке, необходимо аппроксимировать ее при помощи отрезков прямых линий (рис. 2.78) и найти параметры аппроксимации а₂, а₃ ... и b₁, b₂, b₃ ...

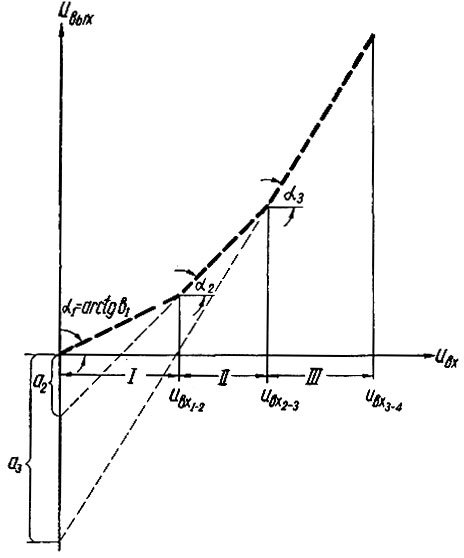
Рис. 2.78. Линейно-кусочная аппроксимация функции

Наиболее простая схема нелинейного блока показана на рис. 2.79. В этой схеме имеется несколько цепей, каждая из которых соответствует определенному участку аппроксимируемой функции. Так, например, цепь, в которую включено сопротивление R₁, соответствует первому (I) участку функции (рис. 2.78); цепь с R₂ и е₂ - второму (II) участку и т. д. Переключение из одной цепи в другую осуществляется переключателем, работающим в зависимости от величины напряжения на входе блока: если u_вх ≤ u_вх1-2 (рис. 2.78), то переключатель находится в первом положении; при u_вх2-3 ≥ u_вх ≥ u_вх1-2 переключатель включается во вторую цепь и т. д.

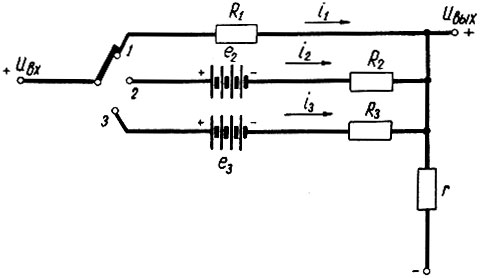
Рис. 2.79. Схема нелинейного блока с переключателем

Определим параметры цепей нелинейного блока, осуществляющего линейно-кусочную аппроксимацию функции.

Для n-го положения переключателя (рис. 2.79) можно записать:

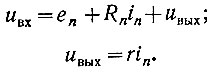
Решая уравнения совместно, получаем

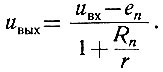
С другой стороны, для n-го участка аппроксимирующей прямой (рис. 2.78) следует, что

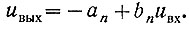(2.51)

Решая совместно уравнения (2.50) и (2.51), получаем

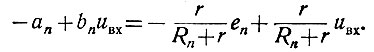
Поэтому параметры n-ой цепи нелинейного блока определяются зависимостями

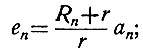(2.52)

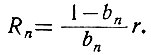(2.53)

Величина сопротивления r выбирается произвольно, однако она должна быть значительно меньше, чем величины сопротивлений R₁, R₂ ...

Рассмотренная схема нелинейного блока имеет переключатель, работающий в зависимости от величины напряжения на входе. Этот переключатель может быть заменен обычными полупроводниковыми диодами.

Так, например, на рис. 2.80 показан блок, состоящий из трех цепей сопротивлений - R₁, R₂ и R₃. Аналогично может быть создан нелинейный блок на любое другое количество цепей. Число этих цепей определяется необходимым количеством участков аппроксимации (рис. 2.78).

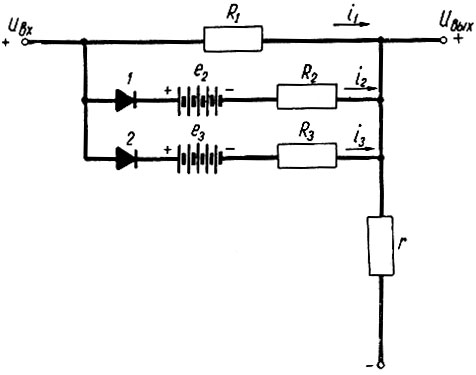
Рис. 2.80. Схема бесконтактного нелинейного блока

Схема, показанная на рис. 2.80, работает следующим образом. Если напряжение на входе относительно мало (u_вх ≤ u_вх1-2 рис. 2.78), то имеющиеся в цепях нелинейного блока э. д. с. (е₂ и е₃) запирают вентили, и ток проходит только по цепи, образуемой сопротивлением R₁. Когда напряжение u_вх превысит величину u_вх1-2, вентиль 1 отпирается, и ток проходит уже по двум цепям (по цепям сопротивлений R₁ и R₂). После того как напряжение достигнет u_вх2-3 открывается вентиль 2, и ток уже идет по трем цепям.

Параметры цепей нелинейного блока определяются следующим образом.

Для случая, когда u_вх ≤ u_вх1-2, можно записать:

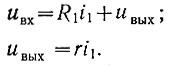
Следовательно,

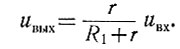
Выберем величину сопротивления r настолько малой, чтобы ею по сравнению с другими сопротивлениями нелинейного блока можно было пренебречь. Тогда запишем:

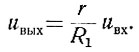
Как следует из рис. 2.78, для первого участка

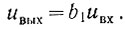(2.54)

Поэтому из двух последних уравнений определяем

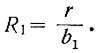(2.55)

В случае, когда u_вх2-3 ≥ u_вх ≥ u_вх1-2, для нелинейного блока имеют место следующие зависимости (пренебрегаем величиной r по сравнению с другими сопротивлениями):

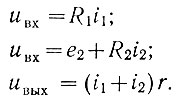
Решая эти уравнения совместно, получаем

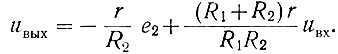(2.56)

На втором участке (рис. 2.78) аппроксимирующая кривая описывается зависимостью

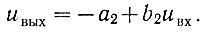
Приравнивая почленно правые части двух последних уравнений, определяем параметры:

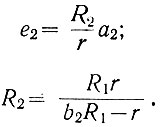
Решая эти уравнения совместно с уравнением (2.55), получаем

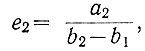(2.57)

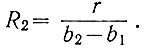(2.58)

Как следует из рассмотренных уравнений, при аппроксимации необходимо, чтобы b₂ > b₁. Это условие (рис. 2.78) всегда выполняется.

Ранее говорилось о том, что цепь 1 вентиля (рис. 2.80) должна открываться при условии

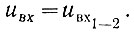
Следовательно, должно иметь место следующее равенство (величиной сопротивления r пренебрегаем):

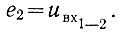(2.59)

Проверим, удовлетворяется ли это равенство при выборе параметров схемы по уравнениям (2.55), (2.57) и (2.58).

Как следует из уравнения (2.54),

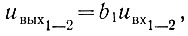
где u_вых1-2 - напряжение на выходе, соответствующее напряжению на входе, равному u_вх1-2

С другой стороны (ур. 2.56),

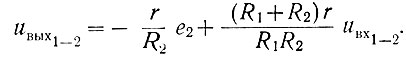
Исключая из двух последних уравнений u_вых1-2, определяем, входное напряжение:

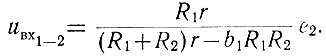
Подставив в это уравнение значения R₁ (ур. 2.55) и R₂ (ур. 2.58), получаем

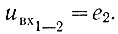
Следовательно, условие (2.59) выполняется.

Аналогично определяются параметры третьей цепи нелинейного блока (рис. 2.80). Поскольку сопротивление r выбирается очень малым и напряжение на нем получается небольшим, та выход нелинейного блока всегда включается на усилитель.

з) Умножение двух напряжений

Умножение выполняется сведением этой операции к сложению и возведению в квадрат. Это преобразование основано на равенстве

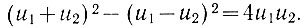(2.60)

Чтобы убедиться в справедливости этого равенства, достаточна раскрыть скобки в его левой части.

Поэтому умножение двух напряжений (u₁ и u₂) выполняется по схеме, показанной на рис. 2.81. Работает схема следующим образом.

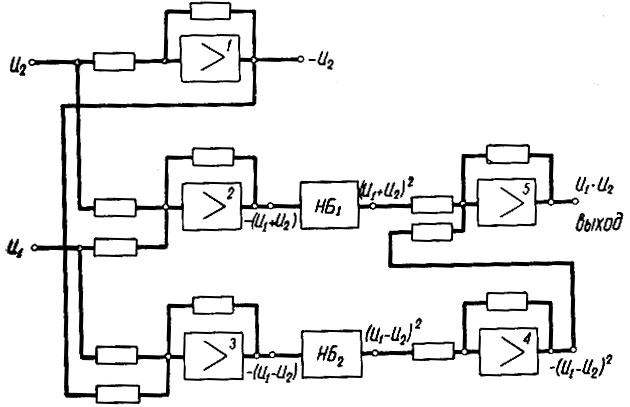
Рис. 2.81. Схема умножения двух напряжений

Усилитель 2 складывает напряжения (u₁ + u₂) и одновременно, как все усилители, меняет знак этой суммы. Усилитель 1 меняет знак напряжения u₂; поэтому на выходе усилителя 3 получается разница напряжений (u₁ - u₂) с обратным знаком. На обоих нелинейных блоках (НБ) при помощи отрезков прямых набирается квадратичная зависимость: u_вых = u²_вх. Поэтому на выходах этих блоков получаются, соответственно, квадраты суммы и разности напряжений. Усилитель 4 меняет знак квадрата разности напряжений, а усилитель 5, осуществляя сложение [(u₁ + u₂)²] + [-(u₁ - u₂)²] и меняя масштаб суммы (уменьшая ее в четыре раза), дает на выходе (ур. 2.60) произведение двух напряжений.

и) Деление двух напряжений

Деление двух напряжений сводится к их умножению вида:

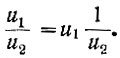
Получение члена ¹/_u2 осуществляется при помощи нелинейного блока, в котором заложена функция

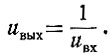
В заключение рассмотрим пример вычисления тока в цепи, схема которой показана на рис. 2.82. Для упрощения изложения рассмотрим процесс, имеющий нулевые начальные условия: необходимо определить кривую тока i = f(t) после включения рубильника.

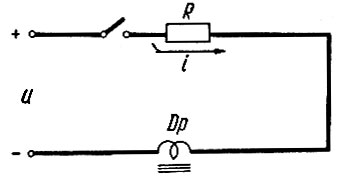
Рис. 2.82. Схема нелинейной цепи, состоящей из сопротивления и дросселя

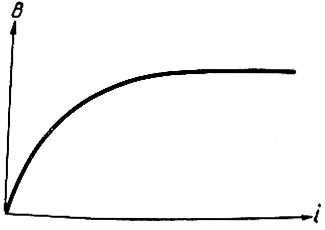
Рис. 2.82. Схема нелинейной цепи, состоящей из сопротивления и дросселя

Рассматриваемая цепь описывается уравнением

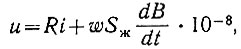(2.61)

где

w - число витков дросселя;

S_ж - поперечное сечение магнитопровода дросселя;

В - индукция в дросселе.

При этом зависимость индукции дросселя от его тока является нелинейной и задана графически (рис. 2.82).

Первоначальное рассмотрение уравнения (2.61) приводит к мысли о необходимости в выполнении операции дифференцирования. Однако, как указывалось ранее, операции дифференцирования необходимо всячески избегать из-за больших погрешностей, вносимых ею.

Попытаемся определить ток цепи, не прибегая к операции дифференцирования. Для этого запишем уравнение (2.61) в следующем виде:

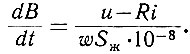(2.62)

Введем обозначения

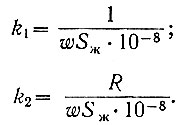
Тогда уравнение (2.62) примет более простой вид:

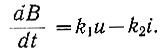(2.63)

Блок-схема решения этого уравнения показана на рис. 2.83. Эта схема строится следующим образом.

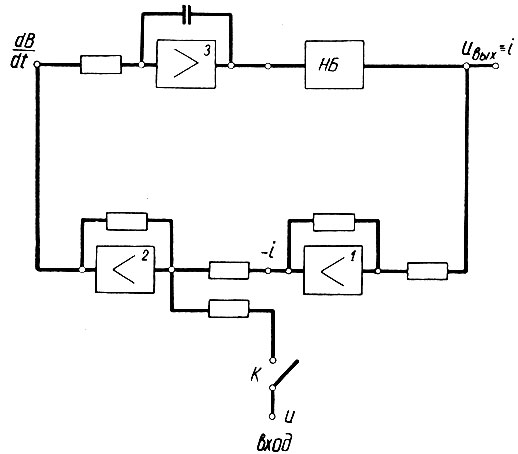
Рис. 2.83. Блок-схема вычисления тока

Как следует из уравнения (2.63), производная индукции 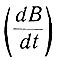равна разности напряжения и тока цепи, умноженных на соответствующие коэффициенты, или, как говорят, взятых в другом масштабе. Примем вначале, что напряжение (u) и ток (i) нам заданы (напряжение действительно задано, но ток необходимо определить).

Тогда подадим "известный" ток (точнее - напряжение, пропорциональное этому току) на вход усилителя 1, который изменит его знак. Далее на вход усилителя 2 подаем напряжение (u) и ток с обратным знаком (-i). Поэтому усилитель 2 выполняет вычитание тока из напряжения. Одновременно (перед вычитанием) подбором величин сопротивлений, установленных на входе этого усилителя, изменяем необходимым образом масштабы напряжения и тока. Следовательно, на выходе усилителя 2 получается напряжение (u = k₁u - k₂i), равное (ур. 2.63) производной 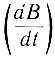. Подавая производную на интегрирующий блок (3), определяем индукцию (В). В свою очередь, индукция попадает на нелинейный блок, в котором заложена заданная графически функция i = φ(-В). Поэтому на выходе получаем искомое значение тока (i). Этот ток подаем на вход усилителя 1.

Если на вход полученной схемы включить при помощи рубильника напряжение (u), то на ее выходе получится искомая кривая i = f(t).

Как следует из рассмотренного примера, отдельные операции вычисления сводятся к созданию электронной модели рассматриваемой электрической цепи. Поэтому операции вычисления, выполняемые при помощи рассмотренных выше элементов, обычно называют моделированием.