
Глава III. Введение в теорию вероятностей и элементы теории информации
1. Основные положения теории вероятностей
Поведение любой электрической системы при произвольных воздействиях на нее является результатом физических закономерностей, присущих системе. Однако эти закономерности, в особенности в кибернетических системах, бывают настолько сложны, что их математическое описание при помощи дифференциальных уравнений становится практически либо невозможным, либо нецелесообразным. В этом случае удобно рассматривать процессы, происходящие в системе, как случайные.
Исследование закономерностей, присущих случайным процессам, происходящим в системах, и является предметом теории вероятностей.
Основным понятием, которым оперирует теория вероятностей, является случайная величина - величина, которая может принимать одно из различных значений, причем заранее неизвестно - какое. Если эти значения образуют непрерывную зависимость, то случайная величина называется непрерывной. В противоположность этому дискретная случайная величина может принимать только отдельные значения.
Любое из значений случайной величины можно рассматривать как случайное событие, которое в процессе наблюдения за ним может либо произойти, либо нет.
Пример. Пусть имеется напряжение, которое получается случайным включением одного, двух или трех аккумуляторов, напряжение каждого из которых равно 2 в. Следовательно, мы имеем дело со случайной величиной (напряжением), возможные значения которой равны 2, 4 и 6 в. Появление же одного из этих напряжений, например 6 в, может рассматриваться как случайное событие.
Количественной оценкой любого случайного события является вероятность его появления.
Теория вероятностей не дает возможности предопределения единичного случайного события. Однако, если в результате многочисленных измерений выяснить закономерности, присущие случайной величине, то становится возможным определение вероятности появления и случайного события.
Пример. Из Риги на взморье отправляется электропоезд. Спрашивается, какое расстояние он пройдет (без остановок), затратив k квт-ч электроэнергии?
Естественно, что это расстояние зависит от того, как машинист ведет поезд, каково напряжение в контактном проводе, сколько пассажиров едет в поезде и т. д. Поэтому определить расстояние, которое пройдет поезд, впервые двигающийся по этому участку, невозможно. Это расстояние является случайной величиной. Однако, если каждый раз записывать расстояние, пройденное поездом, то, пользуясь законами теории вероятностей, можно определить вероятность того, что поезд окажется на заранее заданном участке пути, израсходовав k квт-ч.
Определение вероятности случайного события может быть осуществлено либо изучением особенностей исследуемого события, либо путем обработки опытных данных, полученных в результате серии проведенных опытов. Рассмотрим эти методы на простейших примерах.
Возьмем игральный кубик, на гранях которого написаны цифры от 1 до 6, и будем бросать его на горизонтальную плоскость. В результате такого бросания наверху окажется грань кубика с одной из шести написанных на нем цифр. То, какая грань окажется наверху, зависит от силы броска кубика, величины возникающего при этом броске крутящего момента и множества других факторов, учесть которые заранее невозможно. Поэтому появление на верхней грани кубика какой-либо определенной цифры является случайным событием.
Вероятность появления этого события можно определить, исходя из следующего. Если масса кубика однородна и кубик имеет правильную форму, то появление сверху каждой из шести цифр имеет одинаковую вероятность. Поэтому, приняв вероятность бросания кубика равной единице, легко определить, что вероятность появления одной заранее заданной цифры, например 3, равна
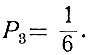
Многократное наблюдение одного и того же случайного события показывает, что ему присущи некоторые устойчивые закономерности. Так, например, проведем N измерений (опытов), в результате которых рассматриваемое событие появилось n раз. Тогда, взяв отношение
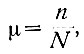 (3.1)
(3.1)получим параметр, называемый частостью (или частотой) появления события.
Важность указанного параметра характеризуется законом больших чисел. Этот закон, доказательство которого здесь опускается, говорит, что при достаточно большом числе измерений частость события может сколь угодно мало отличаться от его вероятности. Благодаря этому, вероятность события может быть определена как отношение количества появившихся событий (n) к числу достаточно большого числа измерений (N).
Так, например, при проведении 55 замеров оказалось, что величина тока 37 раз была в заданном диапазоне (от 1 до 1,2 а). Необходимо определить вероятность того, что случайно измеренное значение тока будет находиться в этом диапазоне.
В рассматриваемом примере N = 55, а n = 37. Поэтому вероятность случайного события равна
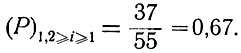
Как уже было показано ранее, вероятность события, которое обязательно произойдет, принято равным единице:
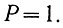
Так, например, при бросании шестигранного кубика сверху обязательно появится одна из шести цифр. Естественно, что вероятность события, о котором точно известно, что оно не произойдет, равна нулю. Поэтому можно записать, что вероятность случайного события всегда находится в пределах
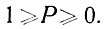 (3.2)
(3.2)Рассмотрим метод определения вероятностей сложных событий.
а) Вероятность несовместных событий
События А и В являются несовместными в том случае, если они не могут произойти одновременно. Так, например, при бросании кубика на его верхней грани одновременно не могут появиться две цифры.
Вероятность несовместных событий равна сумме вероятностей каждого из событий. Математически для двух событий это записывается следующим образом:
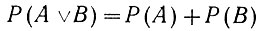 (3.3)
(3.3)("вероятность того, что появится событие А или В, равна сумме вероятностей событий А и В"). Доказательство этого уравнения вытекает из определения несовместных событий.
Поскольку логическое суждение "ИЛИ" выполняет логическое сложение, то условие (3.3) может быть записано также в ином виде:
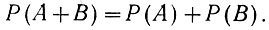 (3.3а)
(3.3а)Например, при бросании кубика появление "единицы" и "тройки" - несовместные события, ибо эти цифры одновременно появиться не могут. Поэтому вероятность того, что при бросании кубика появятся цифры "1" или "3", равна
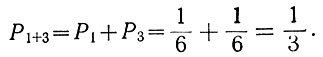
Вероятность события, которое обязательно произойдет, принята равной единице. Поэтому сумма вероятностей всевозможных несовместных событий, образующих случайную величину, также равна единице:
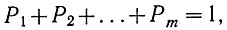 (3.4)
(3.4)
где P1 - вероятность первого события;
P2 - вероятность второго события;
. . . . . . . . . . . . . . . .
Рm - вероятность m-го события.
Поскольку несовместными называются события, которые не могут появиться одновременно, то вероятность одновременного (А и В) появления двух несовместных событий равна нулю:
или 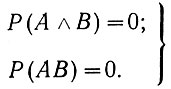 (3.5)
(3.5)
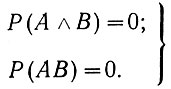 (3.5)
(3.5)б) Вероятности совместных событий
Совместными называются события, которые могут произойти (но не обязательно произойдут) одновременно.
Так, например, возьмем наугад одну из шахматных фигур. Будем при этом рассматривать два события: А - появление белой фигуры, В - появление ферзя. Поскольку в этом опыте может быть взят белый ферзь, то рассматриваемые события могут появиться одновременно, т. е. они являются совместными. Однако, если взят белый слон, то событие А произошло, а событие В - нет. Наконец, если взята черная ладья, то не произошло ни событие А, ни событие В.
Прежде чем рассмотреть методику определения вероятности совместных событий, необходимо отметить, что случайные события (совместные и несовместные) могут быть как зависимыми, так и независимыми.
Два события (А и В) называются независимыми, если появление одного из них (А) не изменяет вероятности появления другого. В противном случае события являются зависимыми.
Примеры независимых и зависимых событий.
1. Будем одновременно бросать два игральных кубика, на гранях каждого из которых написаны цифры от 1 до 6. Пусть при этом нас интересуют следующие события: одновременное появление на обоих кубиках грани с цифрой "четыре". Появление этой цифры на одном из кубиков не зависит от того, какая цифра появилась на другом кубике. Поэтому рассматриваемые события (появление цифры "четыре" на каждом из кубиков) являются независимыми.
2. В ящике лежат три шара, два из которых - черные, а один - белый. Рассмотрим следующие два события: появление по очереди двух шаров. Пусть при этом появление белого шара первым является событием А, а вторым - событием В. Вытащим теперь из ящика два шара. Легко увидеть, что если первый из двух взятых шаров белый, то второй обязательно будет черный, т. е. в этом случае вероятность события В равна нулю. Если первый шар оказался черным, то второй шар может быть и белым, и черным, т. е. вероятность события В уже не равна нулю. Следовательно, рассматриваемые события (А и В) являются зависимыми.
Вероятность зависимого события (В) называется условной, так как она определяется в зависимости от исхода другого события (А). Обозначается условная вероятность символом

Рассмотрим методику определения вероятности двух совместных событий.
Как следует из примера с шахматными фигурами, в этом случае при проведении N измерений могут произойти следующие три вида событий:
1) появление события А (nА раз);
2) появление события В (nВ раз);
3) появление обоих событий: А и В (l раз).
Поэтому в соответствии с законом больших чисел вероятность одновременного появления двух (А и В) событий определяется равенством
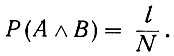
Вероятность же появления события А равна
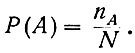
Условная вероятность события В является вероятностью появления этого события при условии появления события А. Как было показано выше, событие А происходит nА раз. Поскольку в этих nА случаях событие В появляется только l раз, то
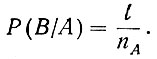
Следовательно, вероятность одновременного появления двух (А и В) зависимых совместных событий равна
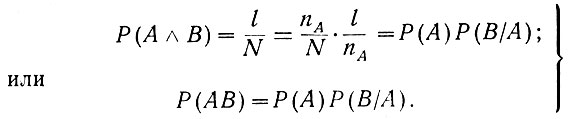 (3.6)
(3.6)Как следует из определения независимых событий, вероятность одновременного появления двух независимых совместных событий (ур. 3.6) равна
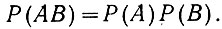 (3.6а)
(3.6а)Нетрудно заметить, что вероятность появления одного из совместных событий (А или В, но не А и В) равна
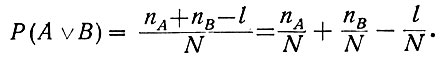
В этом уравнении вычитаются случаи (l), когда появляются одновременно события А и В, ибо рассматривается вероятность события А или В.
Поэтому вероятность появления одного из совместных событий определяется уравнением
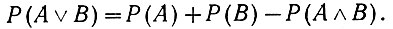
Подставив в это выражение значение вероятности Р(А ∧ В) (ур. 3.6), получаем для зависимых событий
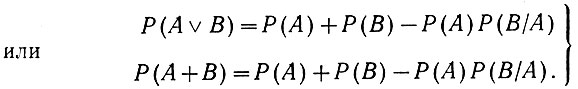 (3.7)
(3.7)Для независимых событий (ур. 3.6а) это выражение принимает следующий вид:
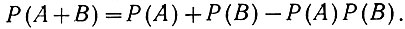 (3.7а)
(3.7а)Пример 1. При одновременном бросании двух одинаковых кубиков необходимо определить вероятность появления цифры "1" сразу на двух кубиках.
При бросании двух кубиков единица может появиться на одном или на двух кубиках сразу. Поэтому рассматриваемые события являются совместными. Поскольку же вероятность появления единицы на одном из кубиков не зависит от того, какая цифра появилась на другом кубике, то рассматриваемые события являются независимыми.
Вероятность появления единицы на первом кубике равна
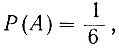
на втором кубике -
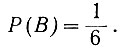
Поэтому (ур. 3.6а) вероятность появления единицы на обоих кубиках равна
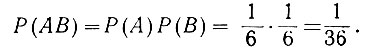
Пример 2. Определить вероятность появления цифры "3" только на одном из кубиков при бросании двух кубиков сразу.
В данном случае, как и в предыдущем, события являются совместными и независимыми.
Вероятности появления цифры "3" на первом и втором кубиках равны:
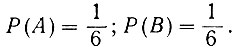
Тогда вероятность появления тройки на одном из кубиков (но не на двух сразу) равна (ур. 3.7а)
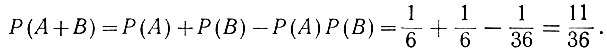

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
