
2. Характеристики случайных величин
Случайный процесс характеризуется случайной функцией, состоящей (рис. 3.1) из семейства многих реализаций.
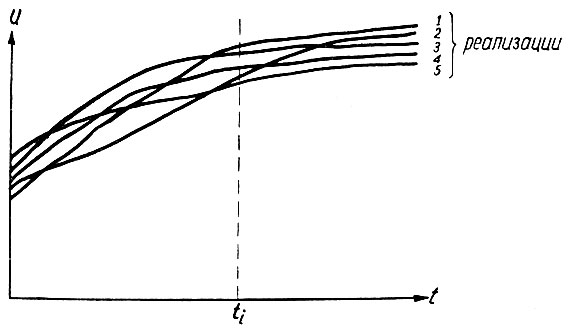
Рис. 3.1. Случайная функция времени
Рассмотрим, например, характер изменения напряжения на аккумуляторе заданного типа во время его заряда.
Предположим, что заряд аккумулятора ведется постоянным током при неизменной температуре помещения. Совершенно одинаковых аккумуляторов нет. Поэтому характеристики каждого аккумулятора зависят от состава и активной площади его электродов, состава и объема электролита, теплопередачи ящика аккумулятора и множества других причин, которые нельзя учесть достаточно точно. Следовательно, заряд аккумулятора является случайным процессом.
Если мы запишем напряжение аккумулятора во время заряда, то получим первую реализацию случайной функции (рис. 3.1). Повторение этого опыта на другом аккумуляторе того же типа дает вторую реализацию случайной функции. Так, повторяя опыты с другими аккумуляторами, можно получить случайную функцию, состоящую из отдельных реализаций.
Если нас интересуют характеристики заряда одного аккумулятора (а не аккумуляторов заданного типа), то случайная функция может быть получена в результате проведения серии зарядов одного и того же аккумулятора.
Если семейство реализаций случайной функции (рис. 3.1) рассечь вертикальной линией, то получим случайную величину для заданного (ti) момента времени. Эта величина, как было уже показано выше, состоит из отдельных случайных событий (на рис. 3.1 таких событий пять).
Для того чтобы определить неслучайную величину, достаточно найти характеризующее ее число. Так, например, фраза "неслучайное напряжение в данный момент времени (ti) равно пяти вольтам" полностью определяет неслучайную (детерминированную) величину (в данном случае - напряжение) в указанный момент времени.
Иначе обстоит дело со случайными величинами. Случайная величина считается заданной тогда, когда известен закон распределения вероятностей этой величины, т. е. определены вероятности всех ее значений (например, напряжений), имеющих место в исследуемой точке системы в заданный момент времени (ti).
Чтобы определить случайную функцию, кроме того, надо знать влияние одной случайной величины на другие. Эта взаимозависимость случайных величин, называемая корреляцией, будет рассмотрена в следующей главе.
Случайные процессы, изучаемые теорией вероятностей, могут быть как стационарными, так и нестационарными. Ниже нами рассматриваются только стационарные случайные процессы, вероятностные характеристики которых не изменяются во времени. Это связано с тем, что теория стационарных случайных процессов является наиболее простой и достаточно хорошо разработанной, а изучение нестационарных случайных процессов выходит за рамки данной книги.
Стационарные случайные процессы, как правило, обладают очень важным свойством, называемым эргодическим. Это свойство заключается в том, что каждая отдельная реализация случайной функции, определенная в течение достаточно длительного времени, с точки зрения теории вероятностей полностью определяет вое семейство реализаций случайной функции. В этом случае исследование семейства реализаций может быть заменено изучением только одной кривой - одной реализации случайной функции. Поэтому в стационарных процессах случайная величина получается уже не исследованием семейства реализаций случайной функции в заданный момент времени (рис. 3.1), а рассечением одной имеющейся реализации случайной функции вдоль ее оси времени.
Поскольку в стационарном процессе одна реализация определяет всю случайную функцию, то мы в дальнейшем будем ее просто называть случайной функцией, опуская слово "реализация".
Следует иметь в виду, что случайная функция не является "абсолютно" случайной, ибо в большинстве случаев нам все же известны некоторые ее основные черты, в какой-то степени характеризующие ее. Поэтому случайная функция обычно не является совсем произвольной и на нее могут быть наложены определенные ограничения.
Так, например, иногда можно установить участок частотного спектра, из которого состоит функция; часто можно задать предельные значения функции или границы изменения ее производной. Благодаря этому для каждой случайной функции имеется определенный закон распределения вероятностей ее случайных величин.
Случайные величины, из которых состоит случайная функция, могут изменяться либо дискретно (рис. 3.2), либо непрерывно (рис. 3.3).
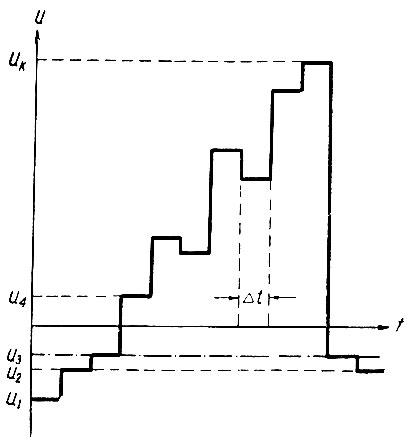
Рис. 3.2. Ступенчатая случайная функция
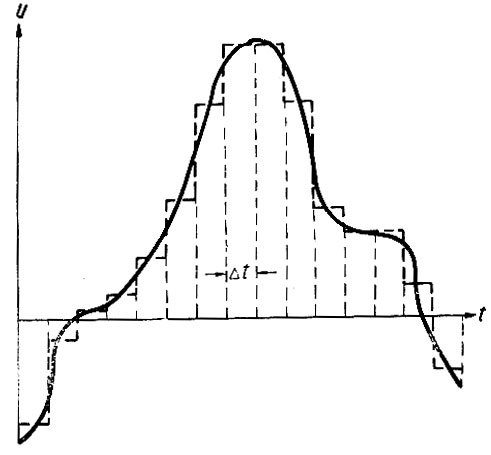
Рис. 3.3. Непрерывная случайная функция
Рассмотрим вначале, как определяются законы распределения вероятностей дискретной случайной величины.
Для этого подсчитаем для каждой ступеньки напряжения (рис. 3.2) количество ее повторений:
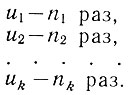
Далее определим общее количество (N) ступенек на рассматриваемом участке случайной функции. Это количество характеризует число проведенных опытов измерения случайной величины (напряжения).
Если полученные значения повторений (n1÷nk) каждой ступеньки разделить на общее число ступенек рассматриваемого участка функции, то определим ряд распределения дискретной случайной величины (табл. 3.1).
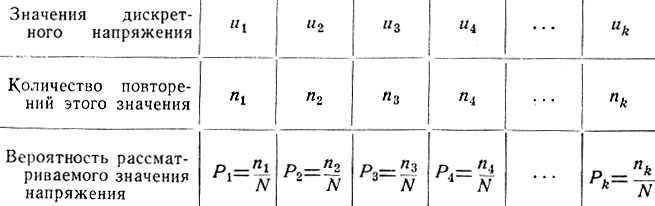
Таблица 3.1
Кроме того, дискретная случайная величина может быть определена функцией распределения.
Указанная функция может быть построена по полученным выше данным (u1, u2, uk и N). Для этого (рис. 3.4) по оси абсцисс отложим имеющиеся на случайной функции (рис. 3.2) дискретные значения напряжения, а по оси ординат - отношение числа ступеней, у которых напряжение меньше указанного на оси абсцисс, к общему числу опытов (N).
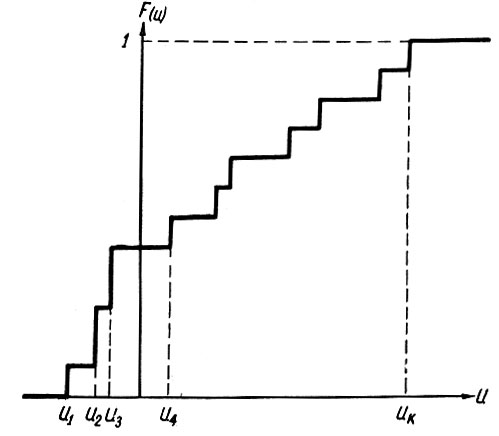
Рис. 3.4. Функция распределения вероятностей дискретной случайной величины
Так, например, при u2 ≥ u ≥ u1 по оси ординат откладываем величину n1/N, при u3 ≥ u ≥ u2 величина ординаты равна 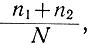 при
при 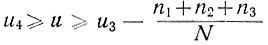 и т. д.
и т. д.
Построенная таким образом функция имеет вид ступенчатой кривой и называется функцией распределения вероятностей дискретной случайной величины.
Для того чтобы построить функцию распределения вероятностей непрерывной случайной величины можно непрерывную случайную функцию (рис. 3.3) заменить ступенчатой кривой с равномерным шагом Δt. Далее функция распределения строится как и в предыдущем случае, с той лишь разницей, что полученная ступенчатая функция распределения вероятностей заменяется, по возможности, совпадающей с ней непрерывной кривой (рис. 3.5).
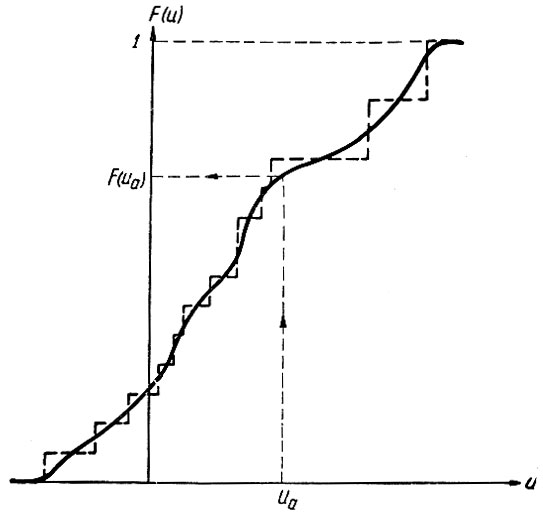
Рис. 3.5. Функция распределения вероятностей непрерывной случайной величины
Функция распределения вероятностей как дискретной, так и непрерывной случайной величины позволяет по заданному напряжению (uа, рис. 3.5) определить вероятность того, что любое напряжение, взятое на случайной функции, будет меньшим, чем заданное (uа).
В предельных случаях имеем следующее. Вероятность того, что любое напряжение меньше минус бесконечности, равна нулю, а вероятность того, что это напряжение меньше плюс бесконечности, - равна единице.
Другой кривой, характеризующей непрерывную случайную величину, является дифференциальная функция распределения вероятностей.
Эта характеристика, показанная на рис. 3.6, может быть получена путем дифференцирования функции распределения вероятностей:
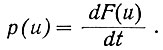 (3.8)
(3.8)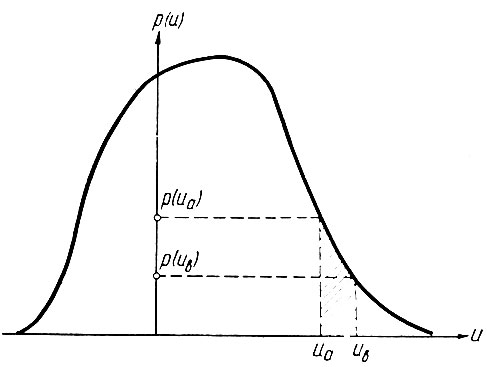
Рис. 3.6. Дифференциальная функция распределения вероятностей (функция распределения плотности вероятностей) непрерывной случайной величины
Однако дифференциальная функция распределения вероятностей может быть получена также и непосредственно по случайной функции времени.
Для определения дифференциальной функции распределения по непрерывной случайной функции времени ее необходимо, как это уже делалось при построении функции распределения, заменить ступенчатой кривой. Практически же, для того чтобы ускорить построение, оно выполняется следующим образом (рис. 3.7). Выбираем интервал времени и проводим (нижний график) через Δt линии, пересекающие случайную функцию в N точках. Затем с произвольно выбранным интервалом Δu проводим прямые, параллельные оси времени. Деля число точек, находящихся в каждом интервале Δu, на общее количество точек (N), получаем соответствующую ординату дифференциальной функции (пунктирные площадки на верхнем графике рис. 3.7). Если эту ступенчатую кривую заменить плавной, то получим дифференциальную функцию распределения непрерывной случайной величины.
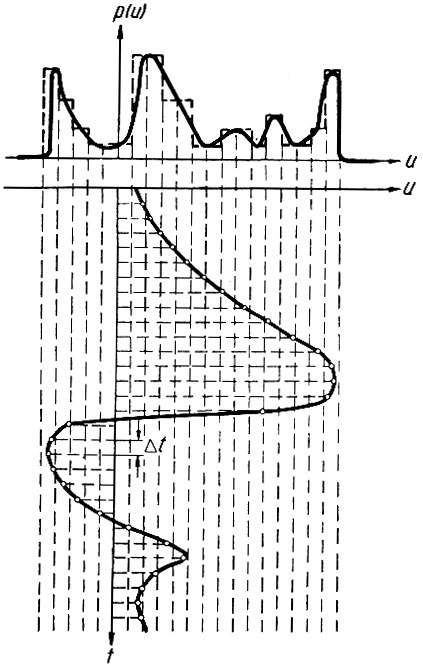
Рис. 3.7. Построение дифференциальной функции распределения вероятностей непрерывной случайной величины
Отметим одну характерную особенность, отличающую дифференциальную функцию распределения вероятностей непрерывной величины (рис. 3.6) от ряда распределения дискретной величины (табл. 3.1).
Соответствующее значение ряда распределения определяет вероятность того, что любое случайно измеренное напряжение будет равно заданному. Так, например (табл. 3.1), P1 определяет вероятность того, что случайно измеренное напряжение равно u1.
Предположим теперь, что ординаты ступенчатой кривой распределения, полученной на рис. 3.7 (пунктирная кривая на верхнем графике), также определяют вероятность того, что измеренное напряжение находится в заданном интервале Δu. Вероятность того, что измеренное напряжение находится в одном из k имеющихся интервалов Δu, равна единице:
 (3.9)
(3.9)где
Р1 - вероятность того, что измеренное напряжение находится на первом интервале Δu;
Р2 - то же на втором интервале Δu и т. д.
Если увеличивать число (k) интервалов Δu, то нетрудно заметить, что в пределе (k → ∞) каждый из указанных интервалов превратится в точку. В этом случае вероятность того, что любое случайно измеренное напряжение окажется в одном из интервалов, превращается в вероятность того, что измеренное напряжение равно заданному (интервал превращается в точку).
Вместе с тем сумма вероятностей попадания напряжения в заданные k точек остается неизменной и равной (ур. 3.9) единице. Поэтому (при k = ∞) вероятность того, что измеренное напряжение попало в заданную точку (равно заданной величине), оказывается равной нулю.
Вместе с тем любая ордината дифференциальной функции распределения, полученной на рис. 3.7 для непрерывной случайной величины, не равна нулю. Это происходит потому, что при переходе от дискретной случайной величины к непрерывной вместо вероятности (Р) по оси ординат откладывается плотность вероятности (р), равная частному от деления вероятности на величину рассматриваемого интервала напряжения:
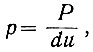
где du - ширина рассматриваемого интервала при k = ∞.
Поэтому дифференциальную функцию распределения вероятностей непрерывной случайной величины называют также функцией распределения плотности вероятностей.
Вероятность того, что случайно измеренное напряжение окажется в пределах от uа до ub (рис. 3.6), определяется по функции распределения плотности интегралом
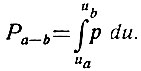 (3.10)
(3.10)Вероятность всевозможных событий равна единице (ур. 3.4). Поэтому
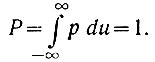 (3.11)
(3.11)Иначе говоря, площадь, ограниченная кривой p(u) = f(u) и осью абсцисс (u), всегда принимается равной единице. Поэтому вероятность того, что данное напряжение находится в пределах ub ≥ u ≥ uа, графически (рис. 3.6) определяется как отношение заштрихованной площади ко всей площади, ограниченной кривой p(u) = f(u) и осью абсцисс.
При рассмотрении случайных функций необходимо обратить внимание на существование двух различных понятий средних значений этих функций.
Прежде всего существует среднее по времени значение случайной величины. Для ступенчатой случайной функции (рис. 3.2) среднее по времени значение случайной величины определяется уравнением
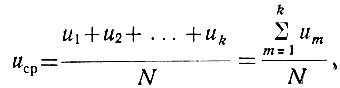
где u1÷uk - величины напряжения на соответствующих участках Δt;
N - общее число участков Δt, из которых состоит рассматриваемый период изменения случайной функции (T).
Умножив числитель и знаменатель этого уравнения на Δt, получаем
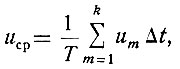 (3.12)
(3.12)где T = NΔt - рассматриваемый период изменения случайной функции.
Для непрерывной формы случайной функции (Δt → 0) уравнение (3.12) принимает следующий вид:
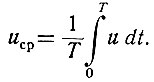
В случае же, когда необходимо определить среднее значение функции в бесконечно большом (от -∞ до +∞) интервале времени, это уравнение записывается в несколько ином виде:
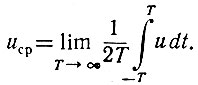 (3.13)
(3.13)Это среднее значение является той величиной, с которой всегда приходится иметь дело в любых величинах: случайных и неслучайных.
Кроме того, для случайных величин существует еще среднее по множеству значение, называемое также математическим ожиданием. Это среднее значение определяется для ступенчатой случайной функции уравнением
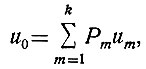 (3.14)
(3.14)где um - величина напряжения на m-ом участке Δt (рис. 3.2);
Рm - вероятность этого напряжения.
Вероятность может быть выражена через плотность вероятности
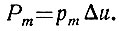
Поэтому уравнение (3.14) можно записать в несколько ином виде:
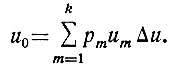
Следовательно, для непрерывной случайной функции (Δu → 0) можно записать
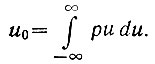 (3.15)
(3.15)Как известно из математики, абсцисса центра тяжести плоской однородной фигуры, образованной (рис. 3.6) функцией p = f(u) и осью абсцисс (u), определяется зависимостью
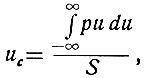
где S - площадь этой фигуры.
Согласно уравнению (3.11) площадь (S), ограниченная функцией распределения плотности вероятностей и осью абсцисс, всегда равна единице. Поэтому уравнение (3.15) определяет абсциссу центра тяжести этой фигуры.
Как уже отмечалось ранее, при определенных ограничениям любые стационарные случайные процессы обладают так называемым эргодическим свойством. Согласно этому свойству, доказательство которого здесь опускается, для эргодических процессов среднее по множеству значение случайной величины всегда равно среднему по времени значению этой величины. Поэтому можно записать, что
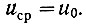 (3.16)
(3.16)Отклонением случайной величины называется разница
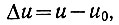 (3.17)
(3.17)где u - текущее значение случайной величины;
u0 - ее среднее значение (математическое ожидание).
Часто в теории вероятностей пользуются величиной, называемой дисперсией случайной величины. Дисперсия характеризует рассеивание случайной величины возле ее среднего значения и определяется как среднеквадратичное отклонение случайной величины от ее среднего значения:
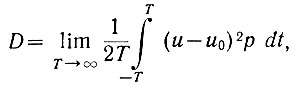 (3.18)
(3.18)где р - функция распределения плотности вероятностей.
Если дисперсия равна нулю, то это значит, что случайная величина превратилась в постоянное напряжение, равное u0.
Для того чтобы получить параметр, имеющий размерность случайной величины (u) и ее математического ожидания (u0), вместо дисперсии часто употребляют параметр, называемый среднеквадратичным (или стандартным) отклонением случайной величины:
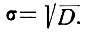 (3.19)
(3.19)Ранее было показано, что функция плотности распределения вероятностей может быть определена на основе экспериментальных данных. Однако довольно большое число случайных величин имеют так называемую нормальную функцию распределения плотности вероятностей. Эта функция определяется по закону Гаусса:
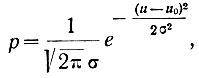 (3.20)
(3.20)где σ - среднеквадратичное отклонение;
u0 - среднее значение случайной величины (математическое ожидание).
Нормальная функция распределения плотности вероятностей имеет вид кривой, показанной на рис. 3.8.
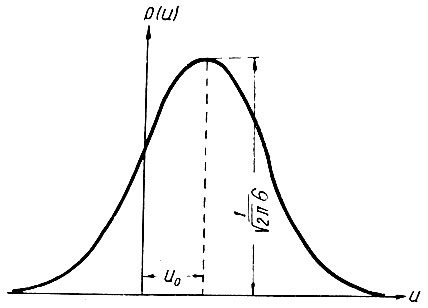
Рис. 3.8. Нормальная кривая распределения вероятностей
Следует отметить, что нормальная функция (ур. 3.20) всегда симметрична относительно вертикальной оси, проходящей через точку ее максимума. Поэтому математическое ожидание (u0), характеризующее абсциссу центра тяжести фигуры (рис. 3.8), образованной нормальной функцией и осью абсцисс, в данном случае определяет напряжение, при котором нормальная функция имеет максимум, равный
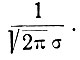
Если случайная функция времени не имеет постоянной составляющей, то математическое ожидание (ур. 3.16) равно нулю. В этом случае (рис. 3.9) нормальная кривая становится симметричной относительно оси ординат.
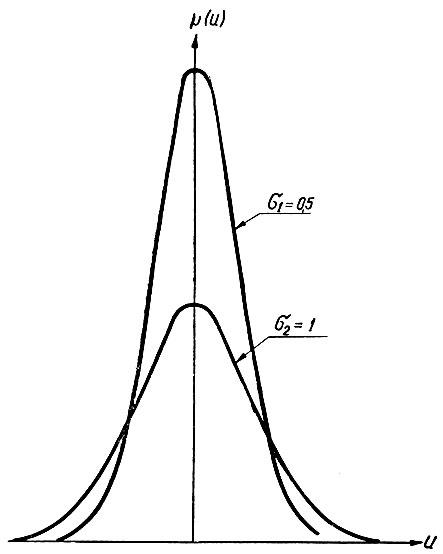
Рис. 3.9. Нормальная кривая распределения вероятностей случайной величины, не имеющей постоянной составляющей
Как следует из уравнения (3.20), среднеквадратичное отклонение (σ) является мерой быстроты спадания нормальной функции. Влияние величины σ на характер этой функции показано на 4 рис. 3.9.

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
