
3. Энтропия случайного события
Электрический ток используется для двух целей. Во-первых, электрический ток является носителем энергии, применяемой в различных системах и устройствах. Во-вторых, при помощи электрического тока осуществляется передача информации - сведений или сообщений о каком-либо явлении или процессе.
При передаче энергии электрическим током нас в первую очередь интересует коэффициент полезного действия передачи. Это объясняется тем, что энергию необходимо передавать с наименьшими потерями.
Существенной же особенностью любой передаваемой информации является ее независимость от количества энергии, затраченной на передачу электрического тока, несущего эту информацию. Иначе говоря, одна и та же информация может быть передана при помощи электрического тока различной величины.
Поэтому в случае, когда электрический ток используется для передачи информации, вопросы, связанные с получением максимального значения коэффициента полезного действия, отходят на задний план. Главным является передача максимального количества информации в заданный промежуток времени.
Рассматривая любую физическую систему (в том числе и систему автоматического управления), можно сказать, что кое-что мы о ней знаем, но некоторые ее параметры и характеристики нам неизвестны. В таком случае говорят, что система не полностью определена. Мерой этой неопределенности служит энтропия (Н).
Проделаем следующий опыт. Пусть имеется система, энтропия (неопределенность) которой равна Hнач. После получения нами информации об этой системе ее неопределенность уменьшается и характеризуется энтропией Hкон.
Количество полученной при этом информации (q) определяется равенством
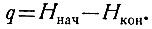 (3.21)
(3.21)Таким образом, количество информации равно энтропии, устраненной благодаря полученному сообщению. В случае, когда полученное сообщение полностью снимает неопределенность рассматриваемой физической системы (Hкон = 0), количество информации численно равно энтропии системы:
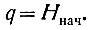 (3.21а)
(3.21а)а) Методика определения энтропии дискретного сигнала
В самом простом случае энтропия (неопределенность) характеризуется возможностью одного из двух сообщений: "событие имеет место" или "событие отсутствует". Более кратко это записывается в виде
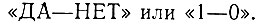
Поэтому за единицу энтропии принимается неопределенность выбора одного из двух возможных исходов: "ДА-НЕТ" или "1-0" (двоичная единица). Поскольку же количество информации (ур. 3.21) должно измеряться в тех же единицах, то этот сигнал определяет также и единицу количества информации.
Определим далее энтропию простого события при наличии неопределенности выбора одного из m возможных исходов.
Для этого рассмотрим следующий пример. Необходимо определить энтропию (неопределенность) включения одной из восьми ячеек (рис. 3.10).
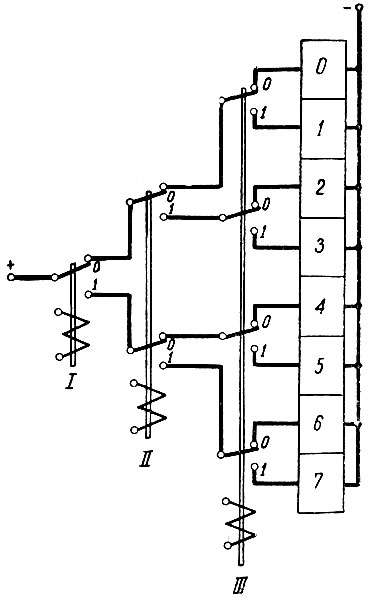
Рис. 3.10. Схема выбора одной из восьми ячеек
Как следует из рисунка 3.10, для того чтобы сказать, какая из восьми ячеек включена, необходимо знать положение трех контакторов (0 - верхнее положение контактора, 1 - нижнее положение).
Эти данные могут быть сведены в таблицу (см. табл. 3.2).
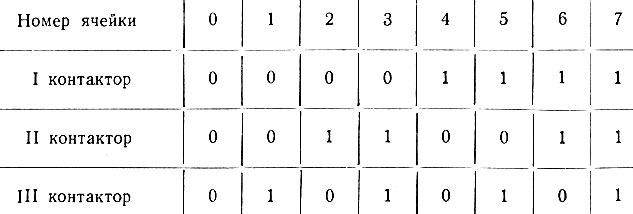
Таблица 3.2
Следовательно, энтропия выбора одной из восьми ячеек равна трем (неопределенность положения трех контакторов). Математически это записывается следующим образом:
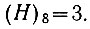
Это равенство может быть записано в несколько ином виде:
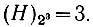
Следовательно, энтропия равна не количеству ячеек (здесь - 8), а степени, в которую надо возвести цифру "2", чтобы получить рассматриваемое количество ячеек (H = 3 и 23 = 8).
Поэтому в общем виде энтропия события (неопределенность появления одного из m возможных значений) равна:
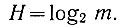 (3.22)
(3.22)Это уравнение, определяющее энтропию простого события, называется законом Хартли.
В рассмотренном выше примере m = 8; поэтому энтропия выбора одной ячейки из 8 равна
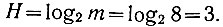
Следует иметь в виду, что для простоты проведения математических операций уравнение (3.22) считают справедливым и для тех случаев, когда m - не целое число.
Теория информации очень тесно связана с теорией вероятностей. Действительно, пусть все m рассмотренных выше значений случайной величины имеют одну и ту же вероятность. Тогда вероятность появления одного из них равна
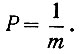
В этом случае (ур. 3.22) энтропия случайного события, заключающегося в появлении одного из m значений, записывается в следующем виде:
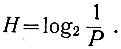 (3.23)
(3.23)Таким образом, чем больше вероятность события, тем меньше его энтропия (неопределенность). Действительно, если нам точно (с вероятностью Р = 1) известно, что будет включена ячейка № 7 (рис. 3.10), то энтропия рассматриваемого события (неопределенность того, будет включена ячейка № 7 или нет) равна нулю.
Уравнение (3.23) может быть записано в несколько ином виде:
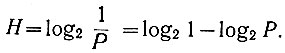
Но log2 1 = 0.
Поэтому можно записать, что
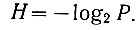 (3.24)
(3.24)Это уравнение определяет энтропию одного (простого) события. Естественно, что сложное событие, состоящее из n равновероятностных простых независимых событий, имеет (ур. 3.6а) в n раз большую энтропию:
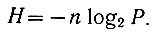 (3.25)
(3.25)При этом следует иметь в виду (ур. 3.2), что вероятность всегда находится в пределах 1 ≥ Р ≥ 0. Поэтому log2 Р меньше нуля, т. е. энтропия всегда положительна.
Рассмотрим случай, когда различные события имеют разную вероятность. Тогда по аналогии с уравнением (3.24) для каждого события можно записать:
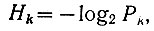 (3.26)
(3.26)где k - номер события (k = 1, 2, ..., m).
Уравнение (3.26) определяет энтропию одного события с вероятностью его появления Рk.
Предположим далее, что имеется m различных событий с вероятностями их появления:
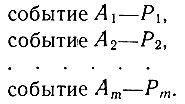
В общем случае сразу может произойти несколько событий. Поэтому рассматриваемые события являются совместными. Кроме того, пусть эти события - независимые.
Следовательно, если событие А1 имеет вероятность Р1, то (ур. 3.6а) вероятность того, что одновременно появится два события А1, равна
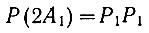
или
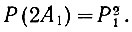
Естественно, что вероятность появления a раз события А1 равна
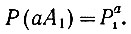 (3.27)
(3.27)Рассмотрим далее сложное событие - одновременное появление n простых событий А1, A2, ..., Аm. Поскольку вероятность появления сигнала А1 равна Р1, то в сложном событии будет P1 событий А1.
Вероятность того, что событие А1 встретится в сложном событии (в n простых событиях) nР1 раз, равна (ур. 3.27)
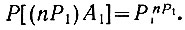
Аналогично этому можно сказать, что вероятность появления nР2 раз события А2 равна
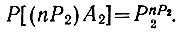
Поэтому (ур. 3.6а) вероятность сложного события, состоящего из событий типа А1, А2, ..., Аm, равна
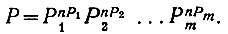
Следовательно, (ур. 3.24) энтропия рассматриваемого сложного события определяется следующей зависимостью:
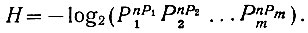
Преобразуя логарифмические выражения, содержащиеся в этом уравнении, получаем
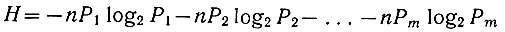
или
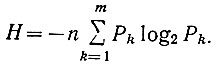 (3.28)
(3.28)Уравнение (3.28), определяющее энтропию сложного события, которая заключается в одновременном появлении n простых событий m типов, имеющих различную вероятность, называется уравнением Шеннона.
Если вероятности всех m типов событий равны (Р1 = Р2 = ... = Рm = Р), то уравнение Шеннона приобретает вид
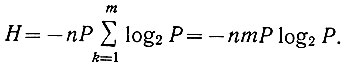
Поскольку же вероятность m равновероятностных событий равна Р = 1/m, то предыдущее уравнение может быть записано в следующем виде:
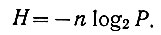
Таким образом (что и следовало ожидать), уравнение (3.25) является частным случаем уравнения Шеннона.
В случае, когда рассматривается простое событие (n = 1), уравнение (3.28) записывается в следующем виде:
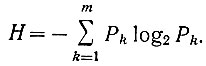 (3.28а)
(3.28а)Необходимо обратить внимание на одно существенное различие уравнений (3.24) и (3.28а). Уравнение (3.24) дает энтропию одного из m равновероятностных событий. Уравнение же (3.28а) определяет среднюю энтропию, приходящуюся на одно из m событий, имеющих различную вероятность.
Следует отметить, что, согласно второму закону термодинамики (закону Больцмана), энтропия замкнутого пространства определяется уравнением
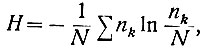 (3.29)
(3.29)где N - общее число молекул в данном пространстве;
n1 - число молекул, имеющих скорость V1 + ΔV;
n2 - число молекул, имеющих скорость V2 + ΔV и т. д.;
ΔV - приращение скорости.
Ранее (ур. 1.4) было показано, что
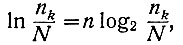
где n - коэффициент пропорциональности.
Отношение 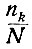 есть не что иное, как вероятность того, что молекулы имеют скорость Vk + ΔV. Поэтому можно записать, что
есть не что иное, как вероятность того, что молекулы имеют скорость Vk + ΔV. Поэтому можно записать, что
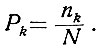
Следовательно (ур. 3.29), энтропия определяется выражением
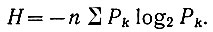 (3.30)
(3.30)Сравнивая это уравнение с законом Шеннона (ур. 3.28), становится понятным, почему Шеннон назвал степень неопределенности физической системы энтропией.
Ранее понятие энтропии использовалось только в термодинамике, где энтропия характеризовала необратимое рассеяние энергии замкнутой физической системой и могла только возрастать.
Однако в кибернетике энтропия может не только увеличиваться, но и уменьшаться, так как здесь понятие энтропии тесно связано с мерой неопределенности. Поэтому увеличение количества информации (меры порядка) приводит к уменьшению неопределенности, т. е. энтропии.
Между тем нет никакого противоречия в том, что в кибернетике энтропия как увеличивается, так и уменьшается, а в замкнутой физической системе энтропия может только возрастать. Это происходит потому, что термодинамика рассматривает энтропию ограниченной системы, в то время как Вселенная необъятна, и в ней, очевидно, существуют области, где могут создаваться новые "солнечные" системы и, следовательно, энтропия (в термодинамическом смысле) может также уменьшаться.
Рассмотрим пример определения энтропии.
В Риге по ул. Ленина проходят четвертый, шестой и седьмой маршруты троллейбусов. Троллейбусы идут с интервалами: № 4 - 3 мин., № 6 - 4 мин. и № 7 - 5 мин. Необходимо определить среднюю энтропию сообщений о всех трех маршрутах троллейбусов.
Вероятность того, что подъезжает троллейбус любого номера, равна единице. Поэтому
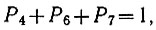 (3.31)
(3.31)где Р4, Р6, P7 - соответственно вероятности появления троллейбусов № 4, № 6 и № 7.
Кроме того, исходя из заданных интервалов движения троллейбусов следует, что
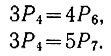
Подставив значения Р6 и Р7 в уравнение (3.31), определяем вероятность появления троллейбуса № 4:
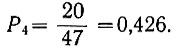
Затем из уравнения (3.31) могут быть определены также вероятности появления троллейбусов № 6 и № 7:
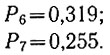
Зная вероятность каждого события, можно определить (ур. 3.28а) среднюю энтропию рассматриваемых событий:
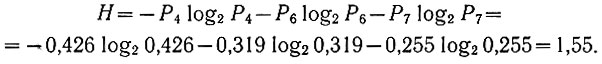
В двоичной системе счисления приходится оперировать с двумя случайными событиями (появление нуля и единицы). Поэтому рассмотрим далее сложное случайное событие, состоящее из двух (m = 2) простых случайных событий.
Средняя энтропия, приходящаяся на каждое из этих простых событий (ур. 3.28а), определяется зависимостью
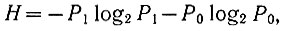 (3.32)
(3.32)где P1 и Р0 - вероятности появления единицы и нуля.
Обозначим вероятность появления единицы через
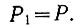
Поскольку вероятность всех (в данном случае - двух) событий должна быть равна единице:
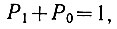
то вероятность второго события определится равенством
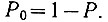
Подставив значения вероятностей Р1 и Р0 в уравнение (3.32), определим среднюю энтропию, приходящуюся на каждое простое событие (появление нуля или единицы):
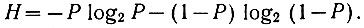 (3.33)
(3.33)Эта зависимость показана на рис. 3.11. Определяя максимум функции (3.33), нетрудно заметить, что средняя энтропия имеет максимум в том случае, когда вероятности обоих событий равны:
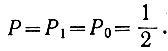 (3.34)
(3.34)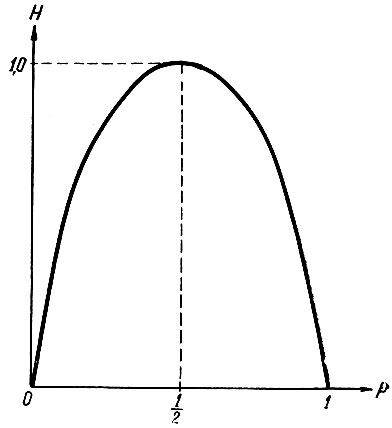
Рис. 3.11. Зависимость средней энтропии от вероятности появления одного из событий
При передаче информации, закодированной в двоичной системе счисления, количество информации, передаваемое одним сигналом, будет наибольшим в случае (ур. 3.21а), когда его энтропия имеет максимум. Поэтому необходимо стремиться к тому, чтобы в передаваемом сообщении вероятности появления нуля и единицы были по возможности одинаковыми.
До сих пор нами рассматривались только независимые события. Что касается зависимых событий, то здесь нужно обратить внимание на следующее.
Зависимость вероятности события В от исхода события A уже сама по себе дает некоторую информацию о событии В, тем самым уменьшая энтропию этого события. Поэтому энтропия зависимых событий (Hу) всегда меньше, чем энтропия (H) независимых событий:
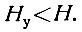 (3.35)
(3.35)Об этом принято говорить, что корреляция (зависимость) между событиями уменьшает энтропию (неопределенность).
б) Измерение энтропии непрерывного сигнала
Ранее (раздел 1-5) было показано, что непрерывная функция времени может быть с любой заданной точностью представлена конечным числом ее значений. Иначе говоря, всегда можно исходя из допустимой ошибки определить минимальную величину приращения функции (Δu) и заменить непрерывную функцию ступенчатой.
Практически это приращение определяется уравнением
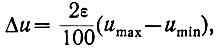 (3.36)
(3.36)где ε - допустимая ошибка в процентах; эта ошибка умножается на 2, ибо заданная ошибка определяет допустимые отклонения в обе стороны от истинного значения;
umax - максимальное значение непрерывной функции в рассматриваемом диапазоне;
umin - минимальное значение функции в этом диапазоне.
Используя это приращение, непрерывную кривую u = f(t) можно разделить на m дискретных значений, т. е. заменить рассматриваемую кривую ступенчатой функцией (рис. 3.12) со следующим количеством дискретных напряжений:
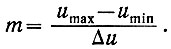 (3.37)
(3.37)Если решить совместно уравнения (3.36) и (3.37), то можно записать, что
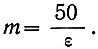 (3.38)
(3.38)Таким образом, исследование непрерывной случайной величины сводится к рассмотрению дискретной, принимающей m значений.
В случае, когда вероятности всех m событий равны, легко можно определить вероятность каждого из них (ур. 3.38):
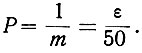 (3.39)
(3.39)Поэтому энтропия события (энтропия появления каждой ступеньки напряжения) определяется уравнением (3.24)
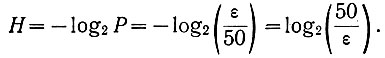 (3.40)
(3.40)Если рассматриваемые случайные события (появление ступенек) имеют различную вероятность, то их энтропия определяется уравнением Шеннона (ур. 3.28а).
В этом случае приращение функции (Δu) по-прежнему подсчитывается по уравнению (3.36) и принимается постоянным для всего рассматриваемого диапазона напряжения. Однако производная непрерывного напряжения в этом диапазоне изменяется. Поэтому ширина (Δtk) каждой ступеньки кривой напряжения (рис. 3.12) получается также переменной.
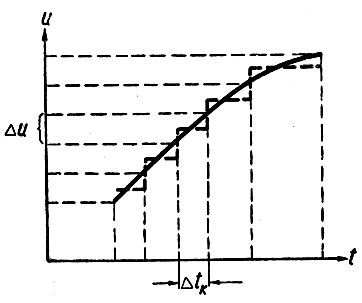
Рис. 3.12. Замена непрерывной кривой ступенчатой функцией
Подсчитаем минимальное значение интервала времени (Δtmin), соответствующего наиболее короткой во времени ступеньке. Это значение определяется из выражения
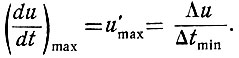
Следовательно,
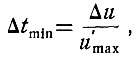 (3.41)
(3.41)где Δu - приращение, определяемое уравнением (3.36);
u'max - максимальное значение скорости изменения напряжения непрерывной кривой на рассматриваемом участке времени.
Подставив в уравнение (3.41) значение Δu (ур. 3.36), получаем
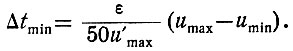 (3.42)
(3.42)Поделим энтропию события (появление ступеньки) на длительность (во времени) этой ступеньки. Полученное частное определит частоту, с которой должна регистрироваться информация, доставляемая этой ступенькой:
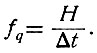 (3.43)
(3.43)Для минимального интервала времени это уравнение принимает следующий вид:
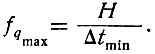 (3.44)
(3.44)Подставив в это уравнение значения H (ур. 3.40) и Δtmin (ур. 3.42), получаем
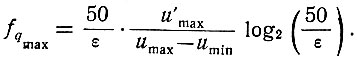 (3.45)
(3.45)Зависимость (3.45) характеризует максимальную частоту, с которой приемное устройство должно принимать информацию, даваемую непрерывным сигналом.
Пример. Определить максимальную частоту, с которой необходимо принимать информацию, даваемую синусоидальной кривой (f = 50 гц) при изменении ее от нуля до максимального (umax = 10 в) значения (рис. 3.13); допустимая ошибка ε = 5%.
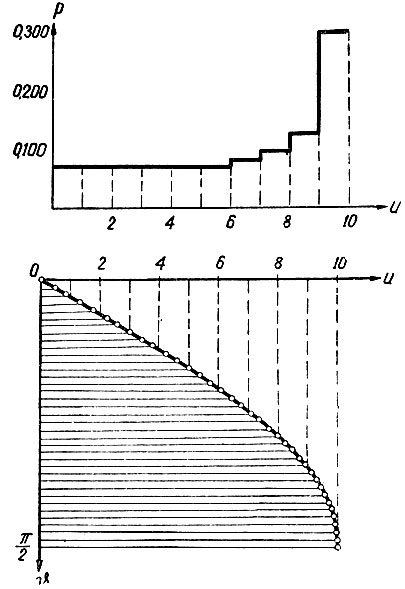
Рис. 3.13. Определение вероятностей диапазонов синусоидального напряжения
Прежде всего определим величину ступеньки кривой, аппроксимирующей синусоидальную функцию. Как следует из уравнения (3.36), эта ступенька равна
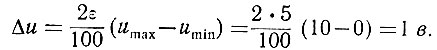
Количество ступенек (ур. 3.38) равно
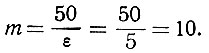
Таким образом, синусоидальная кривая заменяется ступенчатой функцией с десятью ступеньками.
Далее определим вероятность появления каждого из десяти рассматриваемых событий (каждой из десяти ступенек напряжения). Синусоидальная функция является периодической кривой, у которой вероятности одних и тех же участков напряжения (без учета его знака) повторяются через каждые четверть периода. Поэтому для определения этих вероятностей достаточно ограничиться рассмотрением синусоидальной функции при 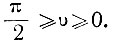
Выберем (рис. 3.13) шаг (Δυ) по оси абсцисс равным 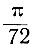 . Тогда на синусоидальной функции получим 37 точек (считая и начало координат). Подсчитаем теперь количество точек в каждом из десяти (m = 10) диапазонов напряжения (точку, оказавшуюся на границе диапазонов, будем считать в каждом диапазоне за половину) и поделим это количество на общее число точек (37). Этим определится вероятность каждой из десяти ступенек напряжения (случайных событий). Полученные данные сведем в таблицу (см. табл. 3.3).
. Тогда на синусоидальной функции получим 37 точек (считая и начало координат). Подсчитаем теперь количество точек в каждом из десяти (m = 10) диапазонов напряжения (точку, оказавшуюся на границе диапазонов, будем считать в каждом диапазоне за половину) и поделим это количество на общее число точек (37). Этим определится вероятность каждой из десяти ступенек напряжения (случайных событий). Полученные данные сведем в таблицу (см. табл. 3.3).

Таблица 3.3
В соответствии с приведенными данными строится ступенчатая кривая, показанная на верхнем графике рис. 3.13.
Поскольку вероятности отдельных ступенек напряжения оказались различными, то средняя энтропия одного из десяти (m = 10) событий определяется уравнением Шеннона (ур. 3.28а):
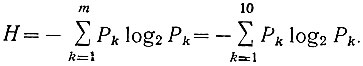
Подставляя в это уравнение значения вероятностей из таблицы 3.3, получаем
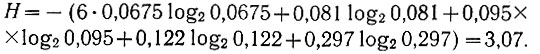
Если же принять вероятности всех ступенек одинаковыми (практически это значит, что синусоидальная функция на участке 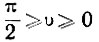 заменяется прямой линией), то энтропия каждого из событий определится уравнением (3.40):
заменяется прямой линией), то энтропия каждого из событий определится уравнением (3.40):
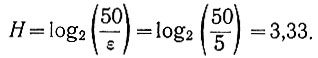
Естественно, что в этом случае упрощается вычисление, но уменьшается точность расчета.
Для определения максимальной частоты информации (ур. 3.45) необходимо знать максимальную скорость изменения напряжения. Эта скорость определяется очень просто.
Синусоидальная функция имеет вид
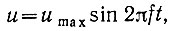
поэтому
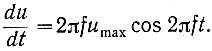
Приведенная зависимость имеет максимум при 2πft = 0, так как cos 0 = 1. Следовательно,
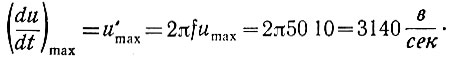
Поэтому максимальная частота, на которую должно быть рассчитано приемное устройство, равна (ур. 3.45)
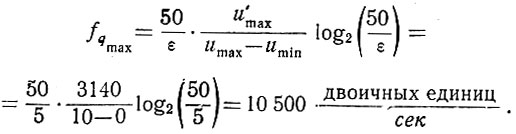

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
