4. Оптимальный код

Рассмотрим, каким образом необходимо кодировать информацию, передаваемую двоичным дискретным сигналом (1-0).

Ранее (раздел 3-3а) было показано, что для получения максимума энтропии двоичного сигнала необходимо выполнение двух условий:

а) вероятности появления единицы и нуля должны быть одинаковы и равны:

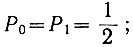
б) все сигналы должны быть независимы друг от друга.

Примем, что двоичная информация передается следующим образом: 1 - постоянное напряжение длительностью τ, а 0 - отсутствие напряжения в течение τ. Тогда по линии, или, как иногда говорят, по каналу, в одну секунду будет передаваться следующее количество сигналов (импульсов):

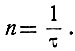
Следовательно, пропускная способность канала (максимальное количество сигналов, которое может быть передано по каналу в течение одной секунды) равна

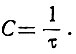(3.46)

Назовем оптимальным такой код, при котором по каналу будет передаваться максимальное количество информации. Шенноном доказано, что каким бы оптимальным ни был код, передавать сообщение по каналу можно со средней скоростью, не превышающей величины

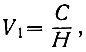(3.47)

где С - пропускная способность канала;

H - энтропия передаваемого сообщения.

Это уравнение называется первой теоремой Шеннона.

Рассмотрим пример определения максимально возможной скорости (V₁).

Латышский алфавит состоит из 30 букв (m = 30), включая "нулевую букву" - пропуск между словами. Примем для простоты, что вероятность появления всех букв одинакова. Тогда энтропия одной буквы (ур. 3.24) будет равна

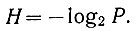
Так как вероятность появления всех букв принята одинаковой, то она равна

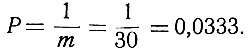
Поэтому энтропия одной буквы

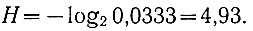
Примем, что пропускная способность канала С = 1000 импульсов (двоичных знаков) в секунду. Тогда текст сообщения при любом методе двоичного кодирования букв не может быть передан по каналу со скоростью большей, чем (ур. 3.47)

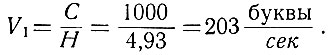
Для получения оптимального кода необходимо учесть статистические данные о передаваемом сообщении. При передаче наиболее часто встречающихся сигналов нужно делать код покороче, а для редко попадающихся сигналов код может быть и длинным.

Практически оптимальный код, называемый кодом Шеннона-Фено, создается следующим образом.

Все имеющиеся сигналы, которые необходимо закодировать, делятся на две группы так, чтобы вероятность появления каждой из этих групп сигналов была по возможности ближе к 1/₂. Это обеспечивает получение максимума информации (наибольшую энтропию сообщения). Далее одной из полученных групп присваивается символ "единица", а другой - "нуль". После этого сигналы, принадлежащие к каждой из групп, вновь делятся на две группы с вероятностью, по возможности близкой к 1/₂. Каждая из полученных групп вновь кодируется единицей и нулем, но уже расположенными в другом разряде. Процесс такого деления продолжается до тех пор, пока в каждой из групп останется по одному сигналу.

Рассмотрим методику построения кода Шеннона-Фено на следующем примере.

Имеется 10 сигналов с вероятностями их появления, показанными в таблице 3.4.

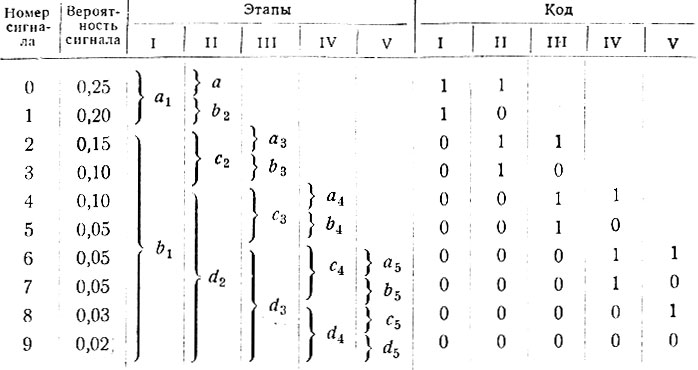
Таблица 3.4

Составление кода, как это видно из таблицы 3.4, распадается на пять этапов. На первом этапе сигналы делятся на две группы с примерно одинаковой вероятностью. В первую группу (a₁) входят сигналы № 0 и 1, в сумме имеющие вероятность 0,45, а во вторую - (b₁) - сигналы № 2÷9, вероятность появления которых равна 0,55. Сигналам первой группы присваивается единица, а сигналам второй группы - нуль.

Таким образом, появление в высшем разряде двоичного числа единицы будет говорить о том, что необходимо взять первую группу сигналов, а появление нуля - вторую группу.

На втором этапе первая группа сигналов (а₁) делится на две части и сигналу № 0 присваивается единица (в следующем после высшего разряде), а сигналу № 1 - нуль. Вторая группа сигналов (b₁) также делится на две части с примерно равной вероятностью. Первой части (с₂) дается единица, а второй (d₂) - нуль. Так продолжается до тех пор, пока не закончится полностью деление сигналов на группы, в каждой из которых в конце концов останется по одному сигналу.

Следует отметить, что десять сигналов могут быть закодированы (ур. 1.3) четырехразрядным числом. Однако в оптимальном коде различные сигналы имеют от двух до пяти разрядов. Естественно, что чем выше вероятность сигнала, тем короче его код.

Поэтому оптимальный код Шеннона-Фено строится таким образом, чтобы имеющиеся в нем сигналы (нуль и единица) имели по возможности равную вероятность появления.

Следует иметь в виду, что до сих пор нами рассматривался канал, в котором отсутствуют помехи, или канал без помех.

Рассмотрим влияние помех на примере, который был показан выше: информация передается десятью различными сигналами № 0÷9.

В случае, когда помехи в канале отсутствуют, при появлении сигнала мы, зная его код, с вероятностью, равной единице, можем сказать, что это сигнал, например, № 3 (рис. 3.14, а).

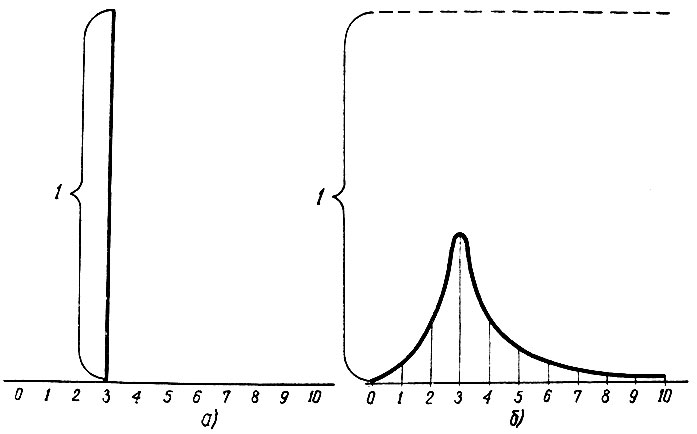
Рис. 3.14. Вероятность после прихода сообщения

Если же сигнал приходит с помехами, то мы не можем с вероятностью, равной единице, сказать, что это какой-то определенный, например № 3 (рис. 3.14, б), сигнал. В этом случае мы говорим, что наиболее вероятно, что это сигнал № 3, но и не исключена вероятность, что это другой сигнал. Характеристика распределения вероятности сообщения о сигнале показана на рис. 3.14, б.

Таким образом, при наличии помех происходит некоторая потеря информации. Эта потеря определяется равенством

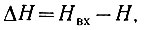(3.48)

где H_вх - количество информации, содержащейся в сигнале на входе канала;

H - то же на выходе канала.

Величина ΔН характеризует среднюю меру неопределенности, остающуюся после прихода сигнала.

При отсутствии помех максимальная скорость прохождения сообщения по каналу определялась уравнением (3.47). При наличии помех эта скорость из-за потерь информации (ур. 3.48) уменьшается и определяется уравнением

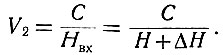(3.49)

Эта зависимость называется второй теоремой Шеннона. В реальных устройствах скорость V₂ и тем более скорость V₁ (ур. 3.47) еще не достигнуты, и пути их достижения пока неизвестны.