4. Системы с непосредственным измерением производной

В двух предыдущих случаях уравнения, описывающие экстремальный процесс управления, были заданы. Рассмотрим теперь случаи, когда эти уравнения неизвестны.

Предположим, что имеется дизель-генератор, работающий параллельно с энергосистемой. Необходимо обеспечить такое управление этим агрегатом, чтобы его коэффициент полезного действия был все время равен максимуму.

Ранее рассмотренные типы экстремальных систем автоматического управления здесь не могут быть применены, так как во-первых, уравнения, описывающие рабочие режимы дизель-генератора, неизвестны, и, во-вторых, из-за изменения температуры дизеля и параметров электрической системы нельзя подобрать неизменный режим работы агрегата, который был бы оптимальным в течение всего времени его работы.

Коэффициент полезного действия дизель-генератора при изменении количества подаваемого к дизелю топлива (q) изменяется в соответствии с кривой, показанной на рис. 6.7 сплошной линией. Математическое описание этой кривой неизвестно. Более того, эта кривая с течением времени (t) по неизвестному нам закону искажается и смещается (прерывистые кривые).

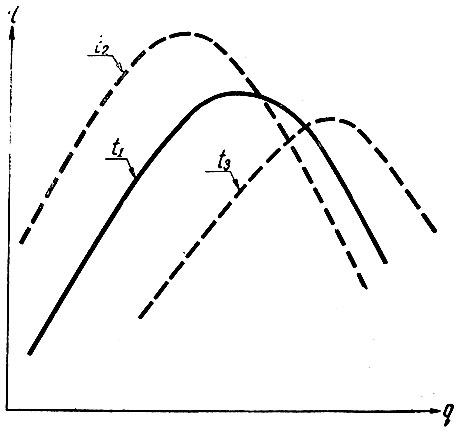
Рис. 6.7. Характеристика дизель-генератора

Какой бы ни была функция η = f(q), экстремальное значение коэффициента полезного действия дизель-генератора определяется зависимостью

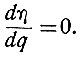
Поэтому для обеспечения экстремального управления дизель-генератором необходимо подсчитать коэффициент полезного действия, определить его производную по количеству топлива и так осуществлять управление, чтобы эта производная все время была равна нулю.

Схема системы, обеспечивающей такое управление, показана на рис. 6.8. На вход системы подаются параметры, характеризующие выход генератора (ток, напряжение и cos φ) и вход дизеля (топливо). Перемножение трех параметров генератора определяет мощность (W_вых) на выходе дизель-генератора. Поскольку количество топлива, подаваемого в дизель (q), пропорционально мощности на входе агрегата, то частное от деления W_вых на q дает величину коэффициента полезного действия. Определив скорости изменения коэффициента полезного действия 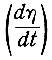и количества топлива 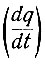и поделив первую на вторую, получим искомую величину 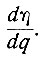Эта величина подается на обычный автоматический регулятор, осуществляющий регулирование по отклонению от нуля напряжения, равного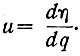

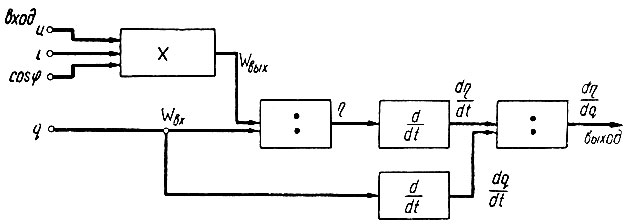
Рис. 6.8. Схема вычисления производной коэффициента полезного действия по количеству топлива

Как следует из рис. 6.8, характерной особенностью всех схем с непосредственным измерением производной является обязательное наличие по крайней мере трех блоков: двух - дифференцирующих и одного блока деления, определяющего частное от результатов дифференцирования.

Экстремальная система с непосредственным измерением производной является достаточно простой. Однако она содержит дифференцирующие блоки, которые, как это уже отмечалось в разделе 2.9, г усиливают высокочастотные помехи. Этот недостаток резко ограничивает область применения систем рассматриваемого типа.