14. Методы поиска экстремума, являющегося функцией нескольких независимых переменных величин

Случай, когда экстремальный параметр (η) является функцией одной переменной величины (q), подаваемой на вход объекта управления, встречается наиболее часто.

Однако иногда величина экстремального параметра оказывается зависимой от двух и более независимых друг от друга величин (x, y, z...), поданных на вход объекта.

Рассмотрим наиболее распространенные методы поиска экстремума для этих случаев.

а) Метод поочередного изменения параметров (метод Гаусса-Зайделя)

Сущность этого метода заключается в поочередном определении частных экстремумов. Иначе говоря, система автоматического управления вначале осуществляет поиск экстремума функции

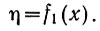
После того как система вышла в область этого экстремума, начинается поиск второго частного экстремума:

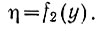
Затем осуществляется выход в область экстремума функции

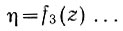
Так продолжается до тех пор, пока не будут найдены все частные экстремумы. После этого система вновь начинает поиск первого экстремума:

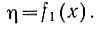
Таким образом, работа системы носит циклический характер, благодаря чему осуществляется поочередное изменение входных параметров.

В случае, когда на входе системы имеется n независимых параметров, исследование ее работы проводится в n-мерном пространстве. Поэтому для упрощения задачи рассмотрим процесс выхода в область экстремума системы с двумя независимыми переменными (x и y).В этом случае характер выхода системы в область экстремума может быть рассмотрен на плоском графике.

Отложим (рис. 6.37) по оси абсцисс одну из поданных на вход системы переменных (х), а по оси ординат - другую (y). Причем, как это делалось ранее (например, рис. 6.23), начало координат перенесем в точку экстремума.

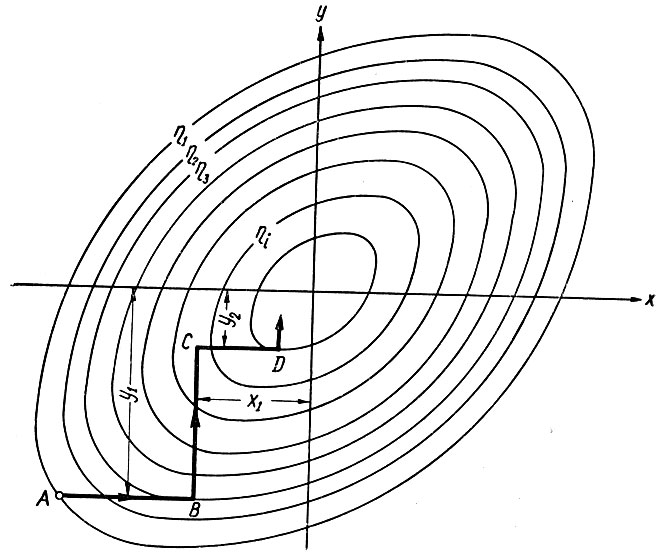
Рис. 6.37. Динамика выхода в область экстремума методом поочередного изменения параметров

Проведем далее на полученной плоскости линии равных значений экстремального параметра: η₁, η₂, η₃, ..., η_i ... При этом, естественно, что

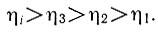
Предположим затем, что в начале работы система находилась в точке А. Тогда движение системы в область экстремума (к началу координат) будет осуществляться следующим образом.

Пусть вначале увеличивается переменная x. Это возрастание будет продолжаться до тех пор, пока при y = y₁ = const не будет достигнут экстремум функции η = f₁(x). В этой точке (В) система переключается на исследование параметра y, после чего начнется его возрастание. В точке С при x = x₁ = const будет достигнут частный экстремум функции η = f₂(y). Затем система вновь осуществляет поиск экстремума функции η = f₁(x), но уже при новом значении y = y₂ = const, более близком к экстремальному, нежели y₁ ...

Так будет продолжаться до тех пор, пока система не выйдет к началу координат.

Метод поочередного изменения параметров удобен тем, что он позволяет использовать самые разнообразные типы экстремальных систем, созданные для поиска экстремума по одному параметру (q). Однако, как видно из рис. 6.37, движение системы в область экстремума происходит далеко не кратчайшим путем.

б) Метод градиента

Этот метод выхода в область экстремума заключается в том, что в системе осуществляется одновременное изменение всех независимых параметров (x, y, z ...). Причем скорость изменения каждого из этих параметров (при непрерывном их изменении) пропорциональна частной производной экстремального параметра (η) по данной переменной:

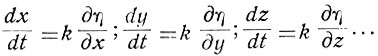(6.45)

В случае же, когда осуществляется дискретное изменение параметров х, y, z ..., величина шага системы по каждому из параметров определяется равенствами

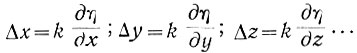(6.46)

Динамика выхода системы в область экстремума для случая, когда в системе имеется два независимых переменных параметра (х и у), показана на рис. 6.38. Как следует из этого рисунка, кривая, характеризующая движение системы, всегда нормальна к кривым равных значений экстремального параметра (η).

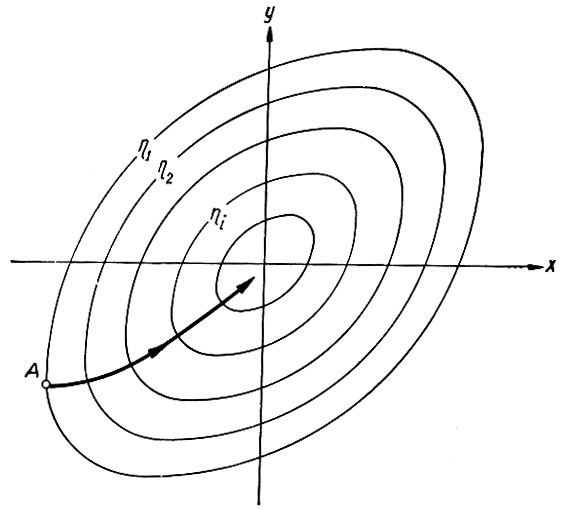
Рис. 6.38. Характеристика выхода системы при использовании метода градиента

Таким образом, при использовании метода градиента величина экстремального параметра возрастает до тех пор, пока система не выйдет в область экстремума. Достоинством этого метода является относительно быстрый выход системы в область экстремума η и малая величина амплитуды рыскания.

в) Метод наискорейшего спуска

Сущность этого метода заключается в том, что в начальной точке (A) определяется направление, нормальное к поверхности η = f(x, y, z ...), соединяющей точки с одними и теми же значениями η и проходящей через точку A. Затем начинается движение системы в направлении этой нормали. Движение системы продолжается до тех пор, пока производная функции η = f(x, y, z ...), взятая вдоль этого направления, не станет равной нулю. После этого вновь определяется направление нормали и происходит движение вдоль нее...

Характер движения системы для случая двух переменных (х и у) показан на рис. 6.39.

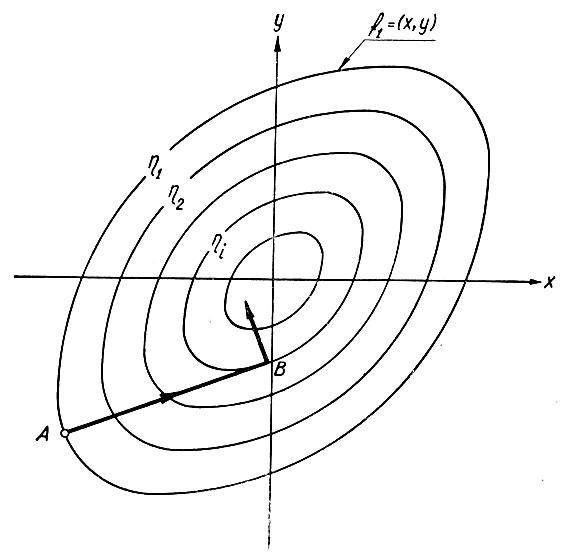
Рис. 6.39. Динамика выхода по методу наискорейшего спуска

Как известно из математики, уравнение нормали, проведенной к кривой f₁(x, y) в точке A, описывается следующей зависимостью:

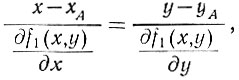(6.47)

где x_А, y_А - координаты точки A;

f₁(x, y) - кривая одинаковых значений η, проходящая через точку A.

После того как направление нормали определено, начинается движение системы вдоль этой нормали. В точке B, в которой экстремальный параметр (η) достигает максимума, вновь определяется направление нормали к кривой одинаковых значений η, проходящей через эту точку. Дальнейшее движение системы происходит уже вдоль нового направления нормали. Так происходит до тех пор, пока система не выйдет к началу координат.

Достоинством метода наискорейшего спуска является относительно малое время выхода в область экстремума.