Глава 2. Радиолокационные методы селекции движущихся целей

2.1. Обнаружение целей на фоне помех

Задача обнаружения целей с помощью РЛС решается с учетом действия на РЛС набора активных и пассивных помех. Причем если активные помехи генерируются не во все промежутки времени, отводимые на обнаружение и перехват целей, то пассивные помехи в виде отражений от поверхности земли и облаков гидрометеоров существуют всегда. Кроме того, в определенные моменты и интервалы времени к этим отражениям от земли могут добавляться отражения от об лаков металлизированных лент или так называемые дипольные помехи.

Если считать, что на вход приемника РЛС воздействуют белый шум с энергетическим спектром G₀ = NKT, пассивная помеха, имеющая при согласовании системы обработки с сигналом энергетический спектр G_пп(f) = K|F(f)|² [где F(f) - спектр сигнала], и, наконец, активная помеха с энергетическим спектром G_ап(f), то суммарный энергетический спектр

В общем случае совокупность мощностей сигналов и помех на входе приемника РЛС можно записать в виде соотношения

где

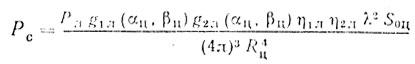
- мощность сигнала, отраженного от точечной цели; Р_ш = NKTΔf - мощность белого шума, отнесенная ко входу приемника;

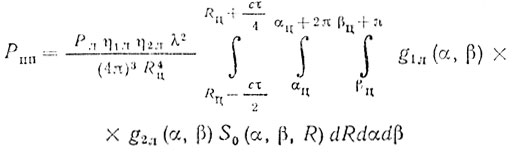
- мощность пассивной помехи, приходящей одновременно с сигналом цели;

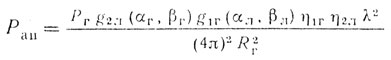
- мощность активной помехи на входе приемника;

S_0ц - средняя эффективная площадь рассеяния цели; S₀(α, β, R) - зависимость эффективной площади рассеяния пассивной помехи (поверхность земли или облако диполей) от координат; g_1л(α, β), g_2л(α, β) - коэффициенты усиления по мощности антенны на передачу и прием; η_1л(α, β), η_2л(α, β) - коэффициент полезного действия фидерного тракта на передачу и прием; Р_л, Р_г - мощности передатчиков РЛС и генератора помех.

Основной особенностью сигналов пассивных помех является то, что борьба с ними невозможна путем увеличения мощности зондирующего сигнала. Из соотношений для Р_с и Р_пп следует

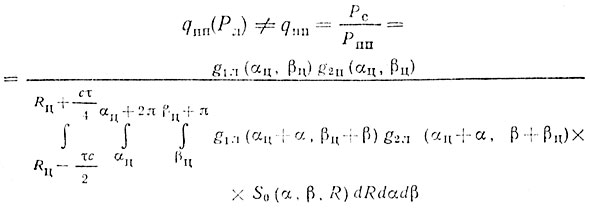
Поскольку сигналы цели и пассивной помехи существуют в один и тот же момент времени, выделение или селекция полезного сигнала на фоне пассивной помехи возможны лишь за счет частотных различий сигнала и пассивной помехи.

В то же время одной из форм борьбы с активными помехами является энергетическая борьба. Действительно, из соотношений для Р_с и Р_ап следует

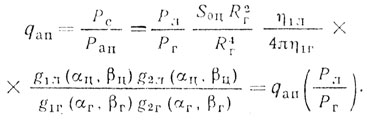
Однако возможна борьба с активными помехами и за счет частотно-временных различий сигнала цели и активной помехи.

Известно [3-7], что линейный фильтр, оптимальный для обнаружения сигнала на фоне гауссовского шума, должен иметь коэффициент передачи, равный

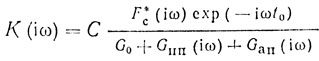(2.1)

При обработке с помощью системы, имеющей такой коэффициент передачи, коррелированные составляющие помехи, а именно пассивная помеха с энергетическим спектром G_пп(iω) и активная помеха с энергетическим спектром G_ап×(iω), обеляются, и на выходе системы обработки имеется белый шум, на фоне которого и производится обнаружение сигнала. Соотношения (2.1) можно преобразовать к виду

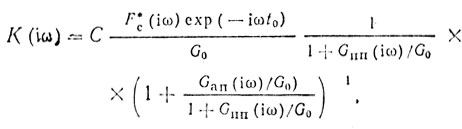(2.2)

соответствующему соединению трех фильтров (рис. 2.1, а), образующих систему последовательно включенных обеляющего и согласованного фильтров.

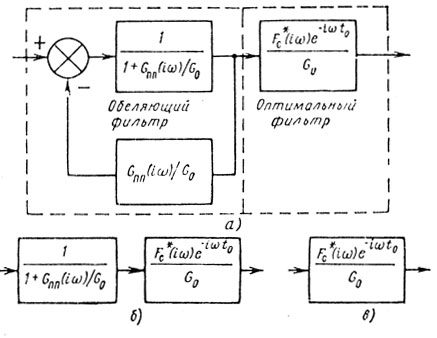
Рис. 2.1

При отсутствии активной помехи (G_ап(iω) ≡ 0) система обработки упрощается (рис. 2.1, б):

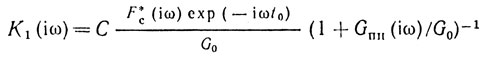
и

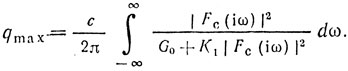
Если пассивная помеха отсутствует (G_пп(iω) = 0), то обработка вырождается в тривиальную обработку сигнала на фоне одного белого шума (рис. 2.1, в):

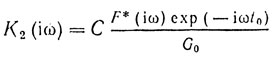
и максимум отношения сигнала к шуму

Таким образом, при известных величинах K₁, G(f) можно максимизировать q согласно соотношению (2.1) путем выбора структуры системы обработки в соответствии с рис. 2.1.

Однако, кроме того, что указанные выше величины обычно заранее не известны, все вышеприведенные соотношения не учитывают реального взаимного расположения цели и помех в пространстве. Для того чтобы решить эту задачу при произвольном расположении цели и помех, удобно перейти к использованию аппарата двумерных корреляционных функций сигнала и помех.

Основы теории зондирующих радиолокационных сигналов достаточно подробно изложены в работах [11-13], где для оценки свойств зондирующего сигнала используется двумерная корреляционная функция

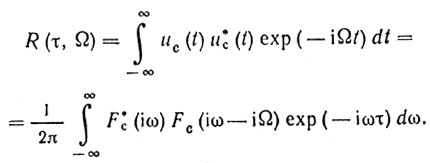
Нормируя это выражение относительно максимума, получаем

Обозначив U₂(t) = U_mU(t) и F_c(iω) = U_mF(iω), получим

Мерой разрешения сигналов по времени и частоте (дальности и скорости) являются величины:

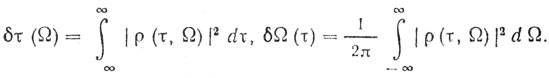
Так как нормированная двумерная корреляционная функция ρ описывает поведение отклика сигнала на выходе оптимальной системы обработки, то с помощью функции ρ(τ, Ω) можно определить отношение мощностей полезного сигнала и помех [4, 5], зная расположение цели в пространстве, распределение интенсивности пассивной помехи по времени и частоте, а также свойства сигнала активной помехи. При этом необходимо учитывать неоднородность помехи по пространству (времени запаздывания τ = x) с помощью функции ρ(x, τ, Ω). Тогда

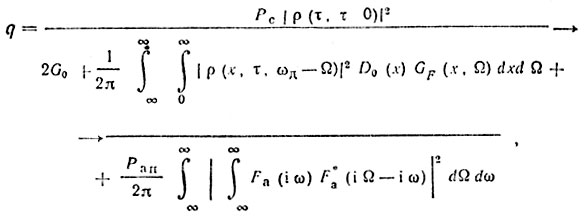(2.3)

где ρ(x, τ, Ω) - двумерная корреляционная функция с учетом ее зависимости от времени запаздывания; D₀(x) - функция распределения интенсивности помех по дальности; G_F(x, Ω) - энергетический спектр флуктуации пассивной помехи; F_a(iω) - энергетический спектр активной помехи.

Если объединить D₀(x) и G_F(x, Ω) в так называемую функцию распределения интенсивности (энергии) помехи на плоскости τ, Ω, то получим

Тогда при F_a(iω) = 0

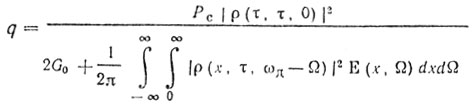
Трудности технической реализации радиолокаторов с оптимальной обработкой сигналов и жесткие требования к качеству селекции, движущихся целей привели к тому, что в радиолокаторах СДЦ не всегда используется оптимальное построение.

В РЛС СДЦ для установления различий параметров отраженных и зондирующих сигналов опорный сигнал, с которым сравниваются отраженные сигналы, должен быть связан по сравниваемому параметру с зондирующим сигналом. Когерентные методы используют при сравнении фазу и частоту заполнения (несущей) радиосигналов, некогерентные методы - огибающую сигналов (амплитуду), период (частоту) повторения, кадровые различия сигналов. В последнем случае имеют дело с видеосигналами.

Установим понятие когерентности сигналов или колебаний. Когерентными сигналами или колебаниями называют такие сигналы или колебания, у которых на интервале наблюдения Т_н существует жесткая связь любых частей колебаний Когерентными могут быть два или несколько колебаний, у которых имеется жесткая временная связь различных участков колебания. Иногда жесткую связь отдельных "кусков" одного и того же колебания или сигнала называют автокогерентностью.

Истинно когерентные сигналы имеют бесконечный интервал когерентности или по крайней мере больший интервал наблюдения. Если интервал когерентности сигналов ограничен или меньше интервала наблюдения, то такие сигналы называют почти когерентными или условно когерентными. Однако в радиолокации понятие когерентности сигналов расширяется. Когерентными обычно называют сигналы, у которых имеется произвольная жесткая функциональная связь фазы высокочастотного заполнения (несущего колебания) любых частей сигнала в пределах интервала когерентности. Следовательно, когерентные сигналы могут иметь любую модулирующую функцию и не должны иметь лишь случайных изменений или хаотических скачков фазы высокочастотного заполнения.