2.3. Когерентный метод непрерывного излучения при использовании модуляции

Измерение дальности движущихся целей возможно, как было показано выше, при использовании нескольких непрерывных сигналов разной частоты или спектральных составляющих модулированного сигнала. При модуляции гармонического сигнала по одному из параметров спектр сигнала состоит из ряда гармоник, смещенных относительно несущего колебания и относительно друг друга на частоту модуляции. Число гармоник в спектре и их амплитуды будут определяться глубиной и законом модуляции. Выбор частоты модуляции зависит от пределов однозначного от счета дальности и от ширины спектра мешающих отражений.

Рассмотрим работу РЛС непрерывного излучения, использующей гармонический закон частотной модуляции (рис. 2.9). На выходе смесителя при любой форме сигналов образуется так называемый преобразованный сигнал, являющийся биениями прямого и отраженного колебаний. Воспользуемся соотношением (2.6), полученным для этого случая.

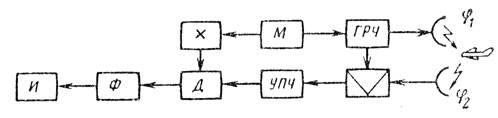
Рис. 2.9

При гармоническом законе модуляции

где ω₀ - несущая частота колебания; Δω - девиация частоты; Ω_М - частота модуляции.

Фазы прямого и отраженного сигналов φ₁ и φ₂ находятся из соотношений:

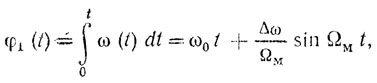(2.13)

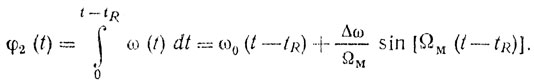(2.14)

Разность фаз прямого и отраженного сигналов можно представить в виде

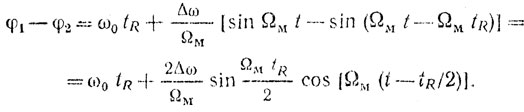(2.15)

Обозначим

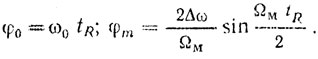(2.16)

Тогда выражение (2.6) запишется в форме

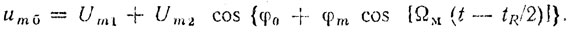
Это выражение можно преобразовать [1]:

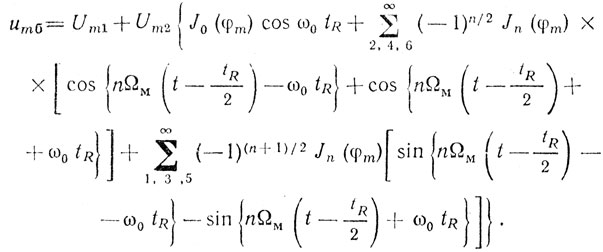(2.17)

Для неподвижной цели t_R = const и спектр преобразованного сигнала состоит из гармоник частоты модуляции nΩ_M, амплитуда которых зависит от дальности цели, так как

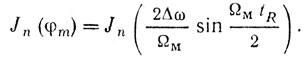
При Ω_Mt_R < 0,5 можно считать, что sin(Ω_Mt_R/2) ≈ Ω_Mt_R/2 и поэтому J_n(φ_m) ≈ J_n(Δωt_R).

Для движущейся цели t_R = tR₀ + 2υ_rt/c, поэтому спектр изменяется:

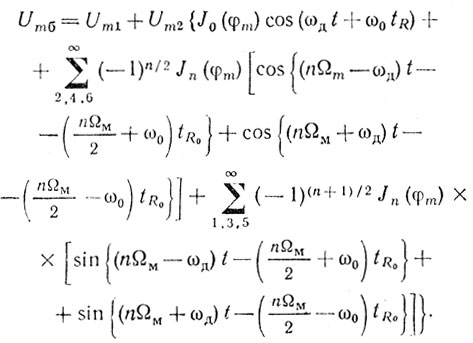(2.18)

Видно, что спектр преобразованного сигнала движущейся цели состоит из гармоник nΩ_M ± ω_д.

Для селекции движущейся цели из спектра преобразованного сигнала с помощью селективного усилителя промежуточной частоты (УПЧ) достаточно выбрать одну из составляющих nΩ_M ± ω_д. Выбором соответствующего n > 1 можно при данной частоте модуляции без значительного энергетического проигрыша избежать влияния шумов пере датчика и определить скорость движущейся цели. Для этого гармоника nΩ_M ± ω_д сравнивается после усиления в УПЧ, настроенном на частоту nΩ_M, с гармоникой частоты модуляции nΩ_M. На выходе элемента сравнения детектора (Д) после фильтрации остается лишь сигнал частоты ω_д (рис. 2.10).

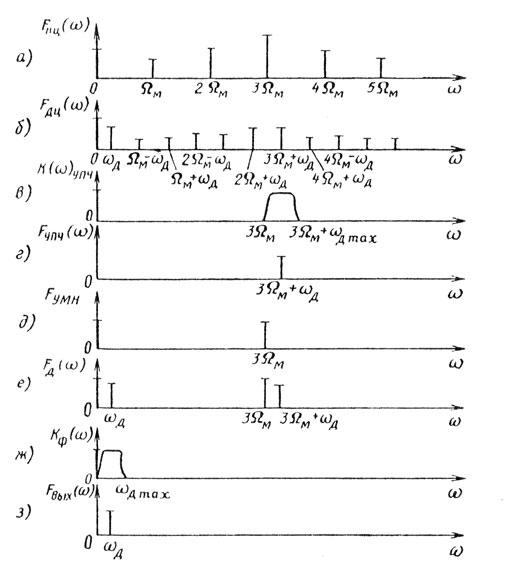
Рис. 2.10

Усложнив систему, можно обеспечить при известной частоте f_д измерение дальности цели R. Действительно, пусть

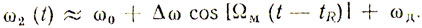
Тогда

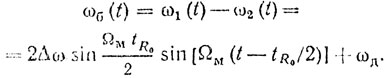(2.19)

При t_R0 << 2π/Ω_M можно считать, что

Вычислив среднюю частоту биений для двух полупериодов модуляции, получим для первого полупериода

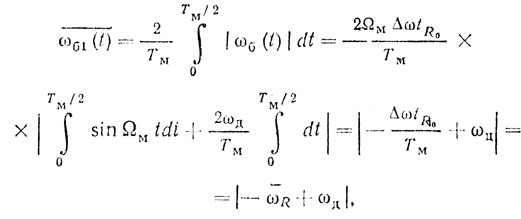(2.20)

где 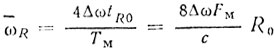- средняя круговая частота, пропорциональная дальности цели.

Производя аналогичные вычисления, для второго полупериода модуляции получаем

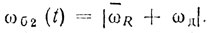(2.21)

Если известно ω_д, можно, усредняя частоты биения на отрезках T_M/2, вычислять значения ω_R, а значит определять R.

Рассмотрим теперь РЛС непрерывного излучения [1.51] с частотной модуляцией по закону меандра (рис. 2.11). В этой РЛС частота передатчика скачками меняется между двумя значениями ω₀ и ω₀ + ω_пч с низкой частотой Ω_M. Приемник супергетеродинного типа работает на промежуточной частоте ω_пч, и частота гетеродина также изменяется в пределах ω₀ и ω₀ - ω_пч.

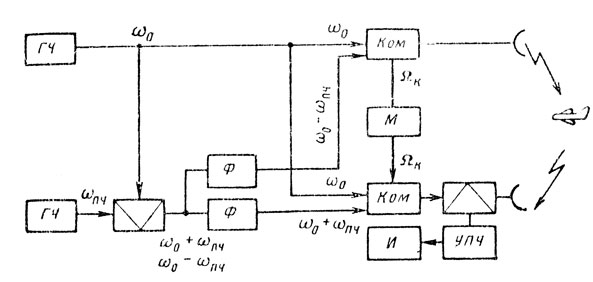
Рис. 2.11

Изменение частот сигналов в данной системе показано на рис. 2.12. Очевидно, импульсы в канале промежуточной частоты будут наиболее широкими, если время запаздывания кратно нечетному числу половин периода модуляции:

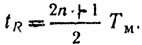
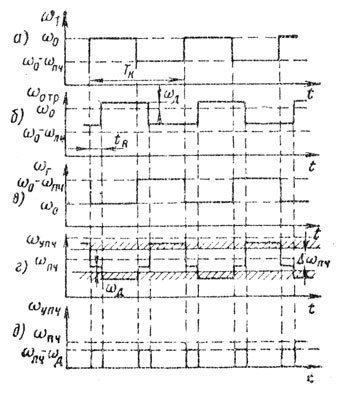
Рис. 2.12

В этом случае в канале УПЧ будет непрерывный сигнал частоты ω_пч - ω_д. Это время запаздывания называется оптимальным t_Rопт и соответствует оптимальной дальности до цели R_опт. И, наоборот, при времени запаздывания, кратном периоду модуляции сигнала t_R = nТ_М, импульсы в канале УПЧ отсутствуют. Таким образом, при селектировании сигнала одной цели, меняя Т_м, можно подобрать наивыгоднейший энергетический режим для обнаружения этой цели.

Для разделения сигналов целей, имеющих одинаковую радиальную скорость, но различную дальность, можно использовать линейную модуляцию частоты внутри каждой половины меандра. В этом случае сигналы целей с разных дальностей будут иметь различные разностные частоты ω_p = ω_д - 2ω₀t_R/Т_M, большие или меньшие по сравнению с сигналом цели, находящейся на оптимальной дальности (рис. 2.13).

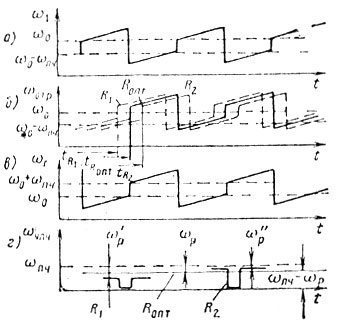
Рис. 2.13

Качество фильтрации или, что то же самое, качество селекции сигналов движущихся целей на фоне мешающих отражений от поверхности земли зависит от соотношения частоты модуляции Ω_M, доплеровской частоты движущейся цели ω_д и диапазона доплеровских частот мешающих отражений ±ω_{д max}.

В нашем случае для повышения качества селекции необходимо вы полнить соотношение

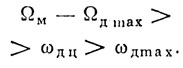
При этом спектральные составляющие сигнала движущейся цели не будут совпадать со спектром помехи.