7.3. Адаптация к доплеровской поправке и форме спектра помехи

Измерение доплеровского набега фазы за период повторения может осуществляться различным образом, на пример [82] используя фазовый детектор или иной фазометр вместо вычитающего устройства в системе череспериодного вычитания на промежуточной частоте (рис. 7.11) Среднее значение косинуса набега фазы может затем использоваться для ввода поправок в частоту гетеродина для компенсации движения пассивной помехи [82] или для управления безынерционным электронным фазовращателем с той же целью [8].

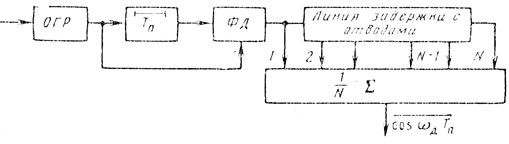
Рис. 7.11

Если рассмотреть векторную диаграмму сигнала пассив ной помехи в двух соседних периодах повторения (рис. 7.12), то, используя формулы косинуса и синуса разности углов φ₁ и φ₂, можно получить соотношения:

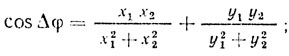
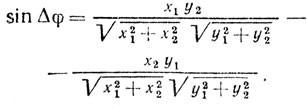
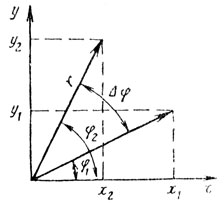
Рис. 7.12

Здесь x₁, x₂, y₁, y₂ - сигналы помехи в двух соседних периодах повторения в квадратурных каналах обработки.

Что касается формы энергетического спектра помехи или корреляционной функции помехи, то основными аппроксимациями их являются гауссовский или резонансный спектр и соответствующие им гауссовская или экспоненциальная форма нормированной функции корреляции [23]. При гауссовской аппроксимации спектра имеем:

При резонансной аппроксимации спектра имеем:

Как правило, предпочитают производить оценку искомых параметров путем измерений параметров нормированной функции корреляции. Причем наиболее просто это осуществить в предположении марковости помехи и сигнала, когда необходимо оценить межпериодную нормированную функцию корреляции. Для этих целей может быть использована связь мощностей помехи на входе и выходе системы череспериодного вычитания и суммирования [8] (рис. 7.13).

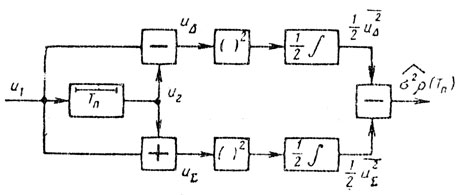
Рис. 7.13

Поскольку u₁ = u(t), а u₂ = u(t - T_п), то u_Δ = u(t) - u(t - T_п), а u_Σ = u(t) + u(t - Т_п). Если определить u¯²_Σ и u¯²_Δ, то получим:

тогда

На рис. 7.13 показана структурная схема устройства оценки межпериодной нормированной функции корреляции. Зная ρˆ(T_п), можно определить параметр формы спектра помехи σ_fп. Например, при экспоненциальной форме корреляционной функции

а при гауссовской форме

оценки максимального правдоподобия дисперсии и нормированной функции корреляции для стационарных в пространстве помех [29] могут вычисляться по соотношениям:

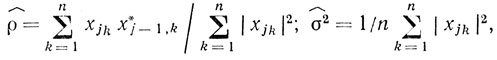(7.7)

где n - число элементов разрешения (по дальности или азимуту), по которым идет усреднение, характеристик помехи.

Если модуль нормированной функции корреляции близок к единице (ρ → 1), то замена его на единицу и учет только доплеровского набега фазы приводит к ухудшению подавления помехи и потерям 0,5 (1 + ρ²).

Оценку максимального правдоподобия доплеровского набега фазы φˆ можно получить по алгоритму

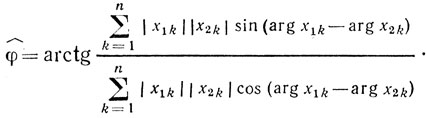(7.8)

В [8] описана система ввода поправок на среднюю частоту спектра помехи с помощью управляемого генератора (Г) и быстродействующего фазовращателя (БФВ) (рис. 7.14). Сигнал с выхода фазового детектора (ФД) подается на схему выборки и фиксации (СВФ), отпираемую отпирающим импульсом (ОИ) на участке дистанции, где имеются сильные пассивные помехи (начало дистанции). По этим сигналам подстраивается генератор для выполнения условия Т₃ω2 = n2π, т. е. осуществляется компенсация непостоянства длины линии задержки. Вторая цепь обратной связи, состоящая из стробирующей схемы (СС), отпираемой и запираемой ОИ и запирающим импульсом (ЗИ), и БВФ, служит для компенсации скорости облаков дипольных помех или гидрометеоров.

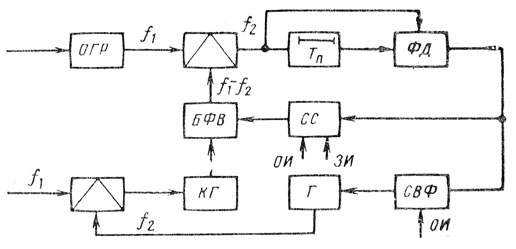
Рис. 7.14

В [86] приведены данные по моделированию разомкнутой адаптивной системы СДЦ, компенсирующей фазовый набег пассивной помехи за период повторения. Общая схема построения системы показана на рис. 7.15, где используется ЧПВ с весами W = -1; W₂ = W = ехр (i2πf_дT_п).

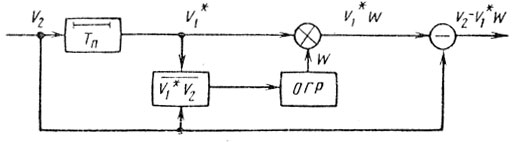
Рис. 7.15

Для автоматического представления весов вычисляется корреляционная функция помех в виде среднего значения выборок помехи, разделенных интервалом в период повторения:

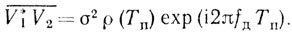
Используя затем когерентный ОГР, получаем оценку

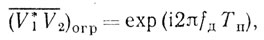
которая является весовым множителем W в адаптивной системе. Для получения практически точной оценки усреднение обычно производится в М элементах дальности (М > 4), при этом необходимо отношение мощности помехи к шуму не менее 2 дБ.

После формирования весового множителя W осуществляются компенсация эффекта движения помехи V*₁W и обычное череспериодное вычитание V₂ - V*₁W = ΔV.

Результаты сравнения по коэффициенту улучшения адаптивной разомкнутой системы (рис. 7.15) и однократной системы ЧПВ; работающей в оптимальных условиях, в зависимости от межпериодной нормированной функции корреляции помехи и отношения помеха-сигнал по мощности q_пш приведена на рис. 7.16 (при этом W формировалась по четырем выборкам). Моделирование показало, что у системы, (рис. 7.15) отсутствует эффект кромки помехи и что потери при вобуляции периода не превышают 1,5-2 дБ, а потери чувствительности при отсутствии помех составляют 1,5-2 дБ.

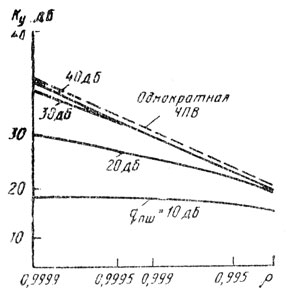
Рис. 7.16

В системе СДЦ с корреляционными обратными связями (КОС) [5, 23, 85] происходит череспериодное вычитание с весовыми коэффициентами, пропорциональными нормированной функции межпериодной корреляции помехи (рис. 7.17). Формирование весового коэффициента K осуществляется умножением выходного сигнала Δu на входной сигнал u₁ и интегрированием произведения. Затем полученный весовой коэффициент К с учетом коэффициента усиления β разомкнутой петли обратной связи умножается на входной сигнал и вычитается из задержанного сигнала u₂. Составляя уравнения функционирования схемы (рис. 7.17):

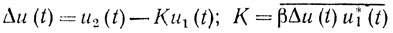(7.9)

и решая совместно систему, получаем

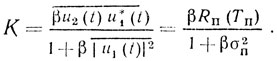(7.10)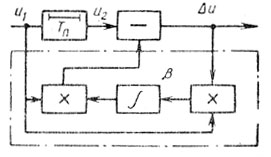

Рис. 7.17

Если считать u₁ и u₂ помехой, то остатки вычитания будут

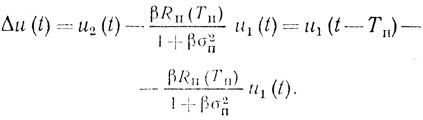(7.11)

Полагая β >> 1 и u_m1(t - T_п) ≈ u_m1(t), из (7.11) получаем Δu ≈ u_m1[1 - ρ_п(Т_п)] и при значительной нормированной функции корреляции ρ_п(T_п) → 1 остаток помехи Δu → 0. Основным достоинством системы с КОС является самонастройка или адаптация системы на характеристики помехи, в результате чего она отрабатывает как изменение скорости движения помехи, так и изменение ширины спектра (корреляционной функции) помехи в схеме с двумя квадратурными каналами.

Анализ устройства подавления пассивных помех с корреляционными обратными связями [5, 23], изображенного на рис. 7.17, показывает, что в установившемся режиме коэффициент передачи устройства может быть записан в виде

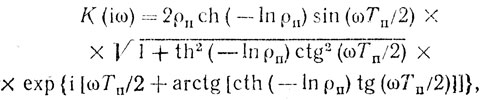(7.12)

где ρ_п - нормированная функция межпериодной корреляции пассивной помехи. Следовательно, АЧХ определяется соотношением

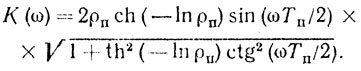(7.13)

При ρ_п → 1 выражение (7.13) стремится к характеристике системы однократного вычитания К(ω) → 2 sin (ωТ_п/2). При ρ_п → 0 характеристика превращается в равномерную: К(ω) → 1.

Наиболее общей задачей при синтезе адаптивных систем СДЦ является синтез системы декорреляции помехи или обеляющего фильтра с использованием статистик помехи, инвариантных к изменениям характеристик помехи, таких как ее мощность, ширина спектра и доплеровский. набег фазы. В ряде работ [4, 28, 29] для решения этой задачи было предложено использовать T²-тест Хотеллинга. Этот тест считается равномерно наиболее мощным инвариантным критерием для проверки гипотез о величине вектора средних значений многомерной нормальной совокупности. Он построен на множестве инвариантных статистик, распределение которых при гипотезе отсутствия сигнала или равенстве вектора средних нулю не зависит от корреляционной матрицы В и инвариантно к преобразованиям G₁, G₂ и G₃. Преобразование G₁ дает добавку в виде произвольной постоянной величины к каждой координате вектора выборочных значений х; преобразование G₂ обеспечивает операцию х' = С₁х, где C₁ - ортогональная матрица, а G₃ определяет изменение масштаба х" = C₂x₁, где С₂ - константа. Отмеченные преобразования определяют изменения доплеровского набега фаз, модуля нормированной корреляционной функции (ширина спектра) и мощности помех [29]. Следовательно, инвариантная статистика нечувствительна к этим изменениям параметров помехи.

Алгоритм оптимального обнаружения с использованием инвариантной статистики записывается следующим образом:

где Т² = x^*тВˆ^-1; T²₀ - порог обнаружения; В^-1 - матрица, обратная корреляционной; "*" - знак комплексной сопряженности; "т" - знак транспонирования; "∧" - знак оценочного значения; Вˆ^-1 - оценка максимального правдоподобия обратной корреляционной матрицы помехи.

Если заменить матрицу Вˆ^-1 на произведение верхней и нижней треугольных матриц, то

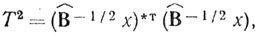
где Вˆ^-1/2 - нижняя треугольная матрица. Тогда операцию в круглых скобках можно трактовать как процесс обеления пассивной помехи [31].

В случае детерминированных сигналов достаточной статистикой можно считать W-статистику:

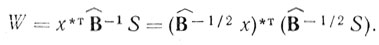(7.15)

Первая скобка дает обеление пассивной помехи, а вторая - преобразует вектор сигнала S. Таким образом, алгоритм адаптивного инвариантного к изменениям помехи обнаружения сигнала реализуется с использованием двух основных устройств: устройства оценки обратной корреляционной матрицы помех Вˆ^-1 =||bˆ^-1_jk|| и обеляющего фильтра с весами при обработке, определяющимися в соответствии с оценками bˆ^-1_jk. Известно [4, 30], что элементы обратной корреляционной матрицы помехи b^-1_jk при представлении последней марковским процессом (последовательностью) вычисляются по алгоритму

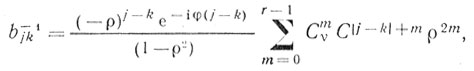(7.16)

где С^m_ν = (^ν_m) - биномиальный коэффициент; ν - связность марковской последовательности; ρ, φ - модуль и аргумент межпериодной функции корреляции.

Поскольку b^-1_jk = b^-1_{p-j+1, p-k+1}, а при |j - k| > ν b^-1_jk = 0, r = j для j ≥ k и r = k для j < k, то обратная корреляционная матрица В^-1 имеет ленточно-диагональную структуру, при которой существуют (отличная от нуля) главная диагональ и ν поддиагоналей выше и ниже главной. В этом случае статистика Хотеллинга вырождается в алгоритм

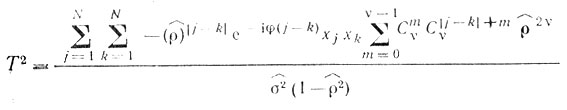(7.17)

где x_j - j-й отсчет входной реализации; σˆ² - оценка дисперсии помехи.

Если начало и конец пачки не фиксированы (плавный обзор пространства), то можно использовать модифицированную статистику или упрощенный алгоритм [29, 30]

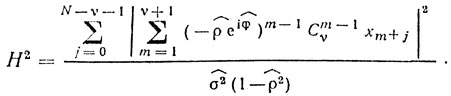(7.18)

Этот алгоритм, как показано в [30], является инвариантным к доплеровскому набегу фазы и незначительно проигрывает по средней мощности остатков помех ига выходе строгому алгоритму T²-статистики.