8.2. Скоростные характеристики устройств СДЦ с вобуляцией периода повторения

Простейшим примером вобуляции может служить последовательная смена периода повторения зондирующих импульсов Т_П1, Т_П2, Т_П1, Т_П2. Для получения более гладкой скоростной характеристики в современных РЛС СДЦ, используют большее число периодов повторения и закон вобуляции в этом случае имеет вид

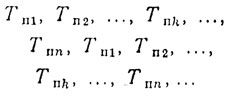
Прежде чем переходить к нахождению скоростной характеристики фильтров СДЦ при вобуляции периода по закону, описанному выше, рассмотрим функцию f(t), временная дискретизация которой осуществляется посредством неравномерных выборок (рис. 8.2, а). Последовательность выборок формируется с помощью так называемого ядра вобуляции, состоящего из n неравномерных временных интервалов Т_П1, Т_П2, ..., Т_Пk, ..., Т_Пn, которое повторяется с постоянным периодом. Назовем его периодом вобуляции

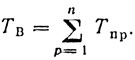(8.2)

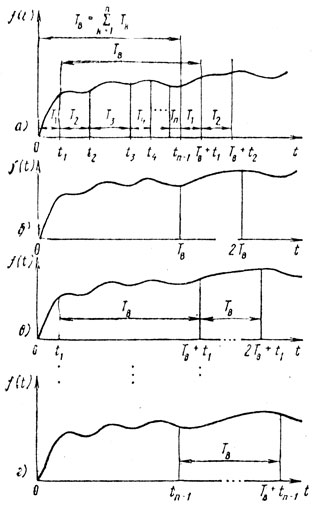
Рис. 8.2

Момент появления любой выборки определяется соотношением

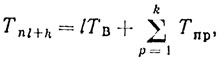(8.3)

а внутри ядра

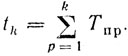
Описанную выше последовательность неравномерных выборок можно рассматривать как суперпозицию n (по числу выборок, входящих в ядро вобуляции) периодических последовательностей с одним и тем же периодом, равным T_в (рис. 8.2, б, в, г). Когда такая последовательность поступает на вход линейного фильтра, то выходной сигнал в момент времени t_k также может рассматриваться как супер позиция откликов фильтра на воздействие n периодических последовательностей. А для определения отклика на воздействие всего сигнала необходимо провести вторичное суммирование по числу выборок ядра n.

Идея такого представления вобулированной последовательности импульсов при анализе скоростных характеристик режекторных фильтров была впервые высказана в работе [87] и нашла свое дальнейшее развитие в [89-92]. Она также была использована при анализе спектрально-корреляционных свойств зондирующего сигнала и оценке эффективности фильтров СДЦ с переменным периодом повторения [90-92].

Применяя изложенный выше метод анализа при воздействии на нерекурсивный режекторный фильтр гармонического сигнала со случайной начальной фазой, равномерно распределенной в интервале [0,2π], получаем следующее соотношение для расчета скоростной характеристики при вобуляции периода повторения [88, 89]:

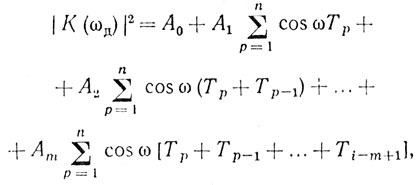(8.4)

где m - порядок фильтра; А - нормированные весовые коэффициенты.

Значения нормированных весовых коэффициентов для нерекурсивных режекторных фильтров до 4-го порядка приведены в табл. 8.1.

Таблица 8.1

Наличие нескольких периодов повторения усложняет вид скоростной характеристики режекторных фильтров, которая теперь является результатом интерференции нескольких характеристик с различными периодами. Если при постоянном периоде повторения первый нуль скоростной характеристики определялся на частоте f = Т^-1_п (или ω = 2π/T_п), то в случае вобуляции периода повторения первый нуль будет на частоте f = ΔТ^-1 (или ω = 2π/ΔT), где ΔT - наибольший общий делитель для всех периодов Т_пn ядра.

Общие закономерности формирования скоростных характеристик наиболее наглядно можно проиллюстрировать на примере режекторного нерекурсивного фильтра первого порядка, для которого в соответствии с (8.4)

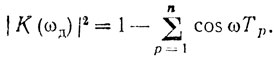(8.5)

В этом случае, если каждый последующий период в ядре увеличивается по сравнению с предыдущим на ΔT, уравнение (8.5) можно привести к виду

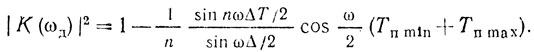(8.6)

Очевидно, что частотно-интерференционную картину скоростной характеристики определяют выражением

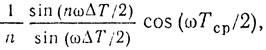
где T_{п ср} = 0,5 (Т_{п min} + Т_{п max}).

Сомножитель 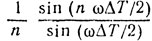как бы модулирует по амплитуде сигнал cos (ωT_{п ср}/2), характеризуя огибающую экстремальных значений скоростной характеристики. На рис. 8.3 приведена скоростная характеристика для n = 5 (сплошная линия) и ее огибающая (штриховая линия).

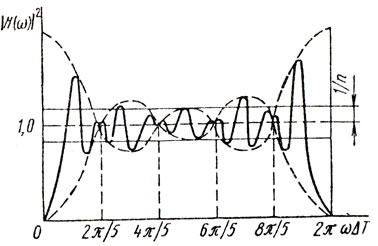
Рис. 8.3

Из рисунка видно, что глубина пульсаций в полосе пропускания зависит от числа периодов, используемых при вобуляции, т. е. размера ядра. При этом наибольшее значение имеет глубина первого провала (первого нуля). В табл. 8.2 приведены расчетные значения глубины первого нуля (в дБ) для нерекурсивного фильтра первого порядка в зависимости от числа периодов n и коэффициента расширения полосы фильтра, равного отношению Т_{п ср}/ΔT.

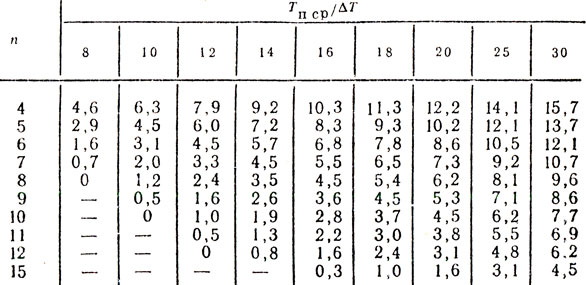
Таблица 8.2

Анализ данных, приведенных в табл. 8.2, позволяет сделать некоторые выводы о зависимости скоростной характеристики нерекурсивного первого порядка фильтра от n и ΔT, которые справедливы и для фильтров более высокого порядка. Увеличение отношения T_{п ср}/ΔT при фиксированном значении n приводит к росту глубины первого нуля скоростной характеристики, т. е. к повышению ее неравномерности и, следовательно, к снижению эффективности режекторного фильтра. Увеличение числа периодов снижает глубину первого нуля, но структура приемного тракта РЛС становится более сложной.

При использовании нерекурсивных фильтров более высокого порядка, как следует из соотношения (8.4), частотно-интерференционная картина значительно усложняется, в результате чего устранение провалов в скоростной характеристике требует применения специальных мер при формировании вобуляционного ядра.

Скоростная характеристика нерекурсивного фильтра второго порядка становится более равномерной, а глубина первого нуля уменьшается, если использовать перестановки периодов повторения внутри вобуляционного ядра таким образом, чтобы суммы следующих друг за другом соседних периодов отличались на ΔT, например: 15ΔT, 18ΔT, 16ΔT, 19ΔT, 17ΔT, 20ΔT.

Для фильтров третьего и более высокого порядка такая процедура не приводит к желаемому результату [8, 89].

Как уже отмечалось, требования обеспечения заданной ширины скоростной характеристики и минимизации глубины первого нуля противоречивы. Это противоречие устраняется увеличением числа используемых периодов, что не всегда возможно в силу аппаратурных ограничений. Выходом из этого положения является подбор соотношений между периодами повторения ядра вобуляции. Так можно выбрать в качестве наибольшего общего делителя не величину ΔT, а 2ΔT. В этом случае возникает дополнительный минимум в точке π/ΔT, который можно компенсировать, заменив один из периодов ядра вобуляции T_пi на T'_пi. В этом случае в соотношении (8.5) для фильтра первого порядка появится дополнительный член (cos ωT_пi - cos ωT'_пi) = 2 sin ω ^T'_пi-T_пi/₂ sin ω (T'_пi + T_пi)/2. Если ωT'_пi - ωT_пi = ΔT, огибающая, соответствующая этому члену, будет равна нулю на частоте ω₀ = 2π/ΔT, т. е. в точке, совпадающей с заданной первой "слепой" скоростью, а нуль основной характеристики на частоте π/ΔT будет скомпенсирован максимальным значением дополнительного члена. Кроме этого, скоростную характеристику в окрестности нуля можно улучшить подбором периода T'_пi.

Описанная выше процедура иллюстрируется на рис. 8.4 [89]. Здесь ядру 12ΔT, 16ΔT, 14ΔT, 18ΔT соответствует скоростная характеристика, изображенная на рис. 8.4, а. Это ядро можно заменить ядром 12ΔT, 16ΔT, 13ΔT, 18ΔT (рис. 8.4, б) или ядром 12ΔT, 16ΔT, 15ΔT, 18ΔT (рис. 8.4, в). В обоих случаях один из периодов изменяется на ΔT, что обеспечивает компенсацию нуля на частоте π/ΔT, но в первом случае (рис. 8.4, б) благодаря использованию периода длительностью 13ΔT глубина первого нуля меньше.

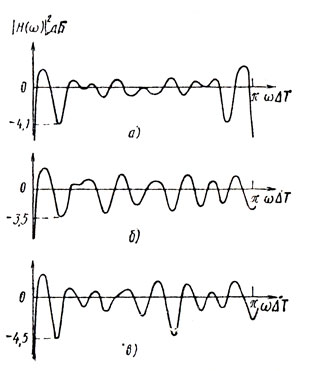
Рис. 8.4

В качестве второго при мера, иллюстрирующего процедуру выбора периодов повторения при вобуляции на основе анализа частотно-интерференционной картины, рассмотрим ядро из пяти периодов 36ΔT, 45ΔT, 39ΔT, 48ΔT, 42ΔT, т. е. с разницей, равной 3ΔT. В этом случае скоростная характеристика принимает нулевые значения в точках ω = 2π/3ΔT и ω = 4π/3ΔT. Компенсацию этих нулей можно осуществить путем изменения любого периода на величину ΔT или 2ΔT.

Выражение для расчета скоростной характеристики в соответствии с (8.5) имеет вид

Компенсировать нули можно, заменив период длительностью 45ΔT на период 47ΔT, что приведет к появлению в (8.7) нового слагаемого 2 sin ωΔT sin 46ωΔT. Нули также компенсируются, если период 48ΔT заменить периодом 46ΔT, что связано с появлением слагаемого 2 sin ωΔT × sin 47ωT. Кроме того, можно уменьшить период 39ΔT до 38ΔT и увеличить период 42ΔT до 43ΔT. Эти две замены добавят в уравнение (8.7) соответственно слагаемые 2 sin (ωΔT/2) sin (77ωΔT/2) и 2 sin (ωΔT/2) sin (85ωΔT/2). На рис. 8.5 приведена скоростная характеристика для случая, когда соотношения между периодами равны 36ΔT, 47ΔT, 38ΔT, 46ΔT, 43ΔT.

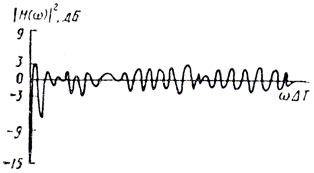
Рис. 8.5

Многочисленные эксперименты позволили выработать ряд общих рекомендаций (полезных разработчикам при выборе ядра вобуляции) с учетом требований, предъявляемых к скоростным характеристикам нерекурсивных режекторных фильтров [8, 88, 89]. При решении вопроса о том, какой из периодов следует изменить, необходимо избегать повторения разности, большей чем ΔT, так как это приводит к появлению глубоких про валов в скоростной характеристике. Для улучшения скоростной характеристики в области малых значений Од, целесообразно применять положительную коррекцию (+ΔT) к длинным периодам и отрицательную (-ΔT) к коротким. Смежные соседние периоды целесообразно изменять так, чтобы сблизить их, например 48ΔT заменить на 46ΔT, а 45ΔT на 47ΔT. Перечисленные рекомендации справедливы и для ядер вобуляции с большим числом периодов повторения.

Определенным недостатком описанного выше метода формирования требуемой скоростной характеристики является то, что все его рекомендации не подкреплены теоретическими выкладками, которые обосновали бы их оптимальность (или квазиоптимальность), а также то, что они строились на основе общего для всех периодов повторения наибольшего делителя ΔT. В связи с этим необходимо отметить следующее. В [89] описывается попытка оптимизации ядра вобуляции на основе критерия наименьшего квадрата отклонения скоростной характеристики от среднего уровня в рабочей полосе частот. Процедура оптимизации не дала заметного улучшения скоростной характеристики. И, как отмечается, все попытки усовершенствовать этот метод оказались безуспешными