8.3. Эффективность систем СДЦ с переменным периодом повторения

Повышение эффективности обнаружения движущихся целей в окрестности "слепых" скоростей за счет изменения периода повторения обычно связывают с улучшением частотных характеристик режекторных фильтров. Однако единственной причиной, по которой происходит рост эффективности систем СДЦ, является изменение спектрально-корреляционных свойств сигнала и помехи в результате вобуляции периода повторения. Поэтому, прежде чем приступить к определению таких параметров, характеризующих качество работы систем СДЦ, как коэффициенты подавления и улучшения, а также глубины первого нуля скоростной характеристики |H_м(1/Т_{п ср})|², необходимо детально проанализировать спектрально-корреляционные свойства последовательности зондирующих импульсов с вобуляцией периода повторения.

За основу может быть взят принцип формирования сигнала с переменным периодом повторения, изложенный в § 8.2. Напомним, что в этом случае имеется ядро вобуляции, состоящее из n импульсов, которое повторяется с периодом вобуляции T_в = Σⁿ_k=1 T_пk, где T_пk - интервалы между импульсами. Используя такое представление последовательности импульсов с переменным периодом повторения, в [87] была разработана методика анализа ее спектральных свойств, на основе которой были получены простые соотношения для оценки эффективности систем СДЦ с вобуляцией периода повторения [90-92].

При формировании модели последовательности импульсов с переменным периодом предполагалось, что отраженный сигнал в случае постоянного периода можно записать как

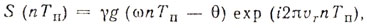(8.8)

где Т_п - период повторения; γ = A exp (iφ) - множитель, характеризующий амплитуду и фазу сигнала, отраженного от цели; g( ) - коэффициент усиления антенны с учетом прохождения сигнала в двух направлениях; ω - скорость обзора; θ - азимут цели; υ_r - радиальная скорость цели.

Пачка отраженных импульсов промодулирована по амплитуде диаграммой направленности и имеет максимум при ωnТ = θ. Для простоты можно положить θ = 0. Считая, что длительность зондирующего импульса много меньше периода доплеровской частоты, последовательность импульсов можно представить в виде

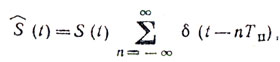(8.9)

где

Тогда при двухпериодной вобуляции сигналы появляются в моменты времени 0, Т_п - ΔT, 2Т_п, 3Т_п - ΔТ, 4Т_п, ... (ΔТ может быть и со знаком "плюс") и, следовательно, мы имеем последовательность выборок S(0), S(Т_п - ΔT), S(2Т_п), S(3Т_п - ΔТ), которую можно представить как сумму двух выборок: S(t) в моменты 0,2Т_п, 4Т_п, 6Т_п, ... и S(t - ΔT) в моменты Т_п, 3Т_п, 5Т_п, ... Соотношение (8.9) запишется следующим образом:

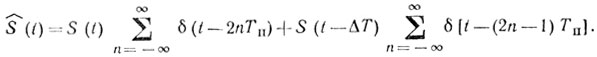(8.11)

Когда ядро вобуляции содержит М импульсов

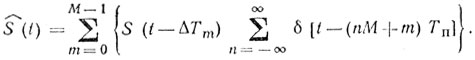(8.12)

Фурье-преобразование для (8.12) имеет вид

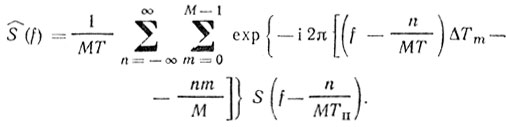(8.13)

Так как S(f) в (8.13) является преобразованием Фурье функции S(t), то

где G(⋅) - преобразование Фурье функции g(t). Так как ωT_п << 1, то член ехр (-i2πfΔT_m) изменяется медленно по сравнению с шириной G(f/ω) и справедливо приближение

ехр (-ifΔT_m) G(f/ω - υ_r) ≈ ехр (-ifυ_rΔT_m) G(f/ω - υ_r).

Это позволяет записать следующее соотношение:

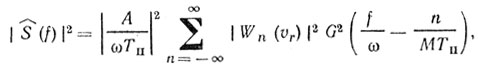(8.15)

где

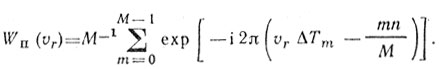
При M = 1, ΔT₀ = 0, W_n(υ_r) = 1 соотношение (8.15) определяет спектр периодической последовательности импульсов. В этом случае "слепые" скорости появляются в точках, кратных значению F_п = 1/Т_п, а однозначное определение частоты Доплера возможно только в пределах 0 - F_п/2.

При М = 2, ΔТ₀ = 0, ΔT₁ = ΔT

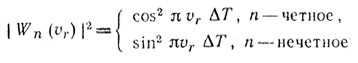
и

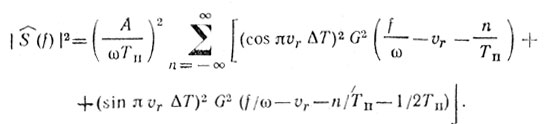(8.16)

Как следует из (8.16), спектральная картина будет повторяться с частотой 1/ΔТ, что позволяет значительно расширить диапазон однозначного измерения доплеровской частоты. Кроме того, если при постоянном периоде повторения энергия сигнала сосредоточивается в областях, кратных значению частоты повторения F_п, то при вобуляции она сосредоточивается в окрестности значений частоты, кратных 0,5F_п и F_п.

Если рассматривать пассивную помеху как сигнал, для которого υ_r = 0,

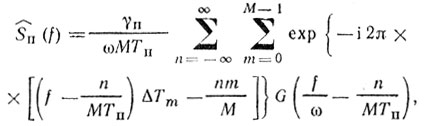(8.17)

где γ_п = S_п ехр iα; S_п - ЭПР источника пассивной помехи для анализируемого элемента дальности.

Используя приближение

можно записать

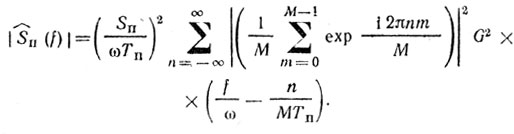(8.18)

Учитывая, что

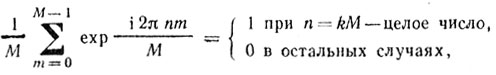
соотношение (8.19) преобразуем к виду

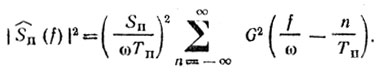(8.20)

Энергетический спектр помехи, как следует из (8.20), сосредоточивается в окрестности частот, кратных величине 1/Т_п.

При переходе в формулах (8.9), (8.11) и (8.12) от δ-функции к импульсным последовательностям с единичной амплитудой, периодом повторения T_п и длительностью τ (причем середина первого импульса совпадает с моментом времени t = 0) получаем [90]

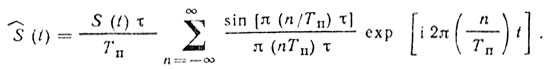(8.21)

Тогда для вобулированной последовательности импульсов с ядром вобуляции из М импульсов можно записать

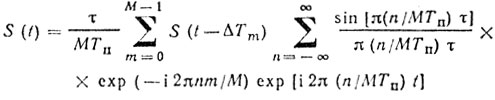(8.22)

Преобразование Фурье для (8.22) имеет вид

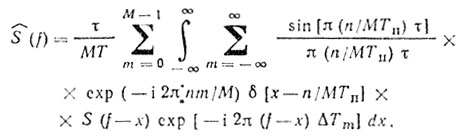(8.23)

Используя фильтрующее свойство δ-функции, получаем

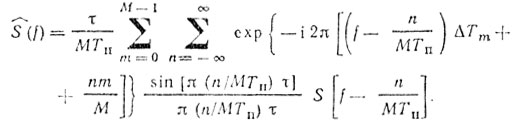(8.24)

Учитывая, что рассматривается область частот, значения которых много меньше 1/τ, имеем

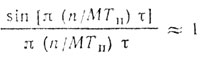
Тогда (8.24) можно привести к виду

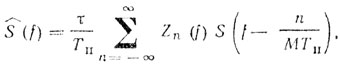(8.25)

где

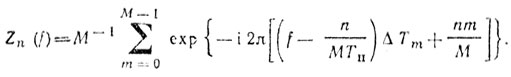(8.26)

Учитывая, что S(f) = γg(ωt) ехр (i2πF_пt) есть огибающая пачки импульсов, определяем

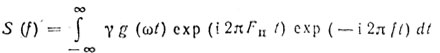(8.27)

Для большинства практически полезных случаев ДНА аппроксимируется гауссовским законом. Пусть θ_b - ширина луча ДНА при распространении в одном направлении на уровне 3 дБ, а G₀ - коэффициент усиления по мощности, тогда

где а = 1,66ω/θ_b - коэффициент, учитывающий распространение сигнала в прямом и обратном направлениях.

Подставляя (8.28) в (8.27), находим:

и

Используя соотношение 2π²/а² = 1/σ²_а, где σ²_а - дисперсия спектра помехи, возникающая из-за вращения антенны, окончательно получаем

Так как дисперсия ширины энергетического спектра пассивной помехи (см. гл. 3)

то

и уравнение (8.25) можно записать следующим образом:

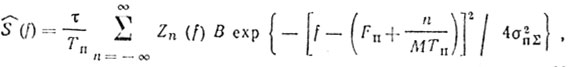(8.30)

где B = γ² G²₀/4πσ²_пΣ.

Если рассматривать частоты в окрестности значений

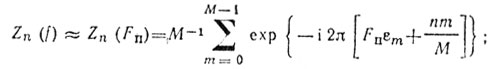(8.31)

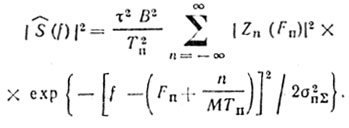(8.32)

На основании исследований спектральных свойств вобулированной последовательности импульсов в [90] получено общее выражение для расчета глубины первого нуля частотной характеристики идеализированного режекторного фильтра СДЦ:

где С₁ = |Z_n(F)|², n = рМ, р - любое целое число.

Также было найдено общее выражение для расчета коэффициента подавления помехи:

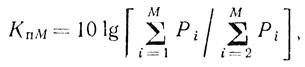(8.34)

где

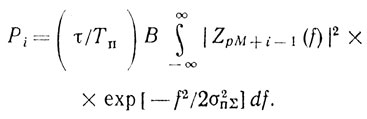
Общее решение (8.33) и (8.34) не получено, за исключением случаев М = 2 (ΔT₀ = 0; ΔT₁ = ΔT) и М = 3 (ΔT₀ = 0, ΔT₁ = ΔT, ΔT₂ = - ΔT), другими словами, для периодов следования ΔT_{п ср} - ΔT, Т_{п ср} + ΔT и Т_{п ср} - ΔT, Т_{п ср} + 2ΔT, Т_{п ср} - ΔT соответственно.

Для М = 2:

Для М = 3:

На рис. 8.6 и рис. 8.7 приведены зависимости глубины первого нуля от ΔТ/Т_{п ср} и К_п от ΔТσ_п∑.

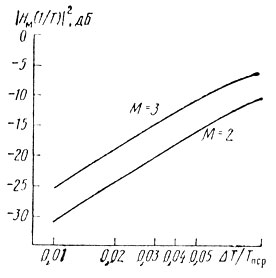
Рис. 8.6

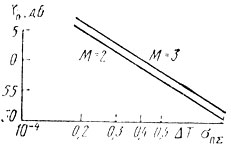
Рис. 8.7

Дальнейшие попытки получить общие выражения для расчета Н_М(1/Т_{п ср}) и К_пм, проведенные в работе [91], были связаны с представлением квадрата соотношения (8.26) в виде

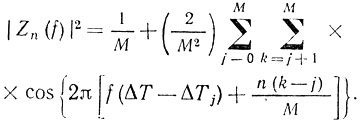(8.39)

Используя (8.39), можно показать, что глубина первого нуля определяется как

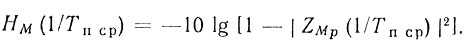(8.40)

Коэффициент улучшения (или коэффициент подавления) при условии, что коэффициент усиления режекторного фильтра равен единице:

где

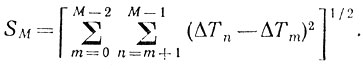(8.42)

Выражение (8.41) можно привести к более простому виду [92];

где

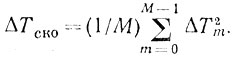
При М = 2 и М = 3 соотношение (8.43) полностью согласуется с формулами (8.36) и (8.38).

В заключение параграфа еще раз отметим, что приведенные аналитические соотношения для расчета глубины первого нуля скоростной характеристики и коэффициента улучшения были получены в предположении, что режекторный фильтр имеет идеальную характеристику и, следовательно, количественные соотношения, получаемые с помощью указанных формул, служат в качестве их верхней границы. Оценки, более близкие к реальным, можно получить с помощью статистического моделирования [92].