8.4. Спектрально-корреляционные свойства последовательности импульсов с хаотической модуляцией периода повторения

Несмотря на то что при случайном изменении длительности периода повторения провалы в окрестности бывших "слепых" скоростей получаются глубже, чем при детерминированном выборе четырех или пяти межпериодных интервалов, интерес к возможности использования такой зондирующей последовательности не ослабевает [94]. Поэтому проанализируем спектрально-корреляционные свойства последовательности импульсов с хаотической модуляцией периода повторения, что позволит в известной степени качественно оценить возможные преимущества и недостатки системы СДЦ, использую щей такой сигнал. В качестве математической модели зондирующих импульсных последовательностей с хаотической модуляцией, представляющих собой обширный класс дискретно-кодированных сигналов [11], можно принять радиоимпульсные случайные последовательности

Прежде чем приступить к исследованию спектрально-корреляционных свойств таких сигналов, рассмотрим кратко общие свойства импульсных случайных процессов и определим, к какому из них относятся зондирующие сигналы, используемые в системах СДЦ.

Следуя [34], все радиоимпульсные случайные процессы можно разделить на два класса, без накопления дисперсии модулируемого параметра и с накоплением. В свою очередь, каждый класс подразделяется на перекрывающиеся и неперекрывающиеся процессы. На примере последовательности импульсов со случайным периодом повторения рассмотрим каждый из классов.

В процессах первого класса модуляция периода повторения осуществляется относительно детерминированного среднего значения Т_п. Момент появления i-го импульса удовлетворяет условию

где ΔT_i - случайное отклонение от среднего значения.

Случайные величины t_i имеют распределение с разными средними значениями t¯_i = iТ₀, но с одинаковой дисперсией

Характерной особенностью такой случайной последовательности импульсов является то, что дисперсия σ² моментов появления различных импульсов с ростом номера i остается постоянной. Поэтому такой импульсный процесс и называют процессом без накопления дисперсии модулируемого параметра. Энергетический спектр его является дискретно-сплошным.

Для процессов второго класса момент появления i-го импульса определяется соотношением

где Т_i = t_i - t_i-1. Вследствие предполагаемой независимости случайных величин Т_i получим, что

и соответственно для дисперсии

где σ² - дисперсия случайной величины Т_i.

Характерной особенностью данной последовательности импульсов является увеличение дисперсии для момента появления импульса t_i с ростом номера. Энергетический спектр такого процесса является сплошным.

Условие неперекрытия импульсов в общем случае имеет вид

где τ_i - длительность i-го импульса.

Хорошо известно, что без селекции по частоте обеспечить достаточную помехоустойчивость по отношению к пассивным помехам практически не удается при любом законе модуляции зондирующего сигнала. Такая селекция в сочетании с разрешающей способностью по дальности возможна лишь при линейчатом спектре закона модуляции зондирующего сигнала. Наиболее распространенными сигналами такого вида являются периодические с произвольной внутрипериодной модуляцией. Другими словами, необходимо использовать в качестве зондирующего сигнала радиоимпульсный случайный процесс без накопления дисперсии модулирующего параметра.

Перейдем к определению функции неопределенности импульсного случайного процесса. Известные соотношения [11-13], позволяющие найти функцию неопределенности, справедливы только при детерминированных и дискретно-кодированных сигналах с изменением параметров по конкретно заданному коду. И тот и другой сигнал хороши только при решении какой-либо узкой задачи (например, при измерении дальности до цели или измерении доплеровской частоты) или когда существует достаточно полная априорная информация о радиолокационной обстановке, которая позволяет с помощью определенного кода создать требуемую форму функции неопределенности. Для анализа спектрально-корреляционных свойств последовательностей с хаотически изменяющимися параметрами в первую очередь необходимо определить, что мы будем понимать под функцией неопределенности импульсного случайного процесса.

Пусть ξ(t) - комплексная функция времени, описывающая поведение импульсного случайного процесса. Рассмотрим k-ю реализацию ξ^k_T(t) на интервале t₁ ≤ t ≤ t₁ + Т, где t₁ - начало отсчета; Т = NT_{п ср} - время наблюдения; N - число импульсов.

В общем виде ξ^k_T(t) определяется формулой

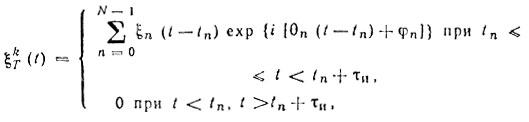
где ξ(t) - амплитудная модулирующая функция; θ(t) - фазовая модулирующая функция; φ_n - начальная фаза; t_n = nТ_{п ср} + ΔТ_n, ΔТ_n - случайное отклонение от среднего значения периода повторения.

Не записывая выражения для двумерного распределения, заметим лишь, что произведение ξ^k_T(t)ξ^k_T(t + τ) существует при одновременном выполнении двух условий [34, 38]:

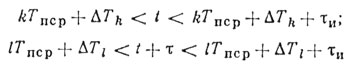
Если хотя бы одно из этих неравенств не соблюдается, то ξ^k_T(t)ξ^k_T(t + τ) = 0. Отсюда видно, что функция корреляции зависит не только от τ, но и от t, так что рассматриваемый импульсный случайный процесс является нестационарным.

Запишем функцию неопределенности для ξ^k-й реализации ξ^k_T(t):

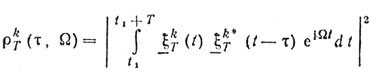
Очевидно, что функция ρ^k_T(τ, Ω) зависит не только от τ и Ω, но еще и от k и T, т. е. конкретно выбранной реализации и ее длительности. Нам же необходимо среднее значение этой функции, которое не зависело бы ни от Т, ни от номера реализации k. Усреднение по одной переменной дает функцию, зависящую от второй переменной. Таким образом, для нестационарного процесса среднее по множеству зависит от времени, а среднее по времени - от номера реализации. Для стационарного эргодического процесса среднее по времени совпадает со средним по множеству. Это значит, что оба средних, будучи равны друг другу, не зависят ни от времени, ни от реализации.

В случае нестационарного процесса для получения спектров и функций корреляции, не зависящих ни от времени, ни от реализации, необходимо выполнить усреднение дважды (т. е. как по времени, так и по множеству) порядок усреднения безразличен [37). Полученные таким образом функции следовало бы в отличие от обычных называть средним спектром, средней функцией корреляции и средней функцией неопределенности. Средний энергетический спектр и средняя корреляционная функция по-прежнему связаны между собой преобразованиями Фурье [37, 38].

Иногда при рассмотрении класса импульсных случайных процессов без накопления дисперсии модулируемого параметра говорят об их стационарности и эргодичности. Под этим обычно понимают, что указанную группу случайных процессов можно представить в форме периодической последовательности радиоимпульсов, параметры которой модулированы случайной стационарной эргодической модулирующей функцией с дискретным временем. Иначе говоря, указанные импульсные процессы представляют собой результат наложения стационарной эргодической случайной последовательности параметров импульсов на детерминированную последовательность тактовых импульсов. Только с учетом этого замечания можно говорить об эргодичности и о стационарности рассматриваемого импульсного случайного процесса.

Требование эргодичности здесь необходимо по следующей причине. Хотя для стационарного, но не эргодического процесса предел функции

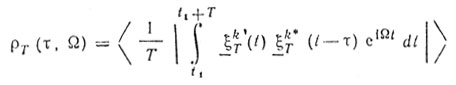(8.44)

существует, нельзя утверждать, что случайная функция ρ_Т(τ, Ω) при Т → ∞ сходится к предельному значению ρ(τ, Ω) (оператор <> означает усреднение по ансамблю реализации). Можно показать, что дисперсия ρ_Т(τ, Ω) [37, 38] при Т → ∞ остается конечной, т. е. этот предел при любых значениях τ и Ω является случайной величиной и не может сходиться к ρ(τ, Ω). При стационарном и эргодическом процессах при → ∞ функция ρ_Т(τ, Ω) сходится к предельному значению ρ(τ, Ω) равномерно относительно момента t₁: -∞ < t₁ < ∞ [37, 38].

Найдем функцию неопределенности импульсного случайного процесса. С учетом вышесказанного

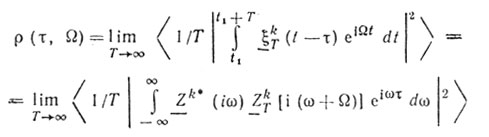
будем считать функцией неопределенности импульсного случайного процесса.

Нормированная функция неопределенности при условии, что все импульсы последовательности одинаковые, записывается так:

где ρ_и(0, 0) - функция неопределенности одиночного импульса.

Когда время наблюдения ограничено интервалом Т, нормированная функция неопределенности

где ρ(τ, Ω) определяется выражением (8.44).

С учетом (8.44)

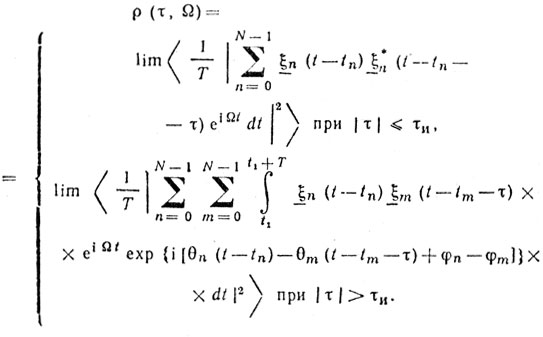(8.46)

Найдем теперь функцию неопределенности последовательности импульсов с хаотическим периодом повторения. Комплексная модулирующая функция последовательности радиоимпульсов с хаотической модуляцией периода повторения записывается следующим образом

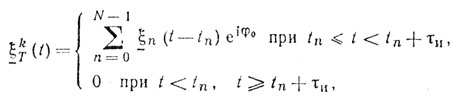
где φ₀ - начальная фаза, одинаковая для всех импульсов; t_n = nТ₀ + ΔT_n - момент появления n-го импульса. Плотность вероятности W(ΔТ_n) известна; |ΔТ_n| ≤ γТ₀; γ - коэффициент вобуляции, выбираемый из условия непересечения импульсов γ < 0,5[1 - τ_и/T_{п ср}].

Как было показано выше, для нахождения функции неопределенности необходимо вычислить соотношения типа:

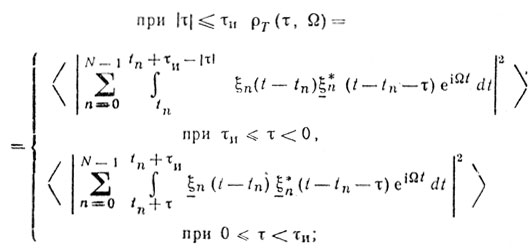
при |τ| > τ_и

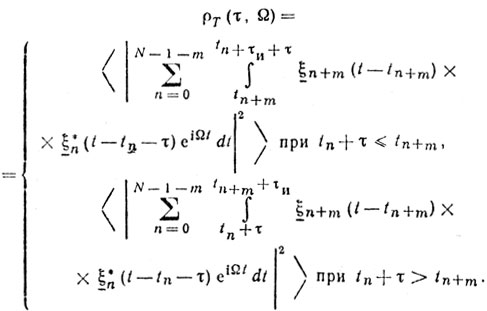
В [39] показано, что при |τ| ≤ τ_и

где

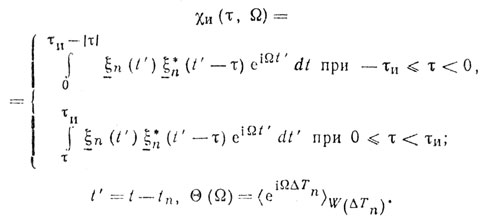
Учитывая, что ρ_Т(0, 0) = N²|χ_и(0, 0)|², получаем

При |τ| > τ_и

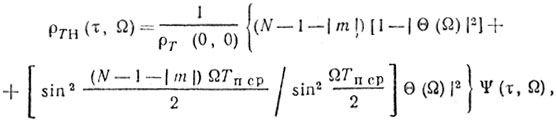
где τ = mT + τ'; m = ±1; ±2; ...; ±(N - 1); |τ'| ≤ 2γT_{п ср} + τ_и;

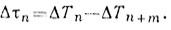
Плотность вероятности W (Δτ_n) при условии статистической независимости случайных величин ΔТ_n и ΔТ_n+m определяется по хорошо известной формуле [34]

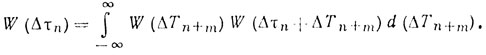
При статистическом усреднении по Δτ_n, следуя работе [34], можно выделить четыре области интегрирования, которые зависят от области значений τ' [39].

Если рассматривать значения -2γТ - τ_и ≤ τ' ≤ 0, то имеем:

Первая область -2γТ_{п ср} - τ_и ≤ Δτ_n < -2γТ_{п ср}: при τ' + Δτ ≤ 0 |τ'| - τ_и ≤ Δτ_n -2γТ_{п ср}; при τ' + Δτ_n > 0 значений Δτ_n, удовлетворяющих этому неравенству, не существует.

Вторая область -2γT_{п ср} ≤ τ' < - 2γT_{п ср} + τ_и:

при τ' + Δτ_n ≤ 0 |τ'| - τ_и ≤ Δτ_n < |τ'|;

при τ' + Δτ_n > 0 |τ'| ≤ Δτ_n < 2γТ_{п ср}.

Третья область - 2γT_{п ср} + τ_и ≤ τ' < -τ_и.

при τ' + Δτ_n ≤ 0 |τ'| - τ_и ≤ Δτ_n < |τ'|,

при τ' + Δτ_n > 0 |τ'| ≤ Δτ_n < |τ'| + τ_и.

Четвертая область -τ_и ≤ τ' < 0:

при τ' + Δτ_n ≤ 0 |τ'| ≤ Δτ_n < |τ'|;

при τ' + Δτ_n > 0 |τ'| ≤ Δτ_n < |τ'| + τ_и.

Аналогично определяются пределы интегрирования для 0 ≤ τ' ≤ 2γТ_{п ср} + τ_и. При условии четности функции W(Δτ_n), т. е. четности W(ΔT_n) и W(ΔT_n+m), функция Ψ(τ', Ω) также обладает свойством четности по переменной τ' относительно среднего значения периода повторения Т_п. В этом случае нет необходимости в вычислении функции Ψ(τ', Ω) для значений 0 < τ' ≤ 2γT_{п ср} + τ_и. Если же W(Δτ_n) нечетная, необходимо найти функцию Ψ(τ', Ω) для восьми областей интегрирования.

Перейдем к анализу основных сечений функций неопределенности последовательности когерентных импульсов с хаотической модуляцией периода повторения.

При τ = 0 имеем

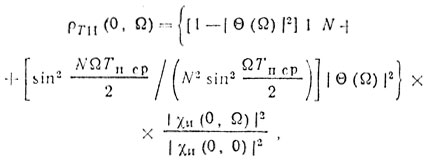(8.47)

при N → ∞ соотношение (8.47) принимает вид

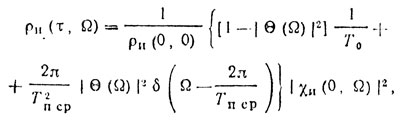(8.48)

где r - целое число.

Если предположить, что импульсы имеют прямоугольную форму и единичную амплитуду, то последняя формула совпадает с хорошо известным соотношением, которое определяет энергетический спектр последовательности прямоугольных импульсов с хаотической модуляцией [36].

Рассмотрим отдельно непрерывную и дискретную составляющие функции неопределенности, которые характеризуются соответственно первым и вторым слагаемыми в (8.47) и (8.48).

Дискретная составляющая напоминает энергетический спектр равномерной последовательности импульсов с промодулированными характеристической функцией амплитудными значениями. Непрерывная составляющая представляет собой как бы шумовой фон. При этом в окрестности Ω = 0 влияние непрерывной составляющей практически не сказывается. Увеличивая коэффициент вобуляции, можно значительно снизить амплитуды максимумов дискретной составляющей. Ценой за "разрушение" периодической структуры будет рост непрерывной составляющей, которая, попав в полосу пропускания режекторного фильтра, снизит эффективность его работы.

При сечении функции неопределенности плоскостью Ω = 0 необходимо рассматривать два случая: |τ| ≤ τ_и и |τ| > τ_и.

При |τ| ≤ τ_и

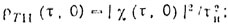
и в случае прямоугольных импульсов

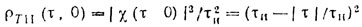
При τ > τ_и

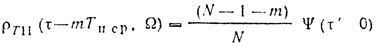
Таким образом, при разработке рекомендаций по выбору закона модуляции и параметров модулирующего сигнала необходимо исследовать

поведение дискретной составляющей функции неопределенности.

соотношение между дискретной и непрерывной составляющими для различных значений скважности и глубины вобуляции;

влияние условия, однозначного определения дальности на допустимую глубину вобуляции.

Качественный анализ спектрально-корреляционных свойств последовательности импульсов с хаотической модуляцией позволяет сделать вывод о том, что повышение эффективности РЛС в окрестности бывших "слепых" скоростей будет сопровождаться снижением эффективности в окрестности бывших "оптимальных" скоростей цели за счет возникновения непрерывной составляющей, которая должна рассматриваться как помеховый сигнал, поступающий в полосу прозрачности режекторного фильтра. Возможным путем повышения эффективности в окрестности бывших "оптимальных" скоростей является использование совместно с вобуляцией периода повторения нескольких несущих частот, что, кроме того, позволит повысить помехоустойчивость РЛС по отношению к активным помехам.