Глава 9. Требования к узлам РЛС СДЦ

9.1. Влияние нестабильности работы узлов РЛС на эффективность систем обработки сигналов

Проблема оценки эффективности РЛС СДЦ состоит из нескольких самостоятельных, но связанных между собой задач выбора критериев эффективности, выявления факторов, снижающих или ограничивающих эффективность и учет влияния этих факторов; выработки требований на допустимую величину каждого фактора, снижающего эффективность; разработки методов и аппаратуры для измерения величины каждого ограничивающего фактора.

Синтез систем обработки сигналов в РЛС проводится для оптимизации задач обнаружения и оценки параметров применительно к определенным тактическим ситуациям, кинематическим характеристикам цели и набору помех, состоящему из собственных шумов приемного тракта и пассивных помех. Однако, как правило, при таком синтезе не учитываются помехи, возникающие из-за нестабильной работы узлов системы обработки сигналов. Это объясняется тем, что пока неясна техническая реализация системы обработки сигналов, трудно выяснить источники таких помех. Поэтому на этапе технического проектирования системы вырабатываются требования на нестабильность работы узлов обработки. При этом действие таких помех минимизируется до заданного допустимого уровня. Но вместе с тем даже малый уровень помех из-за нестабильностей, добавляясь к основному уровню пассивных помех и шумов, снижает надежность обнаружения. Увеличивается F - вероятность ложных тревог, уменьшается D - вероятность правильного обнаружения и, следовательно, повышается пороговая мощность Р_пор. Чтобы компенсировать это снижение надежности уже на этапе синтеза следует предусмотреть допуски на D и F или на P_пор. Кроме того, следует проанализировать источники нестабильностей в целом как нестабильность алгоритма обработки сигналов и локализовать источники возникновения помех в их взаимной связи. В общем случае:

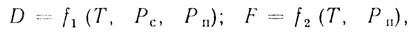
где Т - порог решения по определенному критерию.

Тогда в первом приближении:

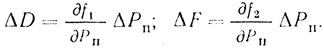
Следовательно, нужно задавать допуски ΔD и ΔF. Если считать, что ΔР - случайная величина, то, очевидно, что

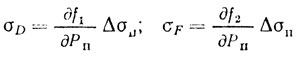
и поэтому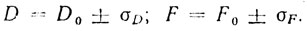

Для эффективной работы необходимо ввести допуски:

Отсюда можно найти

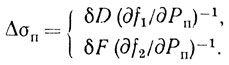(9.2)

Логично использовать относительное непостоянство σ_п, введением коэффициента модуляции

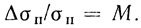(9.3)

Что касается детерминированных нестабильностей, причиной которых могут быть наводки, пульсации, вибрации и ускорения, то целесообразно их учитывать также коэффициентом модуляции, определяемым как

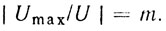(9.4)

Следует иметь в виду, что коэффициенты m и М всегда малы. В самом деле, при коэффициенте подавления в системе обработки сигналов, большем 10 дБ, аппаратурные нестабильности должны быть снижены до еще меньшего уровня. Поэтому при расчете нестабильностей можно учитывать эффекты только первого порядка малости, отбрасывая эффекты высших порядков.

Если представить радиолокационную систему обработки сигналов укрупненно в виде последовательно включенных системы внутрипериодной обработки сигналов (СВО), си стемы межпериодной обработки сигналов (СМО) и порогового устройства (ПУ) (рис. 9.1), то, вводя алгоритмические операторы F обработки

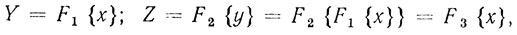
получаем

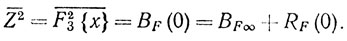(9.5)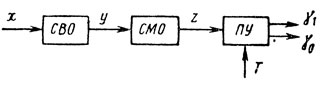

Рис. 9.1

По очевидным соображениям после системы межпериодной обработки B_F∞ = 0, следовательно, Z¯² = R_F(0).

Величина Z¯² является некоторой функцией, зависящей от алгоритма обработки сигналов, корреляционной функции суммы пассивных помех и внутренних шумов, а также корреляционной функции помех из-за нестабильностей алгоритма обработки. Следует отметить, что система межпериодной обработки может как подавлять, так и подчеркивать помехи из-за нестабильности алгоритма обработки сигналов в зависимости от вида корреляционной функции этих помех. Таким образом, точное выражение

можно получить в замкнутой форме, только зная алгоритм обработки сигналов в конкретной радиолокационной системе.

Возможен и иной подход к решению этой проблемы. Он заключается в приведении всех помех ко входу системы межпериодной обработки, определению величины R_у(τ) = (y(t) y(t - τ))¯ и нахождению алгоритма преобразования корреляционной функции системой межпериодной обработки:

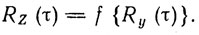
Если после этого удается разделить R_z(τ) на две составляющие:

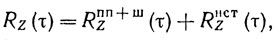
где R^пп+шz(τ) - корреляционная функция пассивных помех и шума; R^нст_z(τ) - корреляционная функция погрешностей из-за нестабильности алгоритма, то Δσfп ≡ R^нст_z(0).

Возвращаясь к помехам из-за нестабильностей алгоритма, заключаем, что его можно представить как некоторую функцию последовательности операций над входными реализациями (преобразования, усиления, детектирования и т. п.). Тогда, учитывая малость фактора нестабильности, можно в первом приближении для разделения влияния отдельных операций использовать формулу полного дифференциала [1, 41]. В самом деле, если

где α₁, ..., α_n, - параметры операции; х - входные реализации, то

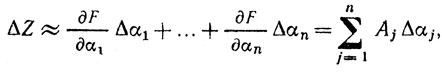
где A_j = ∂F/∂α_j - парциальный весовой коэффициент, определяемый численным значением частной производной.

Корреляционная функция в предположении независимости и некоррелированности операций будет

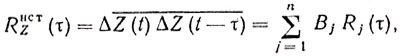
где B_j = A²_j - парциальный весовой коэффициент операции.

Считая, что R^пп+шz(τ) - BR₀(τ), получаем

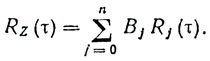(9.6)

Определив G_j(f) или R_j(τ), можно найти суммарную корреляционную функцию или суммарный энергетический спектр. Вид выражений R_j(τ) зависит от характера нестабильностей операций или узлов обработки, который может быть случайным или детерминированным. Кроме того, все нестабильности могут быть разделены на амплитудные, фазовые и временные. Интервал, на котором должны быть определены корреляционные функции, задается временем обработки.

Рассмотрим фазовые нестабильности с точки зрения их связи с построением РЛС и влияния на них различных узлов, участвующих в обработке входных реализаций. При этом будем считать, что разность фаз принимаемого и опорного сигналов выделяется таким элементом, как фазовый или когерентный детектор. Следует отметить, что в формировании этой разности фаз φ_р(t) при различных вариантах построения РЛС участвуют различные узлы. Например, для РЛС, показанной на рис. 9.2, фазирование (фазовая синхронизация) осуществляется от генератора радиочастоты на промежуточной частоте, сравнение колебаний также происходит на промежуточной частоте. Когерентный гетеродин, как правило, работает в прерывистом режиме для облегчения условий фазирования. Как видно, разность фаз сигнала помехи и опорного сигнала когерентного гетеродина равна в момент сравнения [1]

где φ'₂(t) = φ₂(t) - φ_г(t) - фаза отраженного сигнала помехи на промежуточной частоте; φ₂(t) - фаза отраженного сигнала помехи на радиочастоте; φ_г(t) - фаза сигнала гетеродина; φ'_кг(t) - фаза опорного сигнала когерентного гетеродина, работающего на промежуточной частоте.

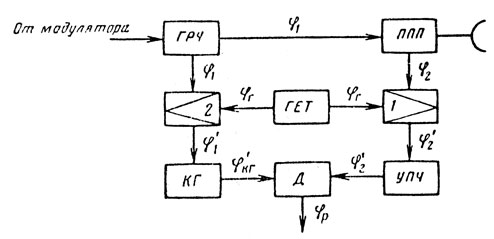
Рис. 9.2

Подставляя в выражение (9.7) соотношение для φ'₂ и φ'_кг, получаем

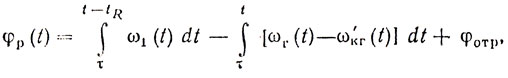
а в момент прихода сигнала при t = t_R

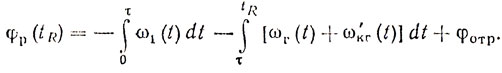(9.8)

При перемене направления фазовой синхронизации в рассмотренной системе приходим к построению, показанному на рис. 9.3, где изображена истинно когерентная система, полученная заменой генератора радиочастоты усилителем мощности. Для системы, изображенной на рис. 9.3, используя принятые обозначения, получаем

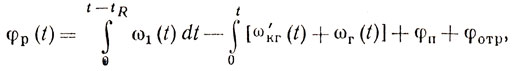
а при t = t_R

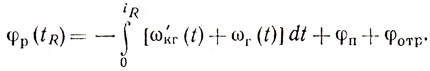(9.9)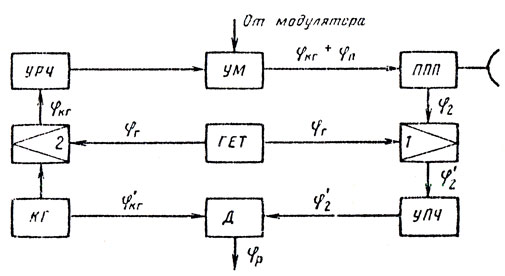

Рис. 9.3

Следовательно, постоянство φ_р зависит от стабильности и частоты колебаний когерентного гетеродина и гетеродина и от постоянства набега фазы в тракте пере датчика Δφ_п.

На рис. 9.4 представлено построение РЛС с фазированием на радиочастоте от генератора радиочастоты и со сравнением сигналов на радиочастоте.

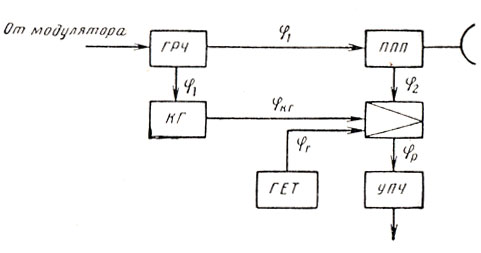
Рис. 9.4

Для такого построения

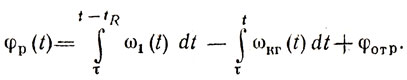
Полагая t = t_R, получаем

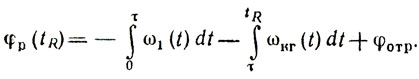(9.10)

Постоянство φ_р определяется стабильностью частоты колебаний генератора радиочастоты и когерентного гетеродина. При изменении направления фазирования (рис. 9.5) получаем соотношение

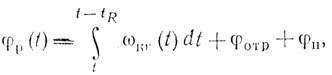(9.11)

что при t = tR даст φр(tR) = -∫tR0ωкг(t)dt + φотр + φп. Значит, постоянство φр зависит только от стабильности частоты колебаний когерентного генератора и набега фазы в передающем канале.

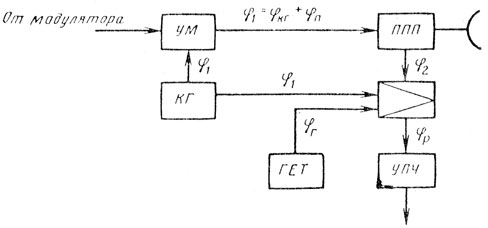
Рис. 9.5

При фазировании от генератора радиочастоты на радиочастоте сравнение отраженных сигналов с опорным напряжением может производиться на промежуточной частоте, как показано на рис. 9.6. В этом случае

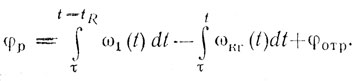(9.12)

При t = t_R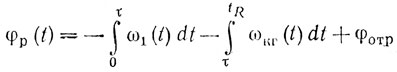

и, следовательно, постоянство φ_р зависит от стабильности частоты колебаний генератора радиочастоты и когерентного гетеродина.

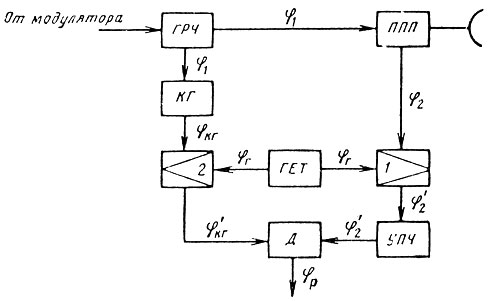
Рис. 9.6

При изменении направления фазовой синхронизации, как это показано, на рис. 9.7, получаем соотношение

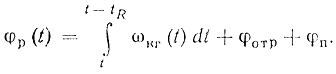(9.13)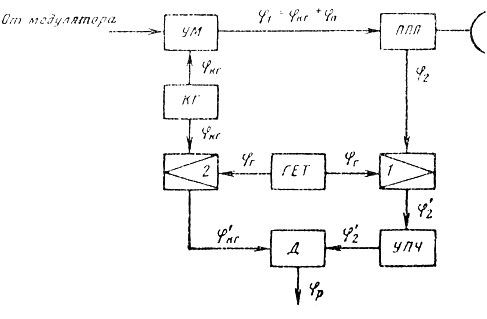

Рис. 9.7

Полагая t = t_R,

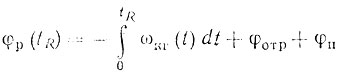
и постоянство φ_р будет определяться стабильностью опорного колебания когерентного гетеродина и набега фазы в тракте передатчика. РЛС можно выполнить по схеме, в которой фазирование от генератора радиочастоты производится на промежуточной частоте, а сравнение опорного колебания с отраженными сигналами осуществляется на радиочастоте. Такое построение РЛС показано на рис. 9.8. В этом случае

(9.14)

и при t = t_R

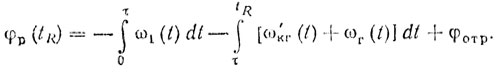
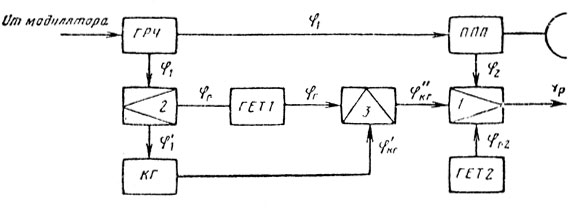
Рис. 9.8

Постоянство φ_р определяется стабильностью частоты колебаний генератора радиочастоты, гетеродина ГЕТ1 и когерентного гетеродина. Если направление фазовой синхронизации изменить, то согласно рис. 9.9 получаем

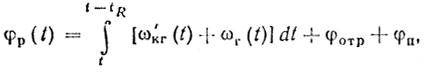(9.15)

что при подстановке t = t_R дает

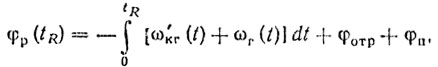
и, следовательно, постоянство φ_р может быть обеспечено за счет стабильности частоты колебаний гетеродина ГЕТ1, когерентного гетеродина и постоянства набега фазы в передатчике. При использовании в передатчике усилителей мощности, особенно таких, как лампа бегущей волны, платинотрон и усилительный клистрон, набеги фазы могут достигать больших значений. Для их ликвидации применяют схему построения, показанную на рис. 9.10. При таком построении системы фазирования и сравнения

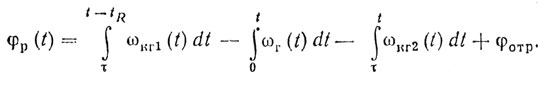(9.16)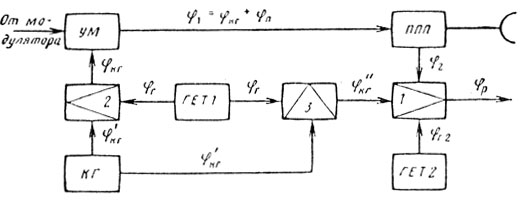

Рис. 9.9

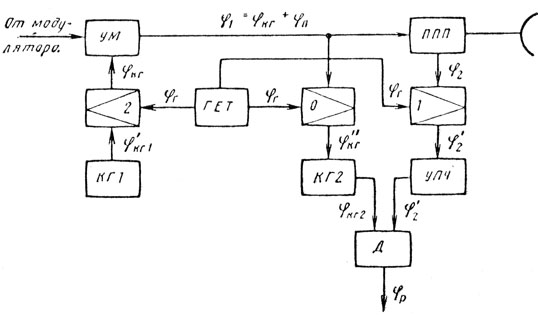
Рис. 9.10

При t = t_R получаем

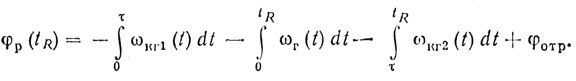(9.17)

Таким образом, видно, что постоянство φ_р зависит от стабильности частоты колебаний когерентных гетеродинов КГ1 и КГ2 и ГЕТ, но не зависит от фазового набега в канале передатчика φ_п. Анализируя приведенные схемы построения, можно сделать заключение, что в тех случаях, когда фазовая синхронизация производится от когерентного гетеродина, РЛС по существу перестает быть псевдокогерентной и становится истинно когерентной.

При фазовой синхронизации когерентного гетеродина от генератора радиочастоты начальная фаза фазирующего импульса случайна и распределена в пределах ±π. Фазовая синхронизация в этом случае должна осуществляться в каждом периоде на отрезке времени, не превышающем длительности зондирующего импульса при изменяющихся в широких пределах начальных условиях.

Качество преобразования разности фаз φ_р и влияние элемента сравнения (фазового детектора) на обработку входных реализаций можно учесть, рассматривая фазовый детектор как перемножитель. Принимая во внимание соотношения (9.8)-(9.16), полученные выше, можно сделать заключение, что непостоянство или нестабильность алгоритма межпериодной обработки будет зависеть от таких факторов, как фазовые и амплитудные нестабильности генератора радиочастоты, местного и когерентного гетеродина и приемного тракта (УВЧ, УПЧ), временные нестабильности модулятора и системы "хронизатор - система подавления". Все эти нестабильности можно исследовать по от дельности из-за их малости и возможности учета только в первом приближении.

Что касается фазовых нестабильностей, то их влияние будет зависеть от характера фазовых уходов, а также времени и структуры обработки сигналов.

Задавая характеристику элемента сравнения (фазового детектора) в виде U = α cos φ_р, получаем

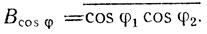
Считая φ распределенным равновероятно в пределах ±π и используя первое приближение, находим

Очевидно, что

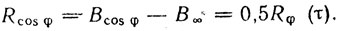
Если характер ухода фазы и частоты случайный и справедливо предположение о нормальности закона распределения вероятностей отклонения от среднего значения [42, 44], то, следуя [43, 44], получаем

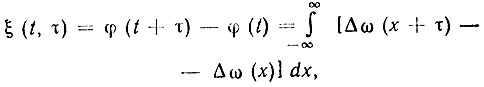
тогда

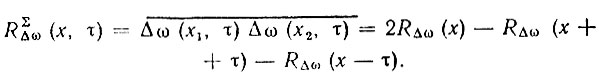
Согласно теореме Винера - Хинчина

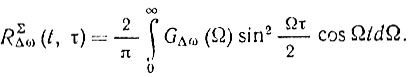
Считая Δω(t) стационарным случайным процессом, используем теорему об интегрировании стационарного процесса [45] и получаем

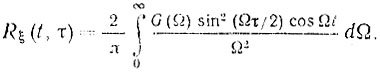(9.17)

Если в (9.17) положить t = 0, то

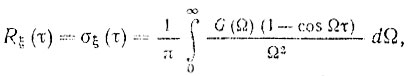(9.18)

что полностью совпадает с результатом работы [44]. Следует отметить, что в (9.17), (9.18) G(Ω) - энергетический спектр флуктуации частоты колебаний.

Амплитудные нестабильности также характеризуются корреляционными функциями вида:

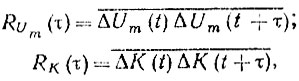(9.19)

где U_m - амплитуда сигнала генератора или гетеродина; К - коэффициент усиления тракта.

То же относится и к характеристикам временных нестабильностей

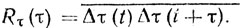(9.20)

Таким образом, имеется совокупность характеристик флуктуации операций алгоритма обработки и набор возможных алгоритмов работы радиолокационной системы, позволяющих определить результирующее изменение мощности помех и, следовательно, изменение вероятностей правильного обнаружения и ложной тревоги [41, 44].