9.2. Требования к стабильности работы узлов когерентно-импульсной РЛС

Обычно учет нестабильностей операций алгоритма обработки сигналов или узлов РЛС проводится для определения допустимой нестабильности каждого отдельного узла. В этой связи приходится иметь дело с задачами двух видов: формирование требования к стабильности отдельного узла; распределение требования к стабильности всей совокупности узлов.

Рассмотрим первую задачу. Имея в виду фазовые нестабильности и учитывая наличие фазочувствительного элемента сравнения, будем вначале учитывать только регулярные нестабильности частоты или фазы. Такой подход широко применяется в радиолокации. Используя один из возможных алгоритмов, описанных в § 9.1, и рассматривая в качестве блока межпериодной обработки однократную систему ЧПК, определяем разность фаз за время обработки (Т_п) как

На малых отрезках времени τ = Т_п можно с достаточной степенью точности аппроксимировать уход частоты генератора [1, 42] линейным законом:

с параметром α = dω/dt, являющимся постоянным в каждой отдельной реализации (в пределах Т_п). Тогда

или же можно считать, что от периода к периоду повторения имеется уход частоты Δω = αT_п, появляющийся как начальная расстройка, отнесенная к началу периода повторения. В этом случае

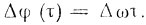(9.22)

Корреляционные функции этих величин:

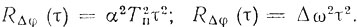
Следующим шагом является учет того обстоятельства, что уходы частоты и фазы носят случайный характер. Исследования [42] показали, что уходы частоты генераторов на малых интервалах времени под воздействием всей совокупности дестабилизирующих факторов, таких, как тепловые и дробовые шумы, флуктуации электронного потока, пульсация источников питания и вибрации, могут быть удовлетворительно аппроксимированы на отрезках времени, меньших секунды, линейным законом с параметром α, распределенным по нормальному закону:

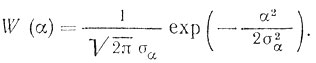
Следовательно, усредняя квадраты ухода частоты и фазы, получаем:

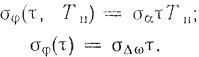(9.23)-(9.24)

Таким образом, при любом варианте построения радиолокационного тракта для каждого его узла определены требования на фазовую и частотную стабильности (табл. 9.1 и 9.2). В ряде случаев не удается удовлетворительно аппроксимировать закон ухода частоты линейной зависимостью. При воздействии вибраций, акустических полей, пульсаций источников питания и магнитных наводок полезной оказывается аппроксимация уходов частоты гармоническим законом:

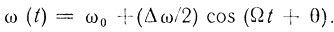
Таблица 9.1

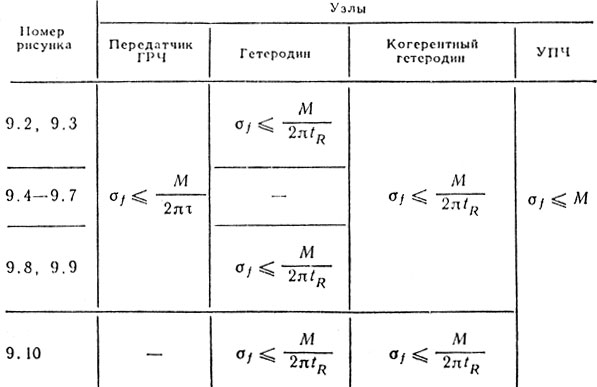
Таблица 9.2

Здесь следует учесть взаимную фазировку (0) обрабатываемых сигналов с периодом T_п и дестабилизирующего фактора с частотой F = Ω/(2π). При ЧПВ, усредняя отклонения фазы за период повторения по всем возможным значениям случайной начальной фазы θ, получаем

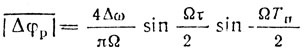
При малых Ωτ(Ωτ < π/6) и F = 2n-1/2 F_п

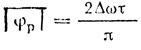
или, вводя индекс частотной модуляции m_Ω = Δω/2Ω, получаем

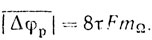(9.25)

В табл. 9.3 приведены требования на стабильность частоты узлов различных радиолокационных трактов при гармонической аппроксимации законов ухода частоты.

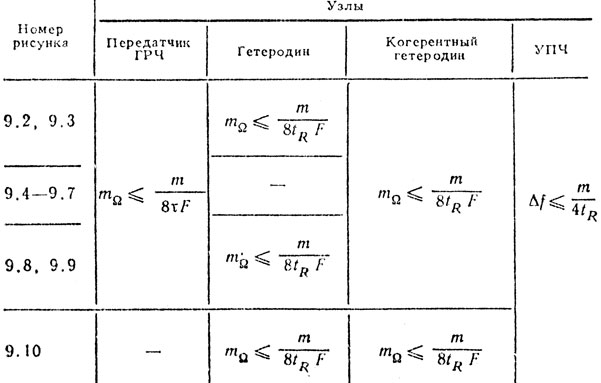
Таблица 9.3

Что касается амплитудных нестабильностей алгоритма обработки сигнала, то они обычно оказывают меньшее влияние на эффективность обработки. При тех же допущениях и ограничениях, что и выше, сформулируем следующие требования. Для амплитуд генераторов (радиочастоты, местного гетеродина, когерентного гетеродина и т. д.) относи тельное постоянство амплитуды должно быть меньше М:

Для коэффициента усиления тракта обработки относи тельное постоянство коэффициента усиления должно быть меньше М:

Временные нестабильности возникают по нескольким причинам. Во-первых, из-за нестабильности длительности импульсов модулирующих передатчик. В этом случае ставятся очевидные требования

Во-вторых, из-за рассогласования периода повторения импульсов и времени задержки их в системе подавления. Тогда [1]

где Δ = τ_з - Т_п.

Следует отметить, что последнее обстоятельство проявляется лишь в динамических системах подавления пассивных помех.

Требования на стабильность, о которых говорилось выше, относятся к системам межпериодной обработки простейшего вида - однократным системам ЧПК. При использовании обработки с большей кратностью вычитания детерминированные уходы частоты генераторов перестают увеличивать мощность помех на выходе системы обработки сигналов. При случайном характере уходов частоты, некоррелированных от периода к периоду повторения, и аппроксимации закона ухода линейной зависимостью с постоянной скоростью ухода в пределах одного периода, т. е.

где α_j = (dω/dt)_j - скорость ухода частоты в j-м периоде повторения; α¯_kα_k = 0; α¯²_j = σ²_α, можно получить следующую зависимость результирующего приращения разностной фазы:

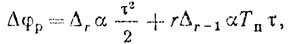
где Δ_kα - k-я разность величины α_j.

Отсюда

Поскольку σ_Δr и σ_Δr-1 выражаются через σ_α можно обо значить:

Подставляя эти выражения в (9.30), получаем

где N = n²₁τ⁴/4 + n²₂r²T_пτ²)^1/2.

Причем числовой коэффициент N > 1 и зависит в основном от r. Следовательно, используя табл. 9.1 и 9.2, при проектировании многократных систем ЧПК следует все соотношения в указанных таблицах уменьшать в N раз, т. е. повысить требования к стабильности узлов. Поскольку величины α_j некоррелированы между собой, то n₁ и n₂ определить просто. В самом деле,

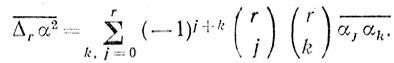
Так как α¯_jα¯_k = 0 при j ≠ k, то

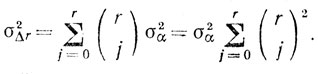
Поэтому:

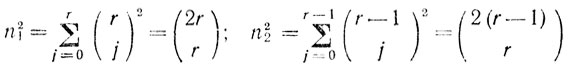(9.32)

и, наконец,

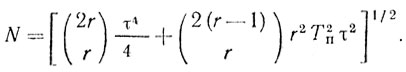(9.33)

Повторяя весь ход рассуждений и проделывая аналогичные выкладки для случая аппроксимации уходов частоты гармоническим законом, находим

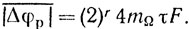(9.34)

Таким образом, для многократных систем ЧПК при гармонической аппроксимации частотных уходов требования на допустимую нестабильность узлов, приведенные в табл. 9.3, следует повысить в N раз, где N = 2^r. Рассмотрим вторую задачу [1, 46]. При анализе требований j-го узла мы исходили из соотношений:

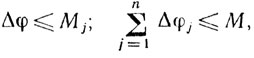(9.35)

где n - число узлов РЛС.

Из этих выражений видно, насколько важно правильно определить M_j для каждого узла РЛС. Для упрощения расчета введем так называемые парциальные коэффициенты α_j, причем

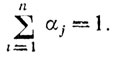
Нахождение α_j возможно с различных позиций или точек зрения.

1. Если учесть жесткость требований к каждому узлу, то требования находятся в виде допустимых эквивалентных скоростей ухода частоты (^dω/_dt)_jэ в каждом узле в предположении m_j = m. Найдя (^dω/_dt)_jэ, следует определить α_j, из соотношений:

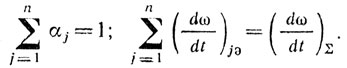
При этом:

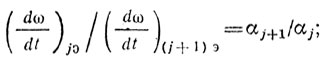
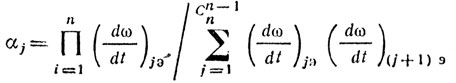(9.36)

2. Если учесть реально достижимую стабильность каждого узла в виде реальной скорости ухода частоты (dω/dt)_jp, то в предположении выполнения соотношений:

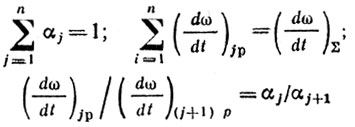
получаем

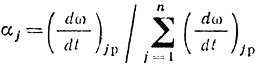
3. Наконец, предполагая независимость и равноправность узлов при случайном характере уходов частоты, можно считать

M_j = Mn^-0,5. (9.38)

Таким образом, исходя из назначения РЛС, можно выбрать схему ее построения и метод обработки сигналов, затем определить характеристику передачи всего тракта обработки и найти источники нестабильности алгоритма обработки. По характеристикам обнаружения необходимо определить величины δ и Δ. Зная δ и Δ, следует потребовать малости суммарного коэффициента паразитной модуляции за счет нестабильности работы узлов РЛС и найти его численное значение. После этого можно распределить требования и стабильности работы узлов, назначая коэффициенты α_j. Следовательно, производится своеобразная оптимизация эффективности работы узлов РЛС, что, естественно, увеличивает надежность аппаратуры.