
9.3. Анализ влияния нестабильности работы на эффективность систем подавления пассивных помех
Фактором, существенно влияющим на эффективность обработки информации, является нестабильность времени задержки в накопителе. Методом, изложенным в [47], легко найти требование к стабильности времени задержки накопителя:
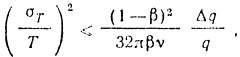
где β - коэффициент передачи кольца рециркулятора; ν - коэффициент, учитывающий форму импульсов; Δq/q - относительное допустимое уменьшение отношения сигнал-помеха.
При работе накопителя на несущей частоте, т. е. при накоплении радиоимпульсов с учетом нестабильности времени задержки кольца рециркулятора, приводящей к случайным отклонениям начальной фазы ψ накапливаемых радиоимпульсов, в предположении некоррелированности этой фазы в соседних периодах накопления методом, изложенным в [47], можно получить соотношение
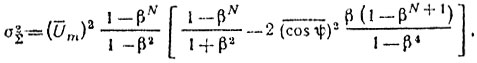 (9.39)
(9.39)где σ2∑ - дисперсия амплитуды накопленного процесса; U¯m - среднее значение амплитуды накапливаемых радиоимпульсов; cos¯ψ - среднее значение косинуса случайной начальной фазы; β - коэффициент обратной связи рециркулятора; N - число накопленных импульсов.
Среднее значение косинуса случайной начальной фазы зависит от конкретной модели закона распределения случайной фазы. Так при равномерной плотности распределения вероятностей фазы в пределах ψmax - ψmin имеем [44, 45, 47]
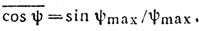
а при нормальном законе распределения вероятностей легко получить
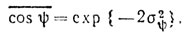
При изложенном выше анализе не принимается во внимание накопление самой фазы радиоимпульсного процесса. Если считать, что
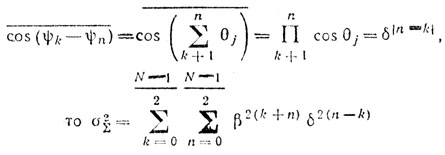
где θj - случайное изменение фазы за период повторения импульсов из-за нестабильности задержки; δ = cos θj; ψk,n - фаза им пульсов в n, к периодах повторения.
Отсюда
σ2∑ = (U¯m)2 {1-β2N/1-β4 + δβ/(1-δ2β2) × [1-β2N-2/1-β4 - δN-2βN-2(1-δβ)N-1/1+δ2β2]}
Очевидно, требование к стабильности времени задержки в этом случае формируется следующим образом.
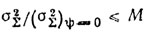 (9.40)
(9.40)Отсюда по известным N, β можно определить δ. Величина δ связана с θ¯ или θ¯2 и, следовательно, с Δτ¯з или σ2φз.
Влияние нестабильности параметров приемопередающего трак та РЛС можно оценить по уменьшению коэффициента улучшения Ку [93] путем введения амплитудной αk и фазовой θk ошибок нормированной импульсной характеристики системы обработки
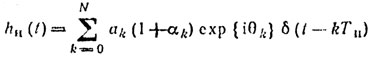
Ошибки αk и θk можно предполагать распределенными по нормаль ному закону с нулевым средним и дисперсиями σ2А и σ2θ и статистически независимыми:
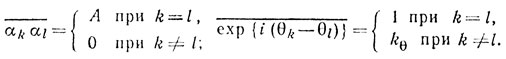
При этом:
А = σ2А; Кθ = ехр(-σ2θ) ≈ 1 - σ2θ.
Если задать энергетический спектр помехи на входе
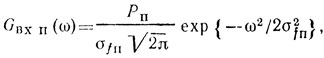
то нормированная частотная характеристика системы обработки сигнала будет
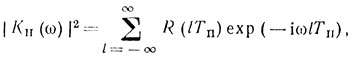
где R(lТп) = (h(mTп + lTп)h* (mTп))¯ - автокорреляционная функция импульсной характеристики системы с учетом нестабильности ее параметров.
Величину Кн(ω) можно выразить через К(ω), Kθ и А:
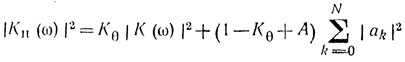
или для σ2θ << 1
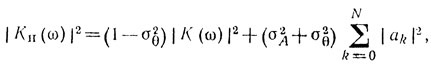
где К(ω) - коэффициент передачи идеальной системы, а N - кратность вычитания в системе обработки.
При σfп << Fп можно в интервале одного дискрета Fп, т. е. mFп - Fп/2 ≤ f ≤ mFп + Fп/2, представить энергетический спектр помехи на входе в виде
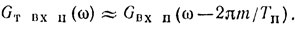
Тогда на выходе системы обработки
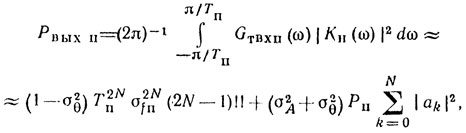
где (2N - 1)!! = 1⋅3⋅5 .. (2N - 1).
Усредненное по возможным скоростям цели значение мощности сигнала на выходе системы обработки
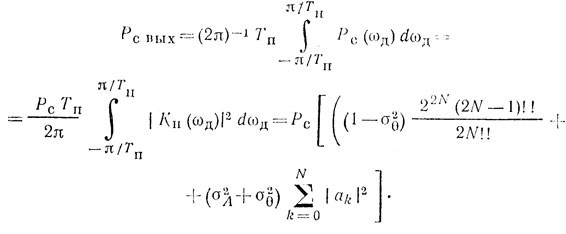
Для N-кратных систем ЧПВ 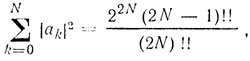 и поэтому коэффициент улучшения
и поэтому коэффициент улучшения
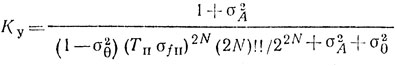

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
