10.3. Влияние отражений от подстилающей поверхности

Диаграмма направленности антенны любой бортовой РЛС состоит не только из главного, но и из боковых лепестков конечной ширины. Поэтому происходит неполная компенсация эффекта движения в РЛС с внутренней когерентностью. Полная компенсация получается лишь для направления максимума главного лепестка ДНА. Кроме того, наличие боковых лепестков при движении РЛС вызывает расширение спектра отраженного сигнала от подстилающей поверхности. Исследование этого вопроса привело к разработке РЛС квазинепрерывного излучения малой скважности с низкой, средней и высокой частотами повторения, которые наилучшим образом выделяют сигналы воздушных целей на фоне отражений от подстилающей поверхности [98]. Основной трудностью анализа свойств отраженных подстилающей поверхностью сигналов помех является расчет их спектрального состава - спектра помех земли.

Как было показано в ряде работ [1, 95-97], при определении спектра пассивных помех отражений от поверхности земли при движении РЛС следует учитывать не только характеристики отражающей поверхности и кинематику движения РЛС, но и форму ДНА, включая боковые лепестки. Естественно, в этом случае от аппроксимации формы ДНА как в области главного лепестка, так и в области боковых лепестков зависят простота расчета и соответствие рассчитанного спектра реальному.

Рассмотрим некоторые геометрические соотношения, связанные с движением РЛС. Будем считать при этом, что зондирующий сигнал является непрерывным немодулированным колебанием. Согласно рис. 10.5 РЛС на летательном аппарате в точке О имеет путевую скорость υ, направленную под углом ро к горизонту и под углом β₀ к проекции продольной оси самолета на горизонтальную плоскость.

Если рассматривать точку М на поверхности земли, направление на которую ОМ составляет с направлением вектора путевой скорости ОС угол γ_M, то доплеровская поправка на частоту составит f_дM = (2υ/c) f₀ cos γ_M или f_дM = (2υ/c) f₀ cos α_M cos β_M. При этом геометрическим местом точек, имеющих такую же доплеровскую поправку, будет являться конус, на поверхности которого лежат точки, отвечающие условию cos γ_M = const. Пересечение конической поверхности с поверхностью земли в передней полусфере летательного аппарата возможно, если γ > +β₀, где знак "+" перед β соответствует направлению υ вверх от горизонтали (и наоборот).

В зависимости от соотношения γ и β₀ в этом случае линия пересечения конуса и поверхности земли (плоскости) будет описываться различными соотношениями. В частности, при β₀ = 0 это будет гипербола, при β₀ ≥ 2γ - эллипс и, наконец, при β₀ = γ - парабола. Обычно рабочим соотношением β₀ и γ является 0 ≤ β₀ < 2γ, и поэтому на поверхности земли образуется линия равных доплеровских частот "изодопа" в виде гиперболы. Меняя угол γ, получаем семейство конических поверхностей и, как следствие, семейство "изодоп" на поверхности земли. При переходе в режим когерентно-импульсного излучения необходимо учитывать наличие "слепых" скоростей, соответствующих отсутствию модуляции импульсов при когерентном сравнении отраженного и опорного сигналов [1]. Если использовать известное соотношение

где n = 1, 2, 3, ... , то согласно рис. 10.5

т. е. υ cos γ_n = nλ/2Т_п, откуда получаем

где γ_n углы, при которых образуются "слепые" скорости. Значит, при любом n будет существовать система соосных конусов "слепых" скоростей, а на поверхности земли - система гипербол "слепых" скоростей

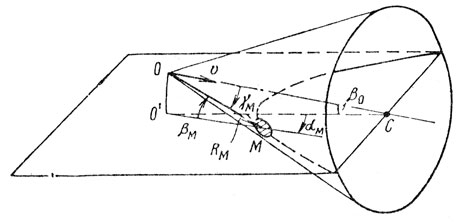
Рис. 10.5

Что касается аппроксимации ДНА, то она определяет точность соответствия реальных спектров помех рассчитанным. Наиболее простой является аппроксимация ДНА [1] в виде главного лепестка и сплошной сферы боковых лепестков. При этом могут использоваться обычные способы описания формы главного лепестка в виде отрезка косинусоиды, отрезка функции Бесселя или, наконец, гауссовской кривой.

Более точное приближение дает аппроксимация ДНА в виде главного лепестка, первых боковых лепестков и сплошной сферы остальных боковых лепестков. Конечно, наилучшей аппроксимацией будет задание точной формы всей ДНА, получаемой по результатам измерении или предварительных расчетов.

При расчете мощности и спектра отражений от поверхности земли можно использовать геометрические представления. На рис. 10.6 представлено расположение цели, РЛС и участка мешающих отражений Причем начало координат совмещено с самолетом-носителем РЛС. В этом случае в режиме импульсного излучения высокой скважности при выборе периода повторения из условия однозначного измерения дальности

сигналы и помехи достигают одновременно входа радиолокационного приемника с поверхности сферы, описываемой уравнением

где R_M - радиус сферы.

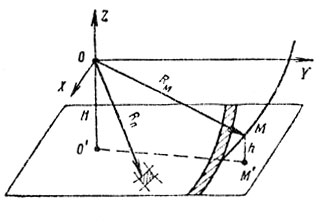
Рис. 10.6

Поскольку источником помех является поверхность земли, которую в первом приближении можно задавать плоскостью, параллельной плоскости XOY и находящейся на расстоянии H ниже ее, то геометрическим местом точек поверхности земли, сигналы от которых одновременно достигают входа приемника, будет являться окружность, задаваемая уравнением

В режиме импульсного излучения малой скважности с высокой частотой повторения, при которой период повторения не обеспечивает однозначного измерения дальности R_max > cT_п/2, уравнение переписывается в следующем виде:

где К = 1, 2, 3, ...

Таким образом, в этом случае на поверхности земли образуется система окружностей, точки которых являются источником отражений, формирующих сигнал пассивной помехи на входе приемника. С учетом конечной длительности зондирующего импульса τ, на поверхности земли образуется система колец, общая поверхность которых и будет пропорциональна интенсивности пассивных помех (рис. 10.7). Однако не нужно забывать и характеристики рассеяния конкретной земной поверхности, а также возможную неоднородность поверхности в пределах зоны облучения РЛС под летательным аппаратом.

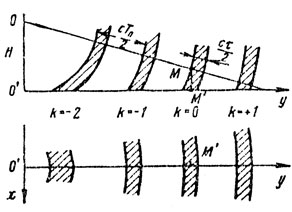
Рис. 10.7

Главную же неравномерность в интенсивность отражений от земли вносит неравномерность излучения и приема антенны в зависимости от ее направленности. При самой простой аппроксимации (главный лепесток и сфера боковых лепестков) более интенсивные отражения будут приходить от эллипса поверхности земли в пределах главного лепестка (рис. 10.8).

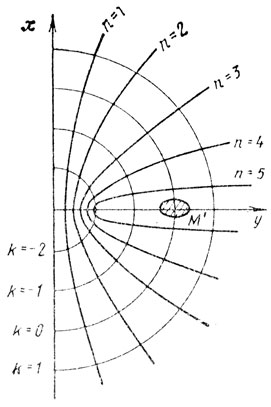
Рис. 10.8

Для анализа спектрального состава суммарного сигнала пассивных помех необходимо совместить построения рис. 10.5 и 10.6 для определенного режима излучений. Тогда поверхность земли будет рассечена семействами линий равных расстояний до РЛС - окружности (k = 0, ±1, ±2, ...) и равных доплеровских частот - гиперболы (n = 0, ±1, ±2, ...) (рис. 10.8). Стробирование по дальности и фильтрации по частоте (стробирование по скорости) при обработке сигналов в РЛС могут быть учтены расширением линий семейств в зависимости от длительности селекторного импульса ΔR = (сτ/2)(√(R² + H²/R)) и от полосы доплеровского фильтра ΔF (соответствующей длительности селекторного импульса по радиальной скорости). При расположении цели не в плоскости путевой скорости картина, отражений будет определяться рис. 10.9.

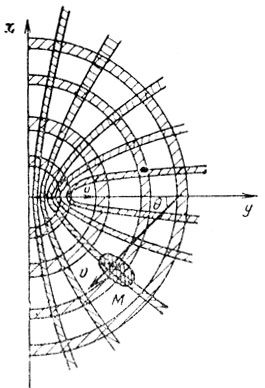
Рис. 10.9

Кроме того, важна взаимная ориентация путевых скоростей υ летательного аппарата, находящегося в точке О, продольная ось которого направлена всегда по оси O'Y и υ_ц объекта, находящегося в пределах главного лепестка в точке М, ориентированного произвольно. Можно учесть взаимную ориентацию векторов скоростей υ и υ_ц углом θ. Тогда при θ < ±90° происходит сближение в передней полусфере с целью и векторы скорости складываются:

При 90° < θ < 270° происходит сближение с целью в задней полусфере цели и векторы скорости вычитаются:

При монохроматическом непрерывном излучении ширина спектра будет определяться максимальной радиальной скоростью относительно земли, т. е. значением путевой скорости, поскольку в пределах сферы боковых лепестков происходят передача и прием сигналов со всех направлений. Таким образом образуется непрерывный участок спектра отражений шириной ±2υ/λ, форма которого связана с диаграммой обратного рассеяния конкретного типа местности и зависимостью интенсивности отраженных сигналов от дальности до участков отражении. Кроме того, возникает пик в спектре отражений за счет большей интенсивности отражений по главному лепестку ДНА. Методика расчета спектра пассивных помех излагается в ряде работ [8, 95-98].

В общем случае энергетический спектр отражений от земли может быть определен на основании соотношения

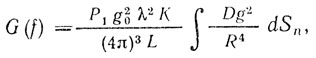(10.12)

где согласно рис. 10.10: dS_n - проекция ab'c'd' элемента площади земли a, b, c, d на плоскость, перпендикулярную Oa и равную

γ - угол между вектором скорости υ и направлением на точку а; θ - угол поворота плоскости Oba вокруг вектора υ относительно вертикальной плоскости; Р₁ - мощность передатчика; g₀ - максимальный коэффициент усиления антенны; g - нормированная диаграмма направленности по мощности; K - коэффициент отражения от поверхности земли; L - потери в системе; D - диаграмма обратного рассеяния земли.

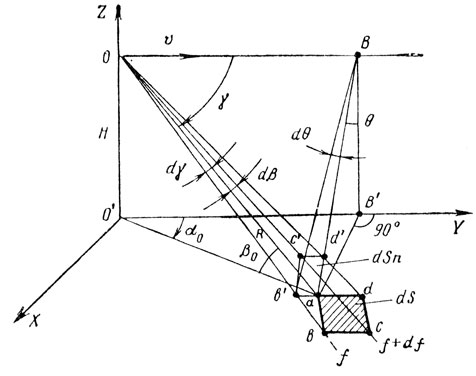
Рис. 10.10

Поскольку f_д = 2υ/c f₀ cos γ = f_дц cos γ и df_д = f_дц sin γ dγ, то

dS_n = R²/f_дц dfdθ.

Переходя к диаграммам направленности и обратного рассеяния, записанным в координатах γ, θ, т. е. g(γ, θ) и D(γ, θ), получаем с учетом R = H/cos θ sin γ

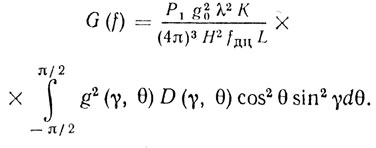(10.13)

Задаваясь конкретными g(γ, θ) и D(γ, θ), можно вычислить энергетический спектр пассивных помех отражений от поверхности земли.

На рис. 10.11 показаны примеры спектральных плотностей помех [8], рассчитанных для реальных g(γ, θ) и D(γ, θ) при различных положениях главного лепестка ДНА.

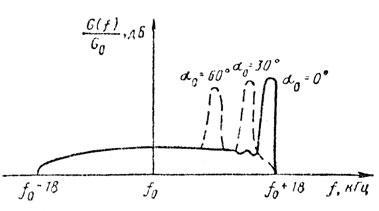
Рис. 10.11

Таким образом, при сближении с целью в передней полусфере с учетом 1851 доплеровская поправка сигнала цели f_дц всегда больше максимальной доплеровской поправки в спектре отражений от земли f_{дз max} и спектры полезного сигнала (а) и пассивной помехи не перекрываются (рис. 10.12). При сближении с целью в задней полусфере f_дц < f_дз спектры полезного сигнала цели (б, в) и пассивных помех перекрываются. Если |υ_ц cos θ| < |υ|, то при υ_∑ > 0 летательный аппарат догоняет цель и спектр сигнала (б) лежит в области спектра помех в пределах от f₀ до f₀ + f_{дз max}.

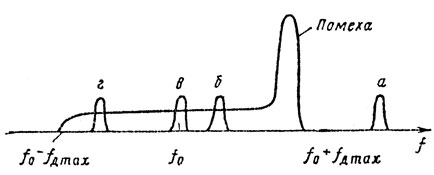
Рис. 10.12

Если |υ_д cos θ| = |υ|, то при υ_∑ = 0 летательный аппарат и цель перемещаются на одинаковое расстояние в единицу времени и спектр сигнала (в) совпадает с несущей частотой в спектре помех. Наконец, при |υ_ц cos θ| > |υ| получаем υ_∑ > 0, т. е. летательный аппарат отстает от цели и поэтому спектр полезного сигнала (г) лежит в области помех с частотами, меньшими f₀.

При переходе к режиму когерентно-импульсного излучения следует учесть появление в спектре помехи составляющих частоты повторения импульсов, влияние на спектр помех формы импульса и уменьшение интенсивности помех за счет того, что суммируется помеха лишь с соответствующих колец дальности (рис. 10.7). Пренебрегая влиянием формы импульсов и считая, что она близка к прямоугольной, можно оценить ослабление мощности помех на каждой составляющей частоты повторения [1]. Пронумеровав гармоники частоты повторения 1, 2, 3, ..., а несущему колебанию присвоив нулевой номер, получим простое соотношение для оценки ослабления интенсивности помехи на каждой гармонике частоты повторения:

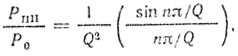(10.14)

где Q - скважность излучения, равная отношению периода повторения к длительности импульса:

Q = T_п/τ = (τF_п)^-1.

В [98] приведен метод расчета мощности помех отражения от земли, позволяющий составить программу расчета помех на выходе канала обработки РЛС. На рис. 10.13 приведен чертеж расположения дифференциального элемента отражения dS, образованного изодопами f_д и f_д + df_д и линиями равных расстояний R и R + dR. Таким образом, площадь отражений этого участка

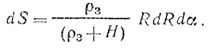
На рис. 10.13 приняты следующие обозначения; Z_з, Y_з, X_з - система геоцентрических координат; X, Y, Z - система координат относительно проекции ЛА на поверхность земли - точка О; ξ - угол наклона вектора скорости ЛА вертикальной плоскости YZ; γ_М - угол между направлением на точку М и вектором скорости; β_М - угол наклона луча антенны по вертикали; α_М - азимут точки М; β_с - угол скольжения; Н - высота ЛА; ρ_з - радиус кривизны земли; RM = R - дальность точки М.

По теореме косинусов sin β_М = H/R + (R² + H²)/[2R (ρ_з + H)] и sin β_с = H/R - (R² - H²)/(2Rρ_з), а cos γ_M выражается через углы ξ, β_M и α_M соотношением

Таким образом, мощность, отраженная элементом поверхности dS,

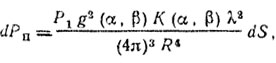(10.15)

где К(α, β) - коэффициент отражения поверхности.

Подставляя в (10.15) значение dS, получаем

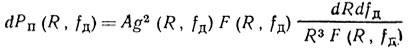
где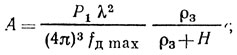

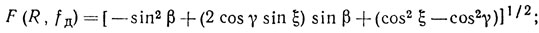
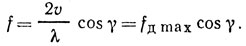
Функция F(R, f_д) существует лишь для неотрицательных значений подкоренного выражения, т. е. при условии

Условие F(R, f_д) = 0 ограничивает область в координатах R, f_д, в которой обеспечивается пересечение линий R = const и f_д = const, а значит, и существование элемента dS.

В импульсно-доплеровских системах с высокой и средней частотами повторения обычно канал обработки после УПЧ с полосой Δf = 1/τ содержит (см. гл. 2) набор селекторов дальности, стробируемых импульсами U_си(t - nТ_п - 2R_lk/c), фильтр с переходной характеристикой h_l(t), весовой усилитель пачки импульсов с весовой функцией g_l(t) и набор доплеровских фильтров с переходной характеристикой h_j(t). Здесь обозначено: l - номер селектора дальности; j - номер доплеровского фильтра; n - номер периода повторения; k - номер кольца дальности.

В результате общая (сквозная) обработка в канале задается соотношением

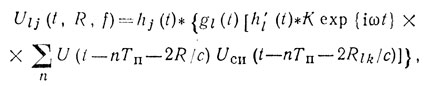
где ∑_n (t - nТ_п - 2R/c) - входная последовательность импульсов от поверхности с расстояния R. Расчет с использованием этого соотношения в предположении ступенчатого сканирования антенны, неизменности числа импульсов в пачке, одинаковой формы селекторных импульсов и частотных характеристик фильтров все-таки оказывается сложным и требует дополнительных упрощающих допущений [98]. К числу таких допущений относятся:

1) узкополосность частотных характеристик функций h_l(t) и g_l(t) по сравнению с F_п;

2) малость доплеровского набега фазы за время импульса 2υπ/λ << 1;

3) число суммируемых составляющих спектра отражений приближенно должно быть N_υ = 4υT_п/λ;

4) ширина результирующего импульса после стробирования должна соответствовать интервалу дальности ΔR = с (τ + τ_си)/4.

Для прямоугольной формы зондирующего и селекторного импульсов длительностью 1 мкс, периода повторения Т_п = 30 мс, максимальной доплеровской поправки f_{д max} = 2υ/λ = 4,9 кГц, высоты полета H = 7620 м, ширины полосы пропускания доплеровского фильтра Δf = 40 Гц, вектора скорости, расположенного горизонтально, ξ = 0, углов установки антенны α_M = 45°, β_M = 3°, ширины главного лепестка по уровню половинной мощности в обеих плоскостях 3° и коэффициента усиления антенны g₀ = 37,7 дБ, постоянного коэффициента отражения поверхности К(α, β) = К = 0,01 и для гипотетической цели, имеющей эффективную поверхность рассеяния S₀/R⁴ = 2⋅10^-13/H², был произведен расчет на ЦЭВМ. Результаты расчета показаны на рис. 10.14 в виде зависимости отношения спектральных составляющих энергетического спектра отражений от земной поверхности к мощности сигнала цели от частоты, нормированной к значению f_{д max}.

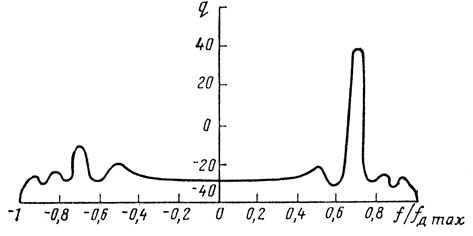
Рис. 10.14

В режиме когерентно-импульсного излучения чрезвычайно важен выбор частоты повторения импульсов. Дело в том, что около каждой гармоники частоты повторения об разуется полоса энергетического спектра помех (рис. 10.11), ширина которой определяется величиной 2f_{дз max}. При частоте повторения, меньшей этой величины, спектры помех соседних гармоник частоты повторения перекроются, произойдет суммирование и увеличение интенсивности спектра помех отражений от земли. При сближении с целью в передней полусфере можно существенно улучшить отношение мощностей сигнала и помехи, выбрав частоту повторения из условия обеспечения в спектре отраженных сигналов зоны, свободной от составляющих пассивных помех от земли (рис. 10.15):

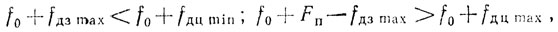(10.16)

где f_{дз max} - максимальная доплеровская поправка отражений земли; f_{дц min} - минимальная доплеровская поправка сигнала цели; f_{дц max} - максимальная доплеровская поправка сигнала цели.

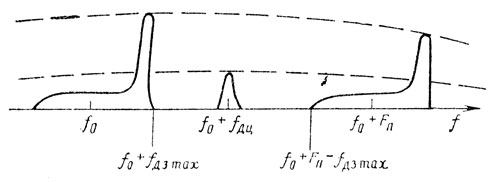
Рис. 10.15

Анализируя систему неравенств, заключаем, что пер вое неравенство не всегда можно обеспечить, поскольку f_{дц min} при сближении в передней полусфере цели может уменьшаться до нуля. Поэтому имеет смысл лишь второе неравенство, из которого следует

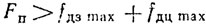
или, если перейти к скоростям движения,

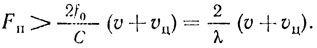(11.17)

Расчеты по этому соотношению частоты повторения F_п и однозначно измеряемой дальности R_max для различных типов ЛА и целей показывают, что в когерентно-импульсных радиолокаторах с селекцией сигнала цели по скорости частота повторения, выбираемая из условия (10.17), оказывается высокой и не обеспечивает однозначного измерения дальности в необходимых пределах (сотни и тысячи километров). В таких РЛС обеспечивается однозначность измерения скорости (селекция по скорости) и не обеспечивается однозначность измерения дальности.

Интервалы между зондирующими импульсами получаются небольшими - от 10 до 100 мкс. При этом длительность зондирующих импульсов остается фиксированной и в среднем не выходящей за пределы интервала 0,1-1 мкс. Это значит, что скважность излучения оказывается малой, что позволяет относить эти станции к классу РЛС, работающих в режиме малой скважности с высокой частотой повторения или к классу квазинепрерывных РЛС. Их также называют когерентно-импульсными с высокой частотой повторения или импульсно-доплеровскими. Необходимость глубокой развязки приемного и передающего трактов обычно решается путем стробирования каскадов приемника. При этом вся дистанция, подлежащая просмотру, оказывается разбитой на участки, соответствующие интервалам излучения передатчика и запирания приемника, и участки пауз, когда приемник открыт. При сближении с целью или удаления от цели, т. е. при t_R = t_R0 ± αt, сигнал от цели начинает периодически частично и полностью перекрывать участки времени запертого приемника, вследствие чего возникают потери мощности сигнала, зависящие от скважности излучения [1]. Это явление по аналогии с явлением "слепых" скоростей носит название эффекта "слепых" дальностей. Зависимость мощности на входе приемника при скважности Q = 2 и 5 показана на рис. 10.16, а и б.

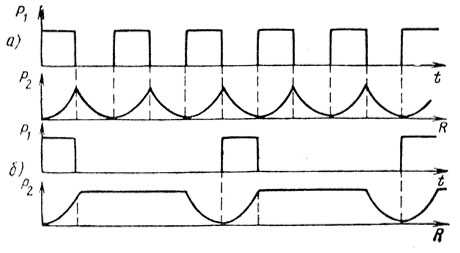
Рис. 10.16

При сближении с целью в задней полусфере цели, как отмечалось выше, спектры сигналов цели и пассивных помех перекрываются и при этом нет необходимости выбирать высокую частоту повторения. Таким образом приходим к когерентно-импульсной РЛС с частотой повторения, выбираемой из условия однозначного определения дальности, с высокой скважностью излучения. При этом режиме отсутствуют "слепые" дальности, но имеются "слепые" скорости, а боковые составляющие спектра пассивных помех перекрываются.