2.3. Гармонический анализ периодических колебаний

При разложении периодического колебания s(t) в ряд Фурье по тригонометрическим функциям в качестве ортогональной системы берут

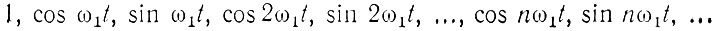(2.18)

или

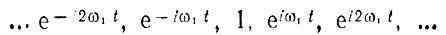(2.19)

Интервал ортогональности в обоих случаях совпадает с периодом Т = 2π/ω₁ функции s(t).

Система функций (2.18) приводит к тригонометрической форме ряда Фурье, а система (2.19) - к комплексной форме. Между этими двумя формами существует простая связь.

Воспользуемся сначала ортогональной системой (2.19), Тогда ряд Фурье должен быть записан в форме

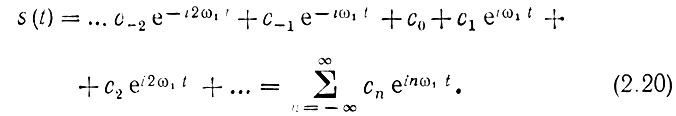
Коэффициенты Фурье с_n легко определяют с помощью формул, приведенных в предыдущем параграфе.

Из формулы (2.5') следует, что

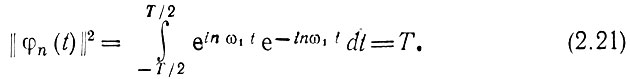
Таким образом, независимо от n норма 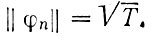Используя формулу (2.9'), получаем

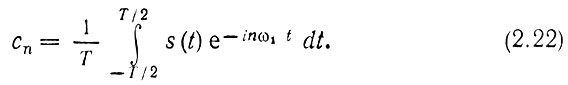
В выражениях (2.21) и (2,22) учтено, что функции е^inω₁t соответствует комплексно-сопряженная функция е^-inω₁t.

Коэффициенты с_n в общем случае являются комплексными величинами. Подставив в (2,22) 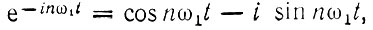получим

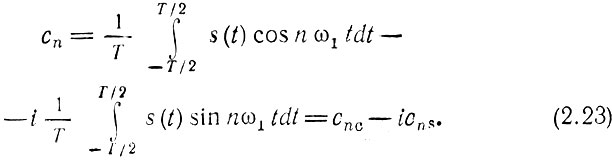
Косинусная (действительная) и синусная (мнимая) части коэффициента с_n определяются формулами

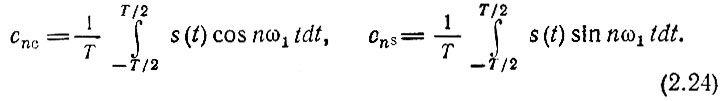
Коэффициенты c_n часто бывает удобно записывать в форме

где

Модуль |с_n| является функцией, четной относительно n, а аргумент θ_n - нечетной (последнее вытекает непосредственно из выражений (2.24), показывающих, что с_nс является четной, а с_ns нечетной функциями n).

Общее выражение (2.20) можно привести к виду

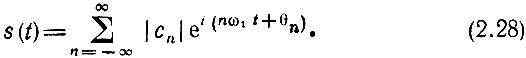
Теперь нетрудно перейти к тригонометрической форме ряда Фурье. Выделив из ряда (2.28) пару слагаемых, соответствующую какому-либо заданному значению |n|, например, |n| = 2, и учтя соотношения θ_-2 = -θ₂, |c_-2| = |с₂|, получим для суммы этих слагаемых

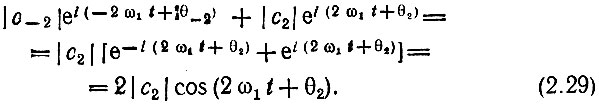
Отсюда видно,что при переходе к тригонометрической форме ряд (2.28) необходимо записать следующим образом:

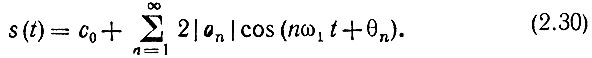
Смысл удвоения коэффициентов Фурье с_n в тригонометрическом ряду при n ≥ 1 становится ясным из рассмотрения векторной диаграммы (рис. 2.1), соответствующей (2.29) при |n| = 2. Вещественная функция 2|c_n|cos(nω₁t + θ_n) получается как сумма проекций на горизонтальную ось ОВ двух векторов длиной |с_n|, вращающихся с угловой частотой |n|ω₁ во взаимно противоположных направлениях. Вектор, вращающийся против часовой стрелки, соответствует положительной частоте, а вектор, вращающийся по часовой стрелке, - отрицательной. После перехода к тригонометрической форме понятие "отрицательная частота" теряет смысл. Коэффициент с₀ не удваивается, так как в спектре периодического сигнала составляющая с нулевой частотой не имеет "дублера".

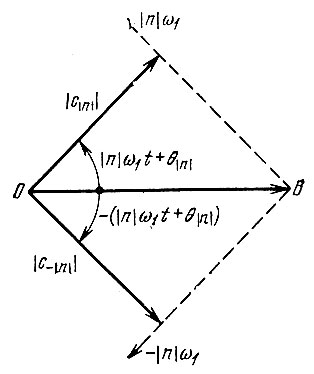
Рис. 2.1. Представление гармонического колебания в виде двух комплексных составляющих: с положительной и отрицательной частотами

Вместо выражения (2.30) в математической и радиотехнической литературе часто встречается следующая форма записи:

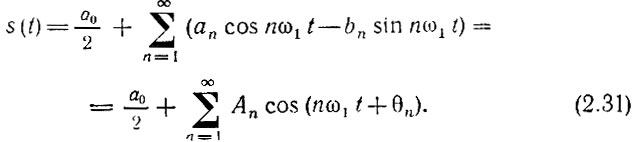
Из сопоставления выражений (2.31) и (2.30) видно, что амплитуда n-й гармоники А_n связана с коэффициентом |с_n| ряда (2.28) соотношением

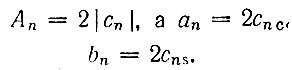
Таким образом, для всех положительных значений n (включая и n = 0)

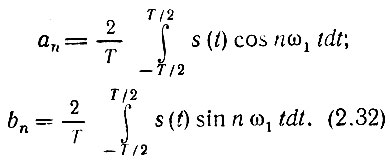
Если колебание представляет собой функцию, четную относительно t, т. е. s(t) = s (-t), в тригонометрической записи ряда остаются только косинусоидальные члены, так как коэффициенты b_n в соответствии с формулой (2.32) обращаются в нуль. Для нечетной относительно t функции s(t), наоборот, в нуль обращаются коэффициенты b_n и ряд состоит только из синусоидальных членов.

Две характеристики - амплитудная и фазовая, т. е. модули и аргументы комплексных коэффициентов ряда Фурье, полностью определяют структуру частотного спектра периодического колебания. Наглядное представление о "ширине" спектра дает графическое изображение спектра амплитуд. В качестве примера на рис. 2.2, а построен спектр коэффициентов |с_n|, а на рис. 2.2, б - спектр амплитуд А_n - 2|с_n| для одного и того же периодического колебания. Для исчерпывающей характеристики спектра подобные построения должны быть дополнены заданием начальных фаз отдельных гармоник.

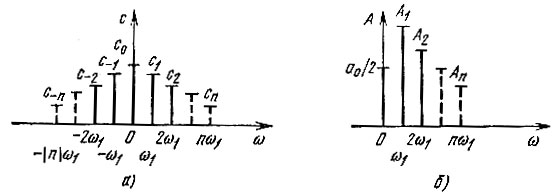
Рис. 2.2. Коэффициенты комплексного (а) и тригонометрического (б) ряда Фурье периодической функции времени

Спектр периодической функции называется линейчатым или дискретным, так как состоит из отдельных линий, соответствующих дискретным частотам 0, ω₁, ω₂ = 2ω₁ ω₃ = 3ω₁ и т. д.

Использование для гармонического анализа сложных периодических колебаний рядов Фурье в сочетании с принципом наложения представляет собой эффективное средство для изучения влияния линейных систем на прохождение сигналов. Следует, правда, отметить, что определение колебания на выходе системы по сумме гармоник с заданными амплитудами и фазами является непростой задачей, особенно если не обеспечивается быстрая сходимость ряда Фурье, представляющего колебание. Наиболее распространенные в радиотехнике сигналы не отвечают этому условию, и для удовлетворительного воспроизведения формы сигналов обычно необходимо суммировать большое число гармоник. Поэтому следует считать, что в случае сложных периодических сигналов метод ряда Фурье удобнее применять для анализа сигналов, нежели для их синтеза.