2.4. Спектры простейших периодических колебаний

Рассмотрим несколько примеров периодических колебаний, часто используемых в различных радиотехнических устройствах.

1. Прямоугольное колебание

Подобное колебание, часто называемое меандром^*, находит широкое применение в измерительной технике.

^* (Меандр - греческое слово, обозначающее орнамент.)

При выборе начала отсчета времени по рис. 2.3, а функция является нечетной, а по рис. 2.3, б - четной. Применяя формулы (2.24), находим для колебания, изображенного на рис, 2.3, а,

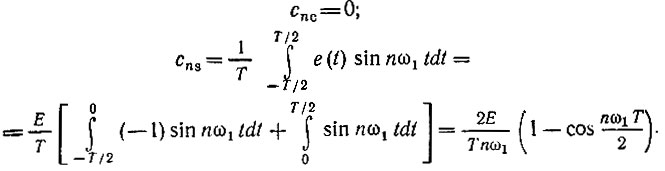
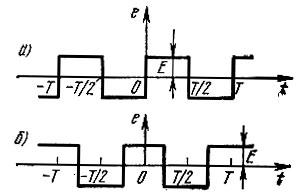
Рис. 2.3. Периодическое колебание прямоугольной формы (меандр)

Учитывая, что Tω₁ = 2π, получаем

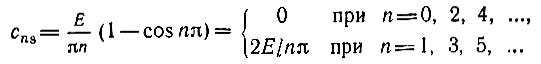
Начальные фазы θ_n в соответствии с (2.27) равны -π/2 для всех гармоник.

Запишем ряд Фурье в тригонометрической форме

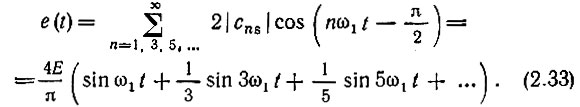
Спектр коэффициентов |c_n| комплексного ряда Фурье показан на рис. 2.4, а, а тригонометрического ряда - на рис. 2.4, б.

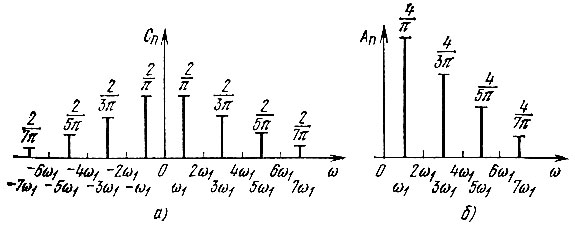
Рис. 2.4. Коэффициенты комплексного (а) и тригонометрического (б) ряда Фурье колебания, показанного на рис. 2.3

При отсчете времени от середины импульса (рис. 2.3, б) функция является четной относительно t и для нее

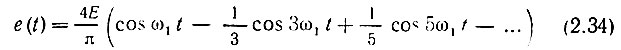
Графики 1-й (n = 1) и 3-й (n = 3) гармоник и их суммы изображены на рис. 2.5, а. На рис. 2.5, б эта сумма дополнена пятой гармоникой, а на рис. 2.5, в - седьмой.

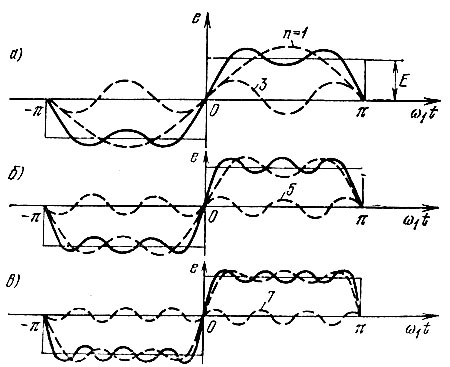
Рис. 2.5. Суммирование 1-й и 3-й гармоник (а), 1, 3 и 5-й гармоник (б), 1, 3, 5 и 7-й гармоник (в) колебания, показанного на рис. 2.3

С увеличением числа суммируемых гармоник сумма ряда приближается к функции е(t) всюду, кроме точек разрыва функции, где образуется выброс. При n → ∞ величина этого выброса равна 1,18E, т. е. сумма ряда отличается от заданной функции на 18%. Этот дефект сходимости в математике получил название явления Гиббса. Несмотря на то, что в рассматриваемом случае ряд Фурье не сходится к разлагаемой функции е(t) в точках ее разрыва, ряд сходится в среднем, поскольку при n → ∞ выбросы являются бесконечно узкими и не вносят никакого вклада в величину интеграла (2.13).

2. Пилообразное колебание

С подобными функциями часто приходится иметь дело в устройствах для развертки изображения в осциллографах. Так как эта функция является нечетной, ряд Фурье для нее содержит только синусоидальные члены. С помощью формул (2.24)-(2.31) нетрудно определить коэффициенты ряда Фурье. Опуская эти выкладки, напишем окончательное выражение для ряда

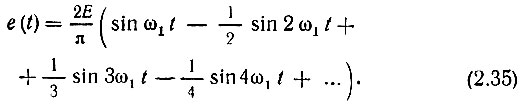
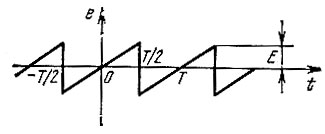
Рис. 2.6. Периодическое колебание пилообразной формы

Как видим, амплитуды гармоник убывают по закону 1/n, где n = 1, 2, 3, ... На рис. 2.7 показан график суммы первых пяти гармоник (в увеличенном масштабе).

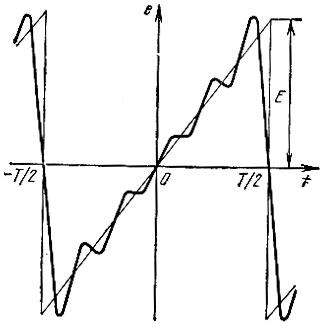
Рис. 2.7. Сумма первых пяти гармоник колебания, показанного на рис. 2.6

3. Последовательность униполярных треугольных импульсов

Ряд Фурье для этой функции имеет следующий вид:

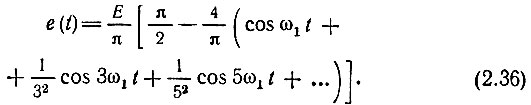
На рис. 2.8 изображена сумма первых трех членов этого ряда. В данном случае отметим более быстрое убывание амплитуд гармоник, чем в предыдущих примерах. Это объясняется отсутствием разрывов (скачков) в функции.

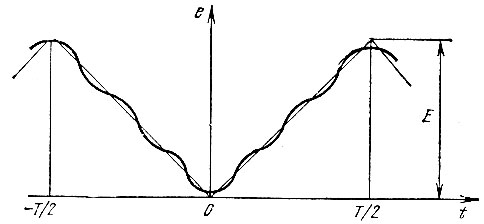
Рис. 2.8. Сумма трех первых гармоник периодической функции

4. Последовательность униполярных прямоугольных импульсов

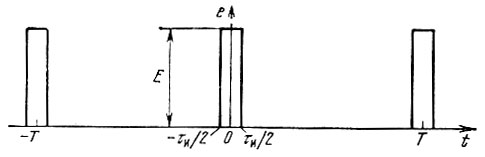
Рис. 2.9. Периодическая последовательность прямоугольных импульсов с большой скважностью

Применяя формулы (2.32), находим среднее значение (постоянную составляющую)

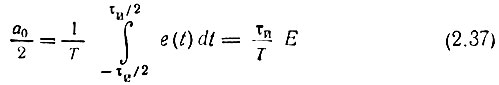
и коэффициент n-й гармоники

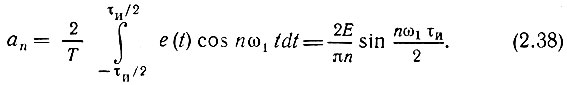
Так как функция e(t) четная, b_n = 0 и A_n = a_n. таким образом,

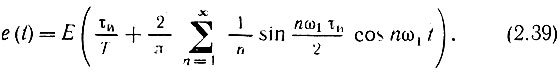
Величина N = T/τ_и называется скважностью импульсной последовательности. При больших значениях N спектр сигнала содержит очень большое число медленно убывающих по амплитуде гармоник (рис. 2.10). Расстояние между спектральными линиями очень мало, а амплитуды соседних гармоник близки по величине. Это наглядно вытекает из формулы (2.38), которую в данном случае удобно представить в несколько измененном виде

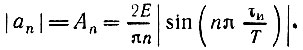
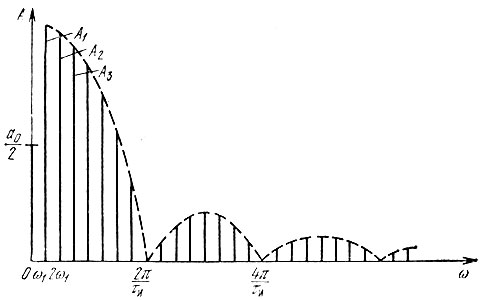
Рис. 2.10. Спектр импульсной последовательности, показанной на рис. 2.9

При малых значениях n можно считать

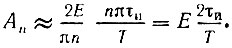
Постоянная составляющая, равная а₀/2 = Eτ_и/T, вдвое меньше амплитуды первой гармоники. При построении спектра коэффициентов |с_n| величина с₀ приближенно равнялась бы |c₁|.