2.5. Распределение мощности в спектре периодического колебания

Пусть колебание s(t) (ток, напряжение) представляет собой сложную периодическую функцию времени с периодом Т.

Энергия такого колебания, длящегося от t = -∞ до t = ∞, бесконечно велика. Основной интерес представляет средняя мощность периодического колебания и распределение этой мощности между отдельными гармониками. Очевидно, что средняя мощность колебания, рассматриваемого на всей оси времени, совпадает с мощностью, средней за один период Т. Поэтому можно воспользоваться формулой (2.17), в которой под коэффициентами оп следует подразумевать коэффициенты ряда (2.20), под интервалом ортогональности t₂ - t₁ - величину периода Т, а под нормой ||φ_n|| - величину 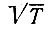[см. формулу (2.21)].

Таким образом, средняя мощность периодического колебания

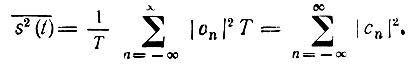
Используя тригонометрическую форму ряда Фурье и учитывая, что 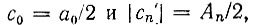получаем

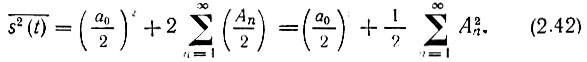
Если s(t) представляет собой ток i(t), то при прохождении его через сопротивление r выделяется мощность (средняя)

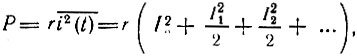
где I₀ = а₀/2 - постоянная составляющая, а I_n = А_n - амплитуда n-й гармоники тока i(t).

Итак, полная мощность равна сумме средних мощностей, выделяемых отдельно постоянной составляющей I₀ и гармониками с амплитудами I₁, I₂, ... Это означает, что средняя мощность не зависит от фаз отдельных гармоник.