2.6. Гармонический анализ непериодических колебаний

Изложенный в § 2.3 гармонический анализ периодических колебаний можно распространить на непериодические колебания. Пусть такое колебание s(t) задано в виде некоторой функции, отличной от нуля в промежутке (t₁, t₂) (рис. 2.11).

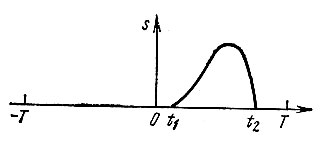
Рис. 2.11. Одиночный импульс

Выделив произвольный отрезок времени Т, включающий в себя промежуток (t₁, t₂), мы можем представить заданное колебание в виде ряда Фурье

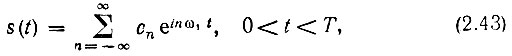
где ω₁ = 2π/Т, а коэффициенты с_n в соответствии с формулой (2.22)

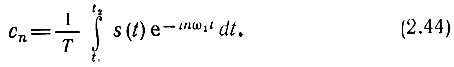
Подставив (2.44) в (2.43), получим

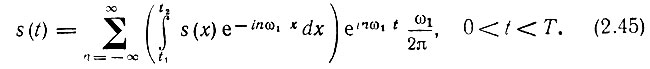
Здесь учтено, что Т = 2π/ω₁.

Вне отрезка (0, Т) ряд (2.43) определяет функцию s(t) = s(t ± kT), где k - целое число, т. е. периодическую функцию, полученную повторением s(t) вправо и влево с периодом Т. Для того чтобы вне отрезка (0, Т) функция равнялась нулю, величина Т должна быть бесконечно большой. Но чем больше отрезок T, выбранный в качестве периода, тем меньше коэффициенты с_n. Устремляя Т к бесконечности, в пределе получаем бесконечно малые амплитуды гармонических составляющих, сумма которых изображает исходную непериодическую функцию s(t), заданную в интервале t₁ < t < t₂ (рис. 2.11). Число гармонических составляющих, входящих в ряд Фурье, будет при этом бесконечно большим, так как при Т → ∞ основная частота функции ω₁ = 2π/Т → 0. Иными словами, расстояние между спектральными линиями (см. рис. 2.2), равное основной частоте ω₁, становится бесконечно малым, а спектр - сплошным.

Поэтому можно в выражении (2.45) заменить ω₁ на dω, nω₁, на текущую частоту ω, а операцию суммирования - операцией интегрирования.

Таким образом, приходим к двойному интегралу Фурье

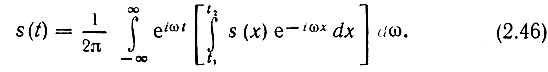
Внутренний интеграл, являющийся функцией ω,

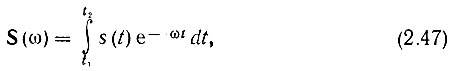
называется спектральной плотностью или спектральной характеристикой функции s(t).

В общем случае, когда пределы t₁ и t₂ не уточнены, спектральная плотность записывается в форме

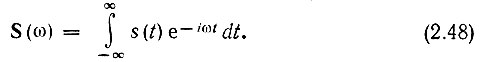
После подстановки (2.48) в выражение (2.46) получаем

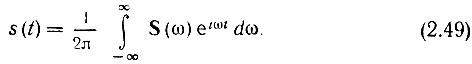
Выражения (2.48) и (2.49) называются соответственно прямым и обратным преобразованиями Фурье.

Выражение (2.48) отличается от (2.22) только отсутствием множителя 1/T. Следовательно, спектральная плотность S(ω) обладает всеми основными свойствами коэффициентов с_n комплексного ряда Фурье. По аналогии с (2.23) и (2.24) можно написать

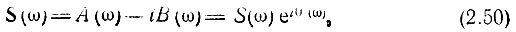
где

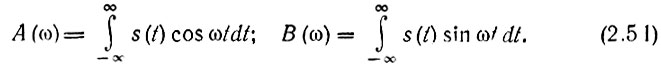
Модуль и аргумент спектральной плотности определяются выражениями

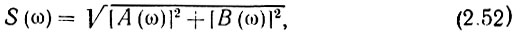
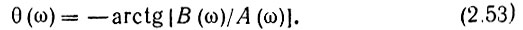
Первое из этих выражений можно рассматривать как амплитудно-частотную, а второе - как фазочастотную характеристику сплошного спектра непериодического колебания s(t).

Как и в случае ряда Фурье, S(ω) является четной, а θ(ω) - нечетной функцией частоты ω.

На основании формулы (2.50) нетрудно привести интегральное преобразование (2.49) к тригонометрической форме. Имеем

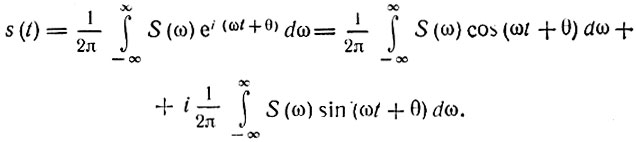
Из четности модуля и нечетности фазы следует, что подынтегральная функция в первом интеграле является четной, а во втором - нечетной относительно ω. Следовательно, второй интеграл равен нулю, и окончательно

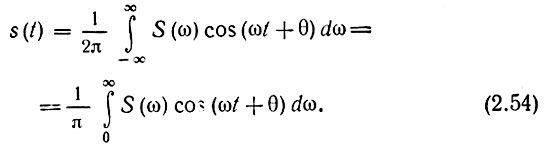
Переход от комплексной формы (2.49) к тригонометрической (2.54) обычно целесообразен в конце анализа; все промежуточные выкладки при применении интеграла Фурье удобнее и проще производить на основании комплексной формы (2.49).

Из сопоставления выражений (2.49) и (2.20) видно, что величина 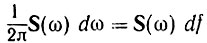имеет смысл коэффициента с_n (бесконечно малого) комплексного ряда Фурье при частоте ω = 2πf. Соответственно из сопоставления выражений (2.54) и (2.31) видно, что величина 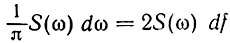имеет смысл амплитуды А_n (бесконечно малой) гармонической составляющей частоты ω = 2πf. Из этих сопоставлений становится ясным смысл термина "спектральная плотность". 2S(ω) есть амплитуда колебания, приходящаяся на 1 Гц в бесконечно узкой полосе частот, включающей в себя рассматриваемую частоту ω.

На основании приведенных выше рассуждений нетрудно установить соотношение между спектрами одиночного импульса и периодической последовательности импульсов.

Пусть задан спектр S₁(ω) одиночного импульса s₁(t) и период повторения Т. Как уже отмечалось выше, спектральная плотность S₁(ω) [см. (2.48)] отличается от коэффициента с_n ряда Фурье периодической последовательности только отсутствием множителя 1/Т [см. формулу (2.22)]. Отсюда следует, что при повторении импульса s₁(t) с периодом Т коэффициенты с_n ряда Фурье для полученной периодической последовательности равны

причем аргумент ω спектральной плотности S₁(ω) следует приравнять частоте nω₁ соответствующей гармоники.

Таким образом,

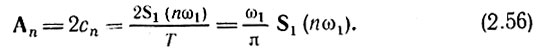
Итак, модуль спектральной плотности одиночного импульса и огибающая линейчатого спектра периодической последовательности, полученной путем повторения заданного импульса, совпадают по форме и отличаются только масштабом.