2.7. Некоторые свойства преобразования Фурье

Между колебанием s(t) и его спектром S(ω) существует однозначное соответствие. Для практических приложений важно установить связь между преобразованием колебания и соответствующим этому преобразованию изменением спектра. Из многочисленных возможных преобразований колебания рассмотрим следующие наиболее важные и часто встречающиеся: сдвиг колебания во времени, изменение масштаба времени, сдвиг спектра колебания по частоте, дифференцирование и интегрирование колебания. Кроме того, будут рассмотрены сложение колебаний, произведение и свертка двух колебаний, а также свойства взаимной обратимости ω и t в преобразованиях Фурье.

1. Сдвиг колебания во времени

Пусть колебание s₁(t) произвольной формы существует на интервале времени от t₁ до t₂ и обладает спектральной плотностью S₁(ω). При задержке этого колебания на величину t₀ (при сохранении его формы) получим новую функцию времени

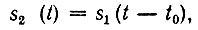
существующую на интервале от t₁ + t₀ до t₂ + t₀.

Спектральная плотность колебания s₂(t) в соответствии с (2.48)

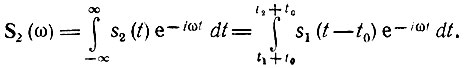
Вводя новую переменную интегрирования τ = t - t₀, получаем

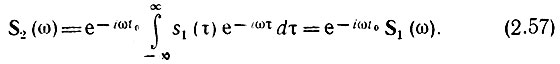
Из этого соотношения видно, что сдвиг во времени функции s(t) на величину ±t₀ приводит к изменению фазовой характеристики спектра S(ω) на величину ±ωt₀. Очевидно и обратное положение: если всем составляющим спектра функции s(t) дать фазовый сдвиг θ(ω) = ±ωt₀, линейно связанный с частотой ω, то функция сдвигается во времени на величину ±t₀.

Амплитудно-частотная характеристика спектра (т. е. модуль спектральной плотности) от положения колебания на оси времени не зависит.

2. Изменение масштаба времени

Пусть колебание s₁(t), изображенное на рис. 2.12 сплошной линией, подверглось сжатию во времени. Новое сжатое колебание s₂(t) (штриховая кривая на рис. 2.12) связано с исходным колебанием соотношением s₂(t) = s₁(nt), n > 1.

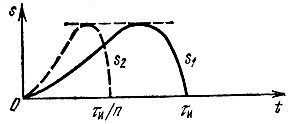
Рис. 2.12. Сжатие сигнала при сохранении его формы и амплитуды

Длительность импульса s₂(t) в n раз меньше, чем у исходного импульса, и равна τ_и/n. Спектральная плотность сжатого импульса

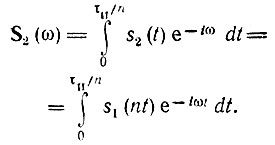
Вводя новую переменную интегрирования τ = nt, получаем

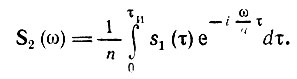
Но интеграл в правой части этого выражения есть не что иное, как спектральная плотность исходного колебания s₁(t) при частоте ω/n, т. е. S₁(ω/n).

Таким образом,

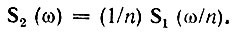
Итак, при сжатии колебания в n раз на временной оси во столько же раз расширяется его спектр на оси частот. Модуль спектральной плотности при этом уменьшается в n раз. Очевидно, что при растягивании колебаний во времени (т. е. при n < 1) имеет место сужение спектра и увеличение модуля спектральной плотности.

3. Смещение спектра колебания

Применим преобразование Фурье (2.48) к произведению s(t) cos(ω₀t + θ₀):

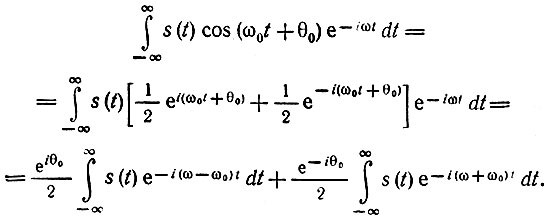
Первый интеграл в правой части есть не что иное, как спектральная плотность функции s(t) при частоте ω-ω₀, а второй интеграл - при частоте ω+ω₀. Поэтому полученное выше соотношение можно записать в форме

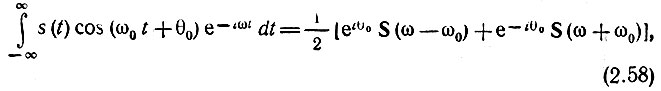
где S(ω) - спектральная плотность колебания s(t).

Из выражения (2.58) вытекает, что расщепление спектра S(ω) на две части, смещенные соответственно на +ω₀ и -ω₀, эквивалентно умножению функции s(t) на гармоническое колебание cosω₀t (при θ₀ = 0).

Более подробно это положение рассматривается в гл. 3 при изучении модулированных колебаний.

4. Дифференцирование и интегрирование колебания

Опуская строгие доказательства, ограничимся простыми рассуждениями. Дифференцирование колебания s₁(t) можно рассматривать как почленное дифференцирование всех гармонических составляющих, входящих в его спектр. Общий вид гармонической составляющей колебания s₁(t) при частоте ω можно представить в форме

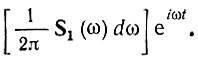
Заключенную в квадратные скобки величину можно рассматривать как амплитуду колебания в полосе dω. [Сравнить последнее выражение с (2.49).]

Дифференцирование по времени t дает

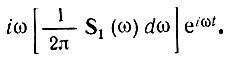
Следовательно, спектральная плотность производной ds₁(t)/dt равна

Аналогично спектральная плотность интеграла 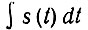равна

5. Сложение колебаний

Так как преобразование Фурье, определяющее спектральную плотность заданной функции времени, является линейным преобразованием, то очевидно, что при сложении колебаний s₁(t), s₂(t), ..., обладающих спектрами S₁(ω), S₂(ω), ..., суммарному колебанию s(t) = s₁(t) + s₂(t) + ... соответствует спектр S(ω) = S₁(ω) + S₂(ω) + ...

6. Произведение двух колебаний

Пусть рассматриваемое колебание s(t) является произведением двух функций времени f(t) и g(t).

Используя общую формулу (2.48), определяем спектр колебания s(t):

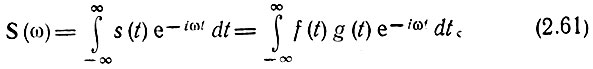
Каждую из функций f(t) и g(t) можно представить в виде интеграла Фурье

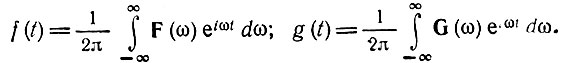
Подставляя в (2.61) второй из этих интегралов, получаем

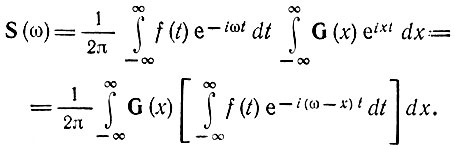
Заключенный в квадратные скобки интеграл представляет собой спектральную плотность функции f(t) при частоте ω - х, т. е. F(ω - х). Следовательно,

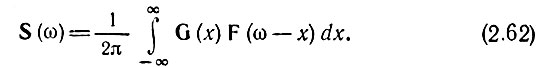
Итак, спектр произведения двух функций времени f(t) и g(t) равен (с коэффициентом 1/2π) свертке их спектров F(ω) и G(ω).

Из выражений (2.61) и (2.62) в частном случае ω = 0 вытекает следующее равенство:

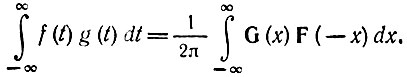
Заменяя в последнем выражении х на ω, получаем

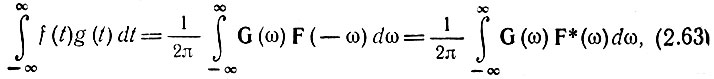
где F^*(ω) = F(-ω) - спектральная функция, комплексно-сопряженная функции F(ω).

Совершенно аналогично можно показать, что произведению двух спектров F(ω) G(ω) = S(ω) соответствует функция времени s(t), являющаяся сверткой функций f(t) и g(t):

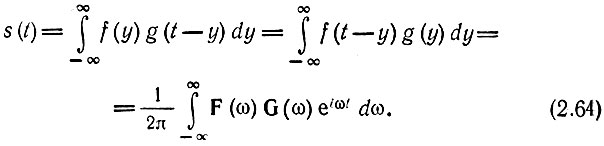
Последнее выражение особенно широко используется при анализе передачи сигналов через линейные цепи. В этом случае функции времени f(t) и g(t) имеют смысл соответственно входного сигнала и импульсной характеристики цепи (см. § 6.3), a F(ω) и G(ω) - спектральной плотности сигнала и передаточной функции цепи.

7. Взаимная заменяемость ω и t в преобразованиях Фурье

Обратимся к общему выражению (2.48) и выясним характер функции S(ω) для различных функций s(t).

а. Пусть s(t) есть функция, четная относительно t. Переписывая выражение (2.48) в виде

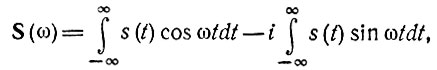
убеждаемся, что при четности s(t) второй интеграл равен нулю, так как произведение s(t) sinωt является функцией, нечетной относительно t, а пределы интегрирования симметричны.

Таким образом, при s(t), четной относительно t, функция S(ω), определяемая первым интегралом, есть функция вещественная и четная относительно ω.

б. Если s(t) нечетна относительно t, то в нуль обращается первый интеграл и

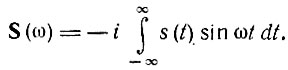
В этом случае S(ω) - нечетная и чисто мнимая функция ω.

в. Если, наконец, s(t) не является четной или нечетной функцией относительно t, то ее можно разложить на две функции: четную s₁(t) и нечетную s₂(t). При этом S(ω) представляет комплексную функцию, причем действительная ее часть четна, а мнимая нечетна относительно ω.

Из п. а вытекает, что при четной функции s(t) можно произвольно выбирать знак перед t. в обратном преобразовании Фурье [формула (2.49)]; выберем знак минус и запишем формулу (2.49) в виде

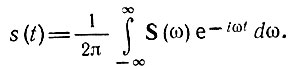
Произведем теперь в последнем интеграле замену переменной интегрирования ω на t и параметра t на ω. Тогда левая часть должна быть записана в виде функции от аргумента ω

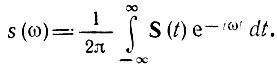
Но интеграл в последнем выражении можно рассматривать как спектральную плотность новой функции S(t), полученной путем замены ω на t в выражении спектральной плотности колебания s(t).

Обозначим эту новую спектральную плотность через S'(ω). Тогда

Этот результат показывает, что переменные ω и t в преобразованиях Фурье взаимно заменимы: если колебанию (четному) s(t) соответствует спектр S(ω), то колебанию S(t) соответствует спектр 2πs(ω).

Пример применения этого правила приводится в п. 3, § 2.9.