2.8. Распределение энергии в спектре непериодического колебания

Для получения выражения, аналогичного (2.42), можно идти двумя путями: исходя из (2.42) совершить предельный переход Т→∞ или воспользоваться результатами предыдущего параграфа.

Рассмотрим второй путь. Для этого воспользуемся выражением (2.63).

Если f(t) и g(t) представляют собой одно и то же колебание

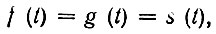
то интеграл

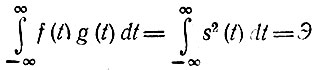
представляет собой полную энергию колебания s(t), а произведение спектральных плотностей

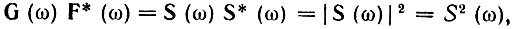
где S(ω) - спектр колебания s(t), а S(ω) - модуль этого спектра.

Таким образом, приходим к окончательному результату

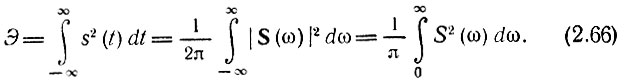
Это важное соотношение, устанавливающее связь между энергией колебания (при сопротивлении 1 Ом) и модулем его спектральной плотности, известно под названием равенства Парсеваля.

Между выражениями (2.42) и (2.66) имеется существенное различие. В § 2.5 речь шла о средней мощности периодического колебания. Операция усреднения осуществлялась делением энергии отрезка колебания за один период на величину Т. В случае же непериодического колебания конечной длительности усреднение энергии за бесконечно большой период дает нуль, и, следовательно, средняя мощность такого колебания равна нулю.

Из выражения (2.66) видно, что величину 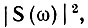имеющую смысл энергии, приходящейся на единицу полосы частот, можно рассматривать как спектральную плотность энергии колебания.