2.10. Соотношение между длительностью сигнала и шириной его спектра

Из предыдущих параграфов уже ясно, что чем меньше длительность сигнала, тем шире его спектр.

Это фундаментальное положение теории сигналов можно установить в общем виде на основе преобразования Фурье

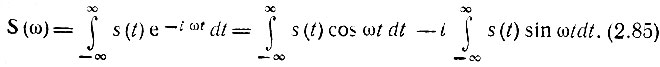
Рассмотрим поведение каждого из интегралов при увеличении ω.

Существует лемма Римана, утверждающая, что если функция s(t) абсолютно интегрируема в некотором конечном промежутке [а, b], то

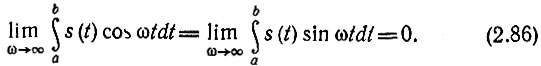
Графически смысл этого утверждения поясняется рис. 2.23, а, на котором изображены некоторый произвольно выбранный сигнал s(t) и гармоническое колебание с частотой ω, и рис. 2.23, б, на котором показано произведение s(t) cosωt [или s(t) sinωt].

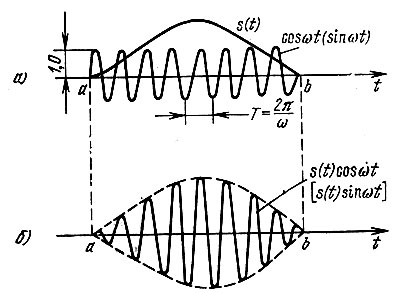
Рис. 2.23. К вопросу о соотношении между длительностью сигнала и шириной его спектра

При достаточно высокой частоте со каждая положительная полуволна на рис. 2.23, б почти полностью компенсируется ближайшей к ней отрицательной полуволной и суммарная площадь s(t) cosωt [или s(t) sinωt] близка к нулю. Под "достаточно высокой частотой" следует подразумевать частоту ω = 2π/Т, при которой период Т достаточно мал по сравнению с длительностью сигнала s(t).

Очевидно, что чем короче сигнал, тем меньше и период Т, соответствующий этому условию. Иными словами,чем короче сигнал, тем выше граничная частота спектра сигнала, Так как нижняя граница спектра примыкает к нулевой частоте (имеются в виду сигналы без высокочастотного заполнения, как, например, на рис. 2.23, а), то спектр получается тем шире, чем короче сигнал. При этом оказывается, что произведение длительности сигнала на ширину его спектра не может быть меньше некоторой постоянной величины. Определение этой величины приводится в приложении 1.