
2.11. Бесконечно короткий импульс с единичной площадью (дельта-функция)
Некоторые из возможных моделей импульса, площадь которого равна единице, изображены на рис. 2.24. Амплитуды всех этих импульсов обратно пропорциональны соответствующим образом определенной длительности импульса. При стремлении длительности к нулю амплитуда обращается в бесконечность, а площадь импульса остается неизменной и равной единице.
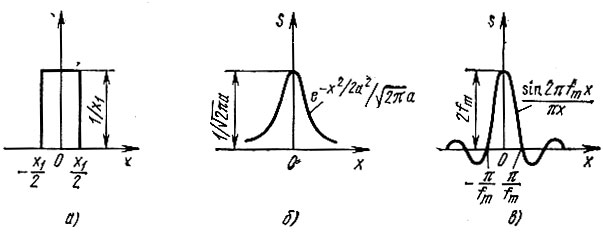
Рис. 2.24. Импульсы, обращающиеся в дельта-функцию при стремлении длительности к нулю
Амплитуду прямоугольного импульса следует приравнять величине 1/x1 (рис. 2.24, а), где x1 - длительность импульса.
При гауссовом импульсе (рис. 2.24, б) амплитуда должна быть приравнена 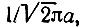 поскольку
поскольку
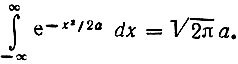
Наконец, для импульса вида sin(2πfmx)/πx (рис. 2.24, в), площадь которого равна единице, амплитуда равна 2fm (при x = 0). Длительность импульса (главного лепестка) обратно пропорциональна параметру fm.
При устремлении параметров х1 и а к нулю, а fm к бесконечности все три изображенные на рис. 2.24 функции можно определить следующим образом:
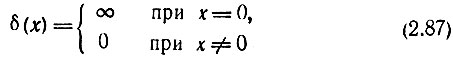
при одновременном условии
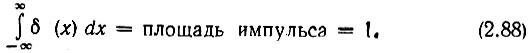
Функция δ(x), обладающая указанными свойствами, называется единичным импульсом, импульсной функцией или дельта-функцией (а также функцией Дирака).
Применительно к исходным функциям, изображенным на рис. 2.24, б и в, дельта-функция должна быть определена выражениями
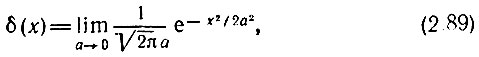
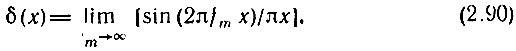
Возможны и другие многочисленные определения δ(х).
При сдвиге импульса по оси х на величину х0 определения (2.87)-(2.90) должны быть записаны в более общей форме
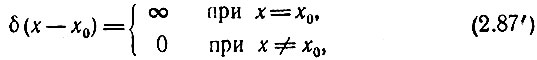
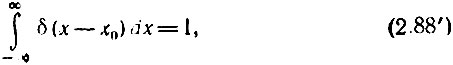
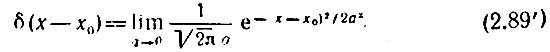
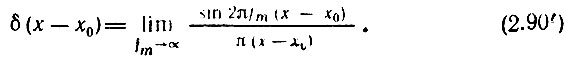
Функция δ(х) обладает важными свойствами, благодаря которым она получила широкое распространение в математике, физике и технике.
Из определений (2.87'), (2.88') вытекает основное соотношение
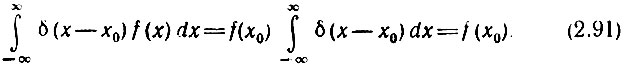
Так как по определению функция δ(х - х0) равна нулю на всей оси х, кроме точки х = х0 (где она бесконечно велика), то промежуток интегрирования можно сделать сколь угодно малым, лишь бы он включал в себя точку х0. В этом промежутке функции f(х) принимает постоянное значение f(х0), которое можно вынести за знак интеграла. Таким образом, умножение любой подынтегральной функции f(х) на δ(х - х0) позволяет приравнять интеграл произведения значению f(х) в точке х = х0.
В математике соотношение (2.91) называется фильтрующим свойством дельта-функции*.
* (На языке техники более подходящим по смыслу являлся бы термин стробирующее свойство.)
В теории сигналов приходится иметь дело с дельта-функциями от аргументов t или ω, в зависимости от того, в какой области рассматривается функция - во временной или частотной.
Рассмотрим сначала свойства функции δ(t). В этом случае основное значение имеет спектральная характеристика дельта-функции. В § 2.9 было установлено, что при сокращении длительности τи прямоугольного импульса (неизменной амплитуды) ширина основного лепестка спектральной плотности увеличивается, а величина S(0) быстро уменьшается. В данном же случае, когда сокращение длительности импульса сопровождается одновременным увеличением его амплитуды, величина спектральной плотности остается неизменной и равной величине S(0) = 1 для всех частот -∞ < ω < ω. То же самое имеет место при укорочении любого из дельтообразных импульсов.
Следовательно, спектральная плотность дельта-функции вещественна и равна единице для всех частот. Из этого также вытекает, что фазовая характеристика спектра дельта-функции δ(t) равна нулю для всех частот. Это означает, что все гармонические составляющие единичного импульса при нулевых начальных фазах, суммируясь, образуют пик бесконечно большой величины в момент времени t = 0.
Аналогично функция δ(t - t0), определяющая единичный импульс в момент t0, обладает спектральной плотностью S(ω) = е-iωt0. Модуль этой функции по-прежнему равен единице, а фазовая характеристика θ(ω) = ωt0.
Найденная ранее величина спектральной плотности дельта-функции может быть получена и формально с помощью преобразования Фурье:
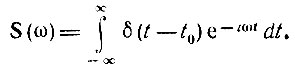
Используя свойство (2.91), находим
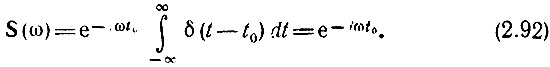
В частном случае (t0 = 0) S(ω) = 1.
Можно, очевидно, и δ(t - t0) представить в виде обратного преобразования Фурье от S(ω) = е-iωt0:
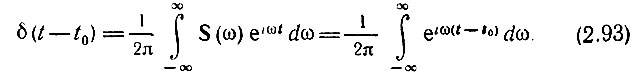
Энергия единичного импульса бесконечно велика. При спектральном рассмотрении это вытекает из равенства Парсеваля [см. (2.66)], которое при S(ω) = 1 обращается в бесконечность. При временном рассмотрении это следует из того, что энергия импульса, пропорциональная квадрату его амплитуды (т. е. величине 1/τи2) и первой степени длительности τи, с укорочением импульса растет как 1/τи. При τи → 0 энергия бесконечно велика.
Понятие единичного импульса особенно широко используется при исследовании действия коротких импульсов на линейные цепи. При этом не обязательно, чтобы амплитуда реального импульса была бесконечно велика, а длительность бесконечно мала. Достаточно, чтобы длительность импульса была мала по сравнению с постоянной времени исследуемой цепи (или по сравнению с периодом собственного колебания цепи).
Рассмотрим теперь свойства δ(ω). Все, что ранее было сказано относительно свойств δ(t), можно распространить на δ(ω) при замене t на ω и ω на t.
По аналогии с выражением (2.93) можем написать
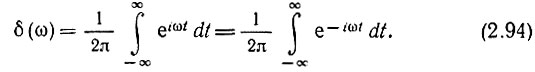
(Перемена знака в показателе степени в данном случае не влияет на величину интеграла, см. § 2.7, п. 7, а.)
Соответственно
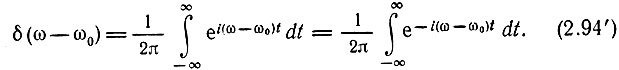

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
