2.12. Спектры некоторых неинтегрируемых функций

Одним из условий применимости преобразования Фурье к функции является ее абсолютная интегрируемость

Это условие существенно ограничивает класс функций, для которых существует спектр Фурье, выражаемый обычными функциями. Например, такие важные для теории сигналов и цепей функции, как единичный скачок (рис. 2.25, а) или включаемое в некоторый момент времени гармоническое колебание (рис. 2.25, б), не отвечают условию (2.95). Это затруднение можно преодолеть, так обобщая преобразование Фурье, чтобы при этом обеспечивалась интегрируемость некоторой вспомогательной функции.

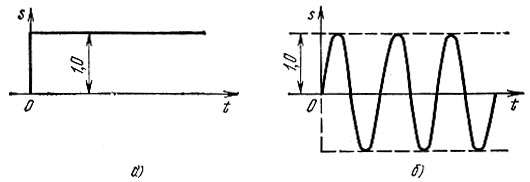
Рис. 2.25. Примеры функций, не отвечающих условию абсолютной интегрируемости

На протяжении длительного периода широко применялся способ, основанный на введении "множителя сходимости". Согласно этому способу единичный скачок сначала заменяется экспоненциальным импульсом e^-ct, с > 0, для которого условие (2.95) выполняется и спектральная плотность легко определяется

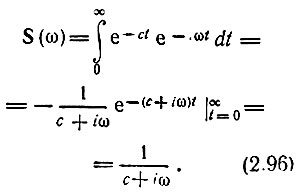
Представив S(ω) в форме (2.50), получим

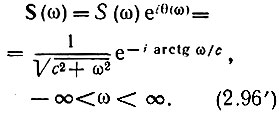
Графики Модуля 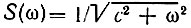(амплитудно-частотная характеристика) и аргумента θ(ω) = -arctg(ω/с) (фазочастотная характеристика) спектральной плотности экспоненциального импульса s(t) = e^-ct изображены на рис. 2.26 (штриховыми линиями).

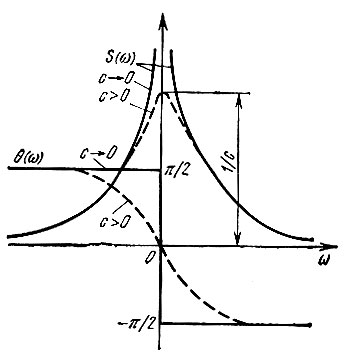
Рис. 2.26. Модуль и аргумент спектральной плотности экспоненциального импульса

Устремляя с к нулю, в пределе получаем следующие выражения для спектральной плотности единичного скачка:

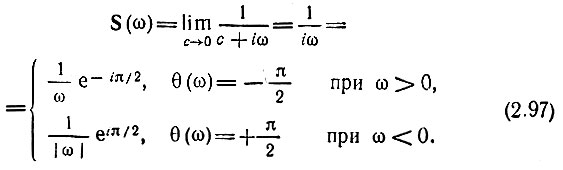
Графики S(ω) и θ(ω), вычисленные по этим формулам, изображены на рис. 2.26 сплошными линиями. Следует, однако, предупредить, что в некоторых случаях формула (2.97) может приводить к недоразумениям. При применении множителя сходимости для получения правильного результата необходимо в интеграл Фурье подставлять спектральную плотность, вычисленную при с ≠ 0, а предельный переход с → 0 совершать только в окончательном результате, после вычисления интеграла Фурье. Подобная процедура эквивалентна переходу от переменной ω к комплексной переменной р = σ + iω с соответствующим выбором пути интегрирования на плоскости р. Такой прием, приводящий к преобразованиям Лапласа, будет использован в § 2.13. В тех же случаях, когда требуется применение непосредственно фурье-спектра, введение множителя сходимости e^-ct нежелательно. Значительно эффективнее оказывается применение так называемых "обобщенных функций", к которым принадлежит и дельта-функция.

Рассмотренные в предыдущем параграфе свойства дельта-функции позволяют, в частности, распространить понятие спектральной плотности на гармоническое и вообще на любое периодическое колебание.

Рассмотрим, например, гармоническое колебание s(t) = А₀cos(ω₀t + θ₀) и, не обращая внимания на то, что такой сигнал не является абсолютно интегрируемым, выражение для спектральной плотности запишем в форме (2.48):

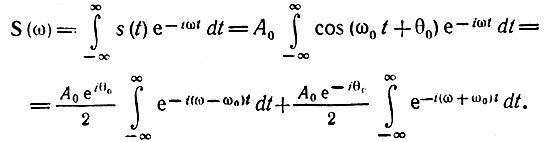
На основании формулы (2.94') получаем

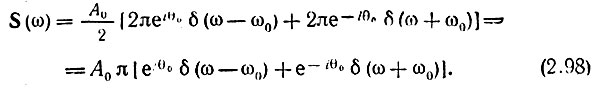
Эта функция равна нулю для всех частот, кроме ω = ω₀ и ω = -ω₀, при которых S(ω) обращается в бесконечность. Как и следовало ожидать, гармоническому колебанию с конечной амплитудой соответствует бесконечно большая спектральная плотность при дискретных частотах ω₀ и -ω₀.

В частности, приравнивая ω₀ нулю, получаем спектральную плотность сигнала в виде постоянного напряжения А₀:

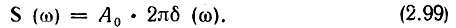
Распространив соотношение (2.98) на все гармоники любого периодического сигнала

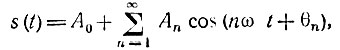
мы можем ввести понятие спектральной плотности периодического сигнала в виде суммы дельта-функций:

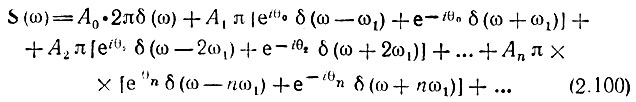
Такой подход оказывается полезным при рассмотрении смеси импульсного сигнала и монохроматических колебаний.

Пусть, например, отыскивается спектр суммы двух сигналов: импульсного s₁(t) и монохроматического s₂(t) = A₀cosω₀t (рис. 2.27, а). Применяя выражение (2.48) к s₁(t), находим обычную спектральную плотность S₁(ω), определяющую сплошной спектр (на рис. 2.27, б заштриховано). Применение же (2.48) к s₂(t) дает спектр, определяемый выражением (2.98). На рис. 2.27, б этот спектр изображается двумя спектральными линиями, уходящими в бесконечность.

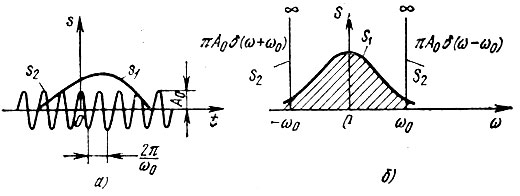
Рис. 2.27. Импульсный и монохроматический сигналы (а) и их спектральные плотности (б)

Отыщем теперь спектр единичного скачка. Для этого представим эту функцию в виде прямоугольного импульса, фронт которого расположен в точке t = 0, а срез - в точке T, стремящейся к бесконечности (рис. 2.28, а). В соответствии с таким представлением спектральную плотность единичного скачка можно определить выражением

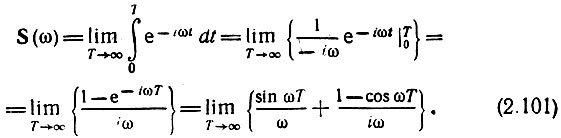
Но в соответствии с формулой (2.90)

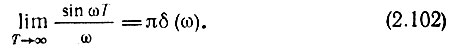
Следовательно, спектр единичного скачка

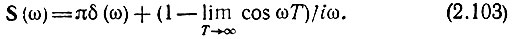
Первое слагаемое в правой части этого выражения определяет спектр постоянного напряжения А₀ = ¹/₂ [см. (2.99)], показанного на рис. 2.28, б, а второе слагаемое - спектр функции, показанной на рис. 2.28, в. Сумма этих двух функций образует единичный скачок в момент времени t = 0 (рис. 2.28, а).

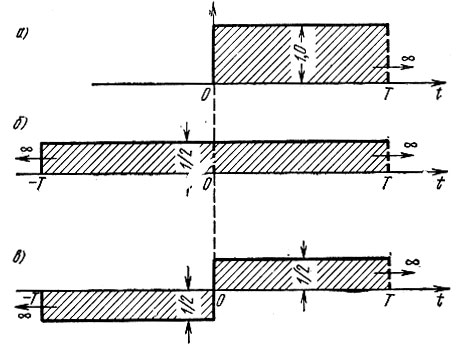
Рис. 2.28. К определению спектра единичного скачка

Рассмотрим свойства функции

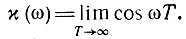
При любых значениях со, отличных от нуля, эта функция неопределенна и может принимать любые значения в пределах (-1, +1). В точке же ω = 0 указанная функция имеет определенное значение, которое легко найти. Так как мы приняли, что операция предельного перехода совершается в последнюю очередь, получаем, что при ω = 0 χ(0) = 1 независимо от величины Т.

Другое очевидное свойство χ(ω) заключается в том, что интеграл от χ(ω), взятый по любому конечному промежутку (а, b), равен нулю:

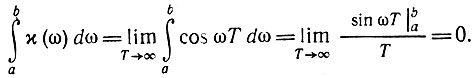
Более того, в силу леммы Римана, упомянутой в § 2.10, для любой функции g(ω), абсолютно интегрируемой в конечном промежутке (а, b), справедливы тождества

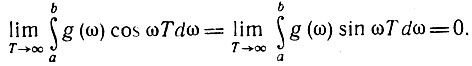
Аналогично тому, как это принято в теории обобщенных функций, можно положить, что быстро осциллирующая функция χ(ω) равна нулю для всех ω ≠ 0.

Таким образом можно ввести следующее определение:

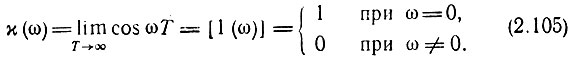
Определенную таким образом функцию χ(ω) = [1 (ω)] можно назвать игольчатой функцией (рис. 2.29).

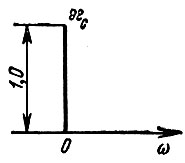
Рис. 2.29. Игольчатая функция

Применив указанные выше обозначения, за пишем формулу (2.103) в виде

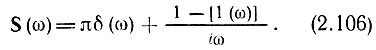
Из этого выражения видно, что при ω = 0 второе слагаемое равно нулю (так как при ω = 0 [1 (ω)] = 1) и весь вклад в спектр дает слагаемое πδ(ω), соответствующее постоянной составляющей ¹/₂. При частотах же ω, отличных от нуля, первое слагаемое равно нулю, а второе слагаемое 1/iω (так как при ω ≠ 0 [1 (ω)] = 0) [9].

Отсюда следует, что при рассмотрении воздействия единичного скачка на цепи, передаточная функция которых при ω = 0 равна нулю (т. е. на цепи, не пропускающие постоянный ток), спектральную плотность единичного скачка можно представлять в форме (2.97).