2.13. Представление сигналов на плоскости комплексной переменной

Анализ прохождения сигналов через линейные цепи, описываемые комплексной передаточной функцией, значительно облегчается при использовании методов контурного интегрирования на плоскости комплексной частоты р = σ + iω. Переход от действительной переменной ω к р = σ + iω позволяет также полностью устранить ограничения, вытекающие из требования абсолютной интегрируемости функции s(t).

Представим функцию s(t), в общем случае существующую при -∞ < t < ∞, в виде суммы двух функций

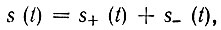
из которых s₊(t) задана при 0 < t < ∞, a s_{_}(t) при -∞ t < 0.

Обращаясь к паре преобразований Фурье (2.48), (2.49), совершим переход от ω к р сначала для функции s₊(t). Для этого домножим s₊(t) на e^-σ₁t, где σ₁ > 0 выберем таким образом, чтобы обеспечивалась абсолютная интегрируемость функции e^-σ₁ts₊(t) в пределах 0 < t < ∞. Тогда после подстановки р = σ₁ + iω выражение (2.49) можно привести к виду

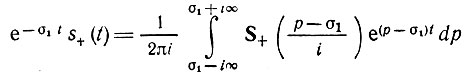
или

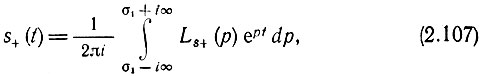
где

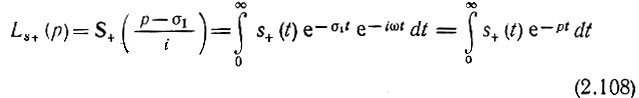
называется преобразованием Лапласа функции s₊(t).

Соотношение (2.107) по аналогии с выражением (2.49) часто называют обратным преобразованием Лапласа.

Из сравнения выражений (2.107) и (2.49) видно, что переход от ω к р означает изменение пути интегрирования. В выражении (2.49) интегрирование ведется по действительной оси ω, а в выражении (2.107) - по прямой, проходящей параллельно мнимой оси iω на расстоянии σ₁ вправо от этой оси (рис. 2.30, а). Величина постоянной σ₁ определяется характером подынтегральной функции в (2.107): путь интегрирования должен проходить правее полюсов этой функции.

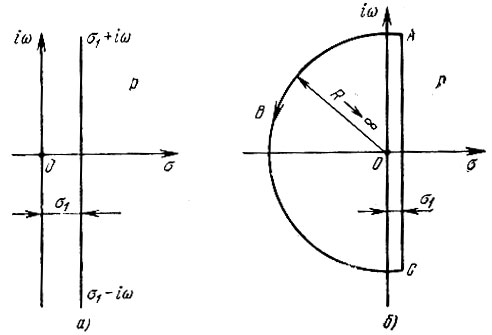
Рис. 2.30. Путь интегрирования по прямой σ₁ - i∞, σ₁ + i∞ на p-плоскости (а); образование замкнутого контура добавлением дуги ABC при R→∞ (б)

Добавлением к прямой σ₁ - i∞, σ₁ + i∞ дуги бесконечно большого радиуса можно образовать замкнутый контур интегрирования (рис. 2.30, б). Для того чтобы добавление этой дуги не изменяло величины интеграла, нужно руководствоваться следующим правилом: при положительных значениях t контур должен быть расположен в левой полуплоскости переменного р, а при отрицательных t - в правой.

Тогда в первом случае при t > 0 [при проведении дуги в левой полуплоскости (рис. 2.31, а)] контур интегрирования охватывает все полюса подынтегральной функции (лежащие левее прямой σ₁ - i∞, σ₁ + i∞) и в соответствии с теорией вычетов интеграл (2.107) определяется как

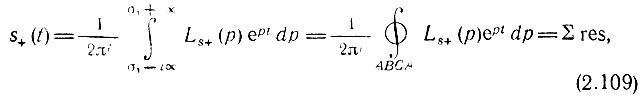
где ∑ res - сумма вычетов в полюсах подынтегральной функции.

При проведении же дуги в правой полуплоскости, т. е. при l < 0 (рис. 2.31, б), полюса функции L_s+(р)е^pt оказываются вне контура интегрирования, и в соответствии с теоремой Коши интеграл по замкнутому контуру равен нулю.

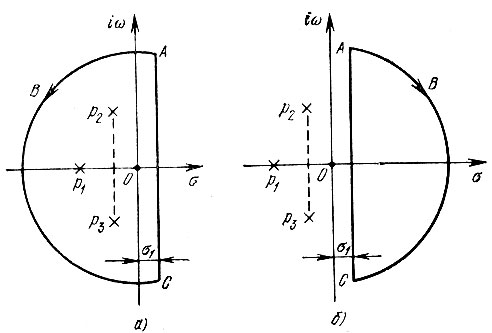
Рис. 2.31. Замыкание контура интегрирования для представления функции s₊(t): а - при t > 0; б - при t < 0

Таким образом, в зависимости от способа замыкания контура интегрирования получим

при t > 0 (контур по рис. 2.31, а)

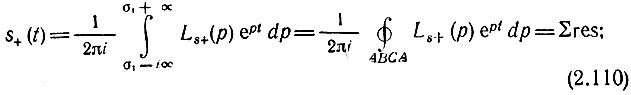
при t < 0 (контур по рис. 2.31, б)

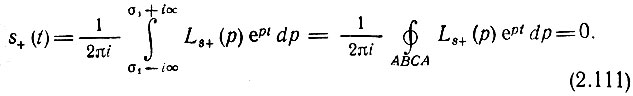
Напомним важное свойство контурных интегралов: величина интеграла не зависит от формы замкнутого контура, по которому производится интегрирование, если только полюса подынтегральной функции остаются внутри контура. На основании этого свойства контур, образованный добавлением дуги АВС бесконечно большого радиуса (рис. 2.31, а) к прямой σ₁ - i∞, σ₁ + i∞, можно произвольно деформировать при соблюдении условия, что все полюса, расположенные левее прямой σ₁ - i∞, σ₁ + i∞, остаются внутри контура.

Итак, вычисление интеграла (2.109) сводится к определению вычетов в полюсах подынтегральной функции.

Рассуждения, аналогичные предыдущим, можно провести для функции s_{_}(t), заданной при -∞ < t < 0. Домножив s_-(t) на е^-σ₂t, при σ₂ < 0, выбранной таким образом, чтобы обеспечивалась абсолютная интегрируемость функции e^-σ₂ts_-(t) в пределах -∞ < t < 0, можем написать

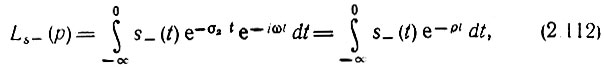
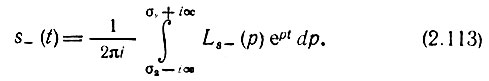
Контур интегрирования для данного случая показан на рис. 2.32. Интеграл равен сумме вычетов в полюсах функции L_s-(р)e^pt, расположенных в правой полуплоскости р. Эту сумму следует взять со знаком минус, поскольку при t < 0 контур обходится по часовой стрелке.

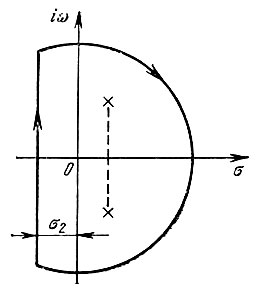
Рис. 2.32. Замыкание контура интегрирования для представления функции s_(f) при t < 0

Выражения (2.108), (2.112) и (2.107), (2.113) можно объединить следующим образом:

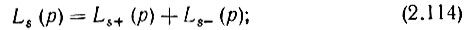
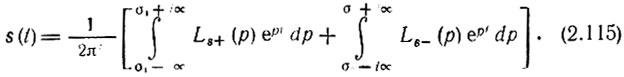
Соотношение (2.114) называется двусторонним преобразованием Лапласа.

Области сходимости функций L_s+(р) и L_{s_}(р) на плоскости р показаны на рис, 2.33. Для L_s+(р) эта область расположена справа от прямой σ = -σ₁, на которой расположены полюса (комплексно-сопряженные), а для L_{s_}(р) - слева от прямой σ = |σ₂|. Область сходимости для L_{s_}(р) имеет вид полосы шириной σ₁ + |σ₂| (рис. 2.33).

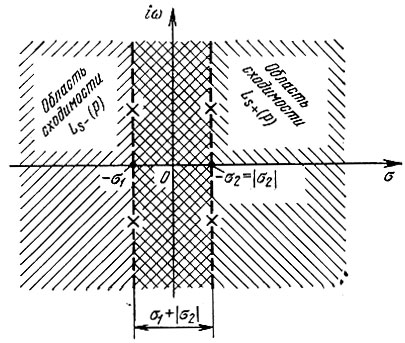
Рис. 2.33. Области сходимости при двустороннем преобразовании Лапласа

Путь интегрирования должен проходить по прямой, расположенной внутри этой полосы и параллельной оси iω, а также по замыкающей дуге, расположенной в левой полуплоскости для t > 0 и соответственно в правой полуплоскости для t < 0.

Одностороннее пребразование Лапласа получило особенно широкое распространение при анализе переходных процессов, связанных с действием на цепь внешней силы, когда начале отсчета времени совмещают с началом воздействия. Двустороннее преобразование Лапласа находит все большее распространение при анализе процессов и функций времени, двусторонних по самой своей сути (например, корреляционные функции, рассматриваемые в 2.16)).

При рассмотрении четных функций s(t) = s(-t), когда можно считать s₊(t) = s_-(-t), имеет место следующее соотношение:

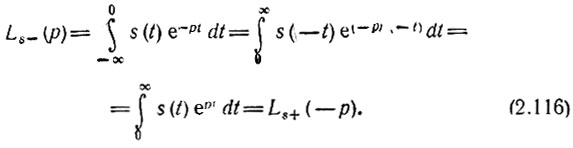
Поясним применение выражений (2.114)-(2.116) на примере функции времени (рис. 2.34) при α₁ > 0 и α₂ < 0:

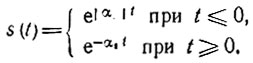
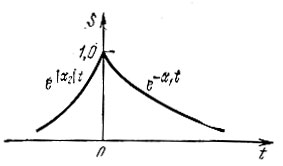
Рис. 2.34. Пример функции времени требующей применения двустороннего преобразования Лапласа

По формулам (2.112) и (2.108) находим

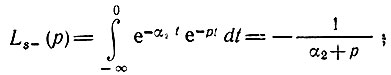
полюс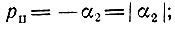

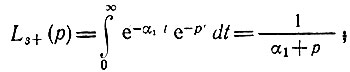
полюс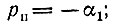

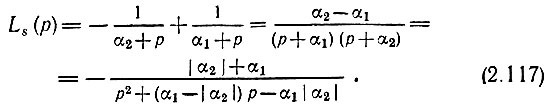
В частном случае 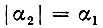получаем

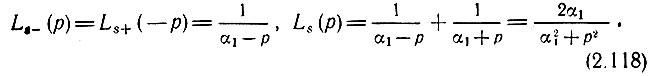
Отметим, что для перехода от изображения Лапласа к фурье-спектру S(ω) достаточно в выражении вида (2.118) заменить р на iω.

Таким образом, в рассматриваемом примере

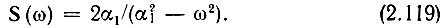
Изображение по Лапласу и соответствующие им фурье-спектры некоторых распространенных в теории сигналов функций приведены в табл. 2.1.

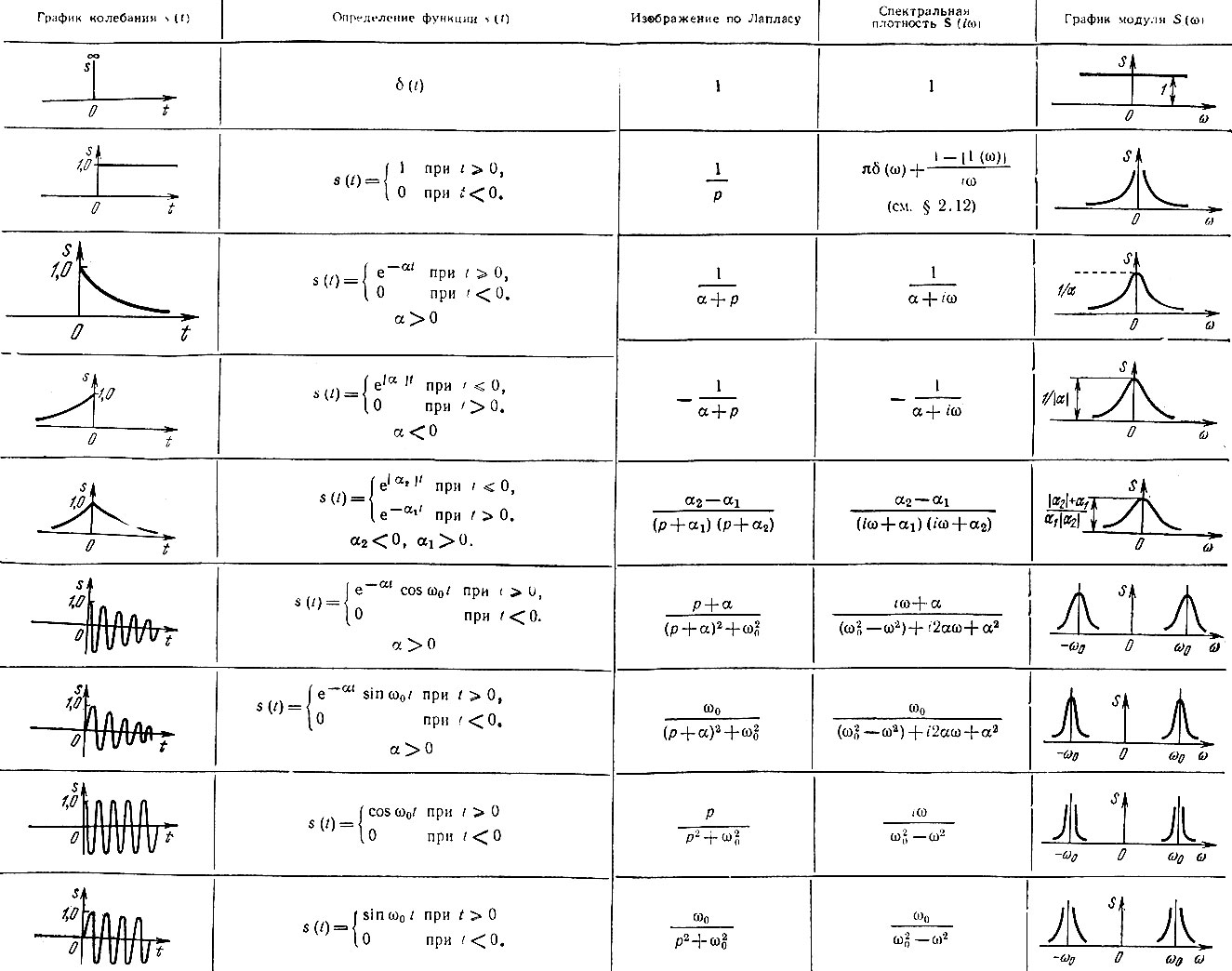
Таблица 2.1