2.15. Теорема отсчетов в частотной области

Иногда сигнал необходимо представить с помощью частотных выборок спектральной функции S(ω), а не временных выборок функции s(t). Для функции S(ω) можно составить ряд, аналогичный выражению (2.120). Это нетрудно сделать на основании взаимной заменяемости переменных t и ω в преобразованиях Фурье. Применительно к выражению (2.120) это означает, что t следует поменять на ω, 2ω_m на Т_c, 2f_m на Т_с/2π и Δt = 1/2f_m на Δω = 2ππ/Т_с.

Таким образом, получаем

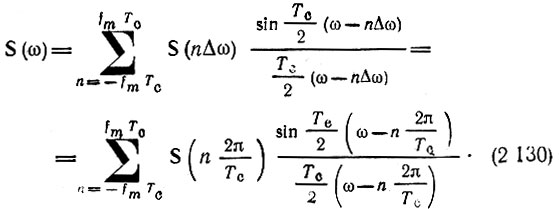
Расстановка частотных выборок иллюстрируется рис. 2.37, Если ранее временной интервал между двумя соседними выборками не должен был превышать 2π/2ω_m, то теперь частотный интервал не должен превышать 2π/Т_c. При ширине спектра 2ω_m, охватывающей область частот -ω_m < ω < ω_m, число выборок равно 2ω_m/Δω = 2f_mT_с, как и при представлении сигнала рядом (2.127).

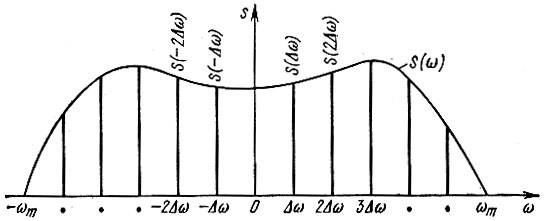
Рис. 2.37. Дискретизация спектра сигнала по Котельникову

В общем случае выборки S(n2π/Т_с) являются комплексными числами и в каждой отсчетной точке на оси частот должны быть заданы два параметра - действительная и мнимая части S(n2π/Т_с) (или модуль и аргумент). Таким образом, общее число параметров получается вдвое большим, чем при временном представлении сигнала, когда выборки s(n/2f_m) - действительные числа. Избыточность представления сигнала в частотной области легко устраняется, если учесть, что S(n2π/Т_с) и S(-π/Т_с) являются комплексно-сопряженными функциями, так что задание одной из них однозначно определяет другую, Таким образом, спектр сигнала полностью характеризуется совокупностью комплексных выборок, взятых только в области положительных частот, и число независимых параметров или степеней свободы сигнала равно 2f_mT_c, как и при представлении сигнала во временной области.