2.16. Корреляционный анализ детерминированных сигналов

Наряду со спектральным подходом к описанию сигналов часто на практике оказывается необходимой характеристика, которая давала бы представление о некоторых свойствах сигнала, в частности о скорости изменения во времени, а также о длительности сигнала без разложения его на гармонические составляющие.

В качестве такой временной характеристики широко используется корреляционная функция сигнала.

Для детерминированного сигнала s(t) конечной длительности корреляционная функция определяется следующим выражением:

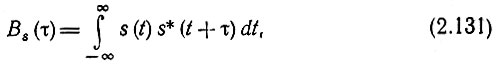
где τ - величина временного сдвига сигнала.

В данной главе рассматриваются сигналы, являющиеся вещественной функцией времени, и обозначение комплексного сопряжения можно опустить:

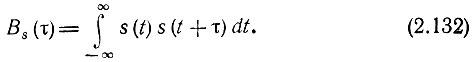
Из выражения (2.132) видно, что В_s(τ) характеризует степень связи (корреляции) сигнала s(t) со своей копией, сдвинутой на величину τ по оси времени. Ясно, что функция В_s(τ) достигает максимума при τ = 0, так как любой сигнал полностью коррелирован с самим собой. При этом

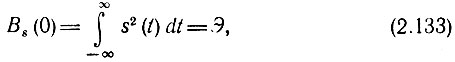
т. е. максимальное значение корреляционной функции равно энергии сигнала.

С увеличением τ функция В_s(τ) убывает (не обязательно монотонно) и при относительном сдвиге сигналов s(t) и s(t + τ) на величину, превышающую длительность сигнала, обращается в нуль.

На рис. 2.38 показано построение корреляционной функции для простейшего сигнала в виде прямоугольного импульса (рис. 2.38, а). Сдвинутый на τ (в сторону опережения) сигнал s(t + τ) показан на рис. 2.38, б, а произведение s(t) s(t + τ) - на рис. 2.38, в. График функции В_s(τ) изображен на рис. 2.38, г. Каждому значению τ соответствует свое произведение s(t) s(t + τ) и площадь под графиком функции s(t) s(t + τ). Численные значения таких площадей для соответствующих τ и дают ординаты функции B_s(τ).

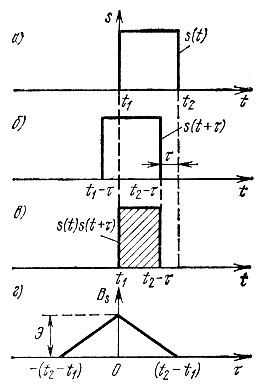
Рис. 2.38. Построение корреляционной функции для прямоугольного импульса

Аналогичное построение для треугольного импульса изображено на рис. 2.39. Из общего определения корреляционной функции, а также из приведенных примеров видно, что безразлично, вправо или влево относительно своей копии сдвигать сигнал на величину τ. Поэтому выражение (2.132) можно обобщить следующим образом:

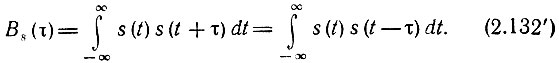
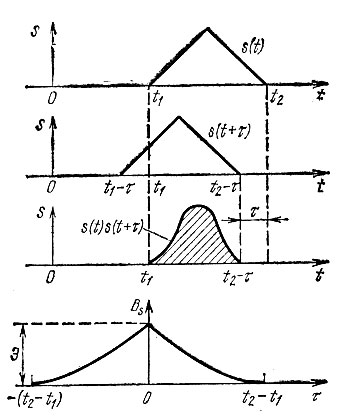
Рис. 2.39. Построение корреляционной функции для треугольного импульса

Это равносильно утверждению, что В_s(τ) является четной функцией τ.

На рис. 2.40, а показан сигнал в виде пачки из четырех одинаковых импульсов, сдвинутых один относительно другого на время Т₁, а на рис. 2.40, б - соответствующая этому сигналу корреляционная функция. Вблизи значений τ, равных 0, ±T₁, ±2T₁ и ±3T₁, эта функция имеет такой же вид, как и для одиночного импульса (см. рис. 2.38, г). Максимальное значение корреляционной функции (при τ = 0) равно учетверенной энергии одного импульса.

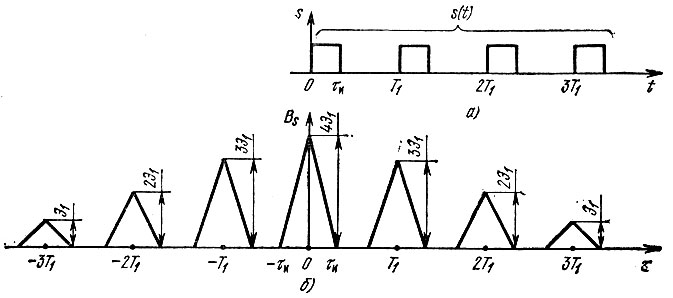
Рис. 2.40. Пачка из четырех прямоугольных импульсов (а) и корреляционная функция (б)

Для периодического сигнала, энергия которого бесконечно велика, определение корреляционной функции с помощью выражений (2.132) или (2.132') неприемлемо. В этом случае исходят из следующего определения:

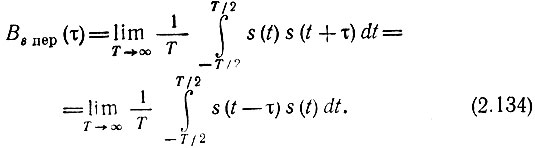
При таком определении корреляционная функция приобретает размерность мощности, причем B_{s пер}(0) равна средней мощности периодического сигнала. Ввиду периодичности сигнала s(t) усреднение произведения s(t) s(t + τ) или s(t - τ) s(t) по бесконечно большому отрезку T должно совпадать с усреднением по периоду Т₁. Поэтому выражение (2.134) можно заменить выражением

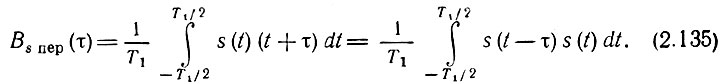
Входящие в это выражение интегралы суть не что иное, как корреляционная функция сигнала на интервале Т₁. Обозначая ее через B_sT1(τ), приходим к соотношению

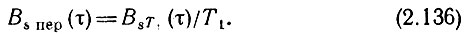
Из (2.135) вытекает также очевидное утверждение: периодическому сигналу s(t) соответствует и периодическая корреляционная функция B_{s пep}(τ). Период функции B_{s пep}(τ) совпадает с периодом Т₁ исходного сигнала s(t). Так, например, для простейшего (гармонического) сигнала s(t) = А₀ cos(ω₀t + θ₀) корреляционная функция

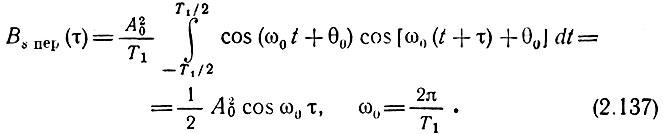
При τ = 0 B_{s пep}(0) = ¹/₂ А₀² есть средняя мощность гармонического колебания с амплитудой А₀. Важно отметить, что корреляционная функция B_{s пер}(τ) не зависит от начальной фазы колебания θ₀.

На рис. 2.41, б изображена корреляционная функция сигнала, представляющего собой периодическую последовательность прямоугольных импульсов (рис. 2.41, а). Каждый из импульсов функции В_{s пер}(τ) совпадает по форме с корреляционной функцией одиночного импульса из периодической последовательности s(t). Однако в данном случае максимальные ординаты B_{s пер}(τ) равны не энергии (как на рис. 2.40), а средней мощности сигнала s(t), т. е. величине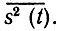

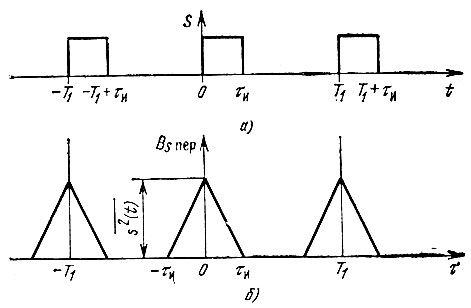
Рис. 2.41. Периодическая последовательность импульсов (а) и ее корреляционная функция (б)

Для оценки степени связи между двумя различными сигналами s₁(t) и s₂(t) используется взаимно-корреляционная функция, определяемая общим, выражением

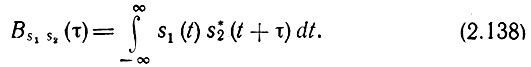
Для вещественных функций s₁(t) и s₂(t)

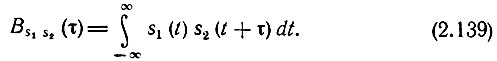
Рассмотренная выше корреляционная функция B_s(τ) является частным случаем функции В_s1s2(τ), когда s₁(t) = s₂(t).

Построение взаимно-корреляционной функции для двух сигналов s₁(t) и s₂(t) приведено на рис. 2.42. Исходное положение сигналов (τ = 0) показано на рис. 2.42, а. При сдвиге сигнала s₂(t) влево (τ > 0, рис. 2.42, б) корреляционная функция сначала возрастает, затем убывает до нуля при τ = Т. При сдвиге вправо (τ < 0) корреляционная функция сразу убывает. В результате получается асимметричная относительно оси ординат функция B_S1S2 (рис. 2.42, в).

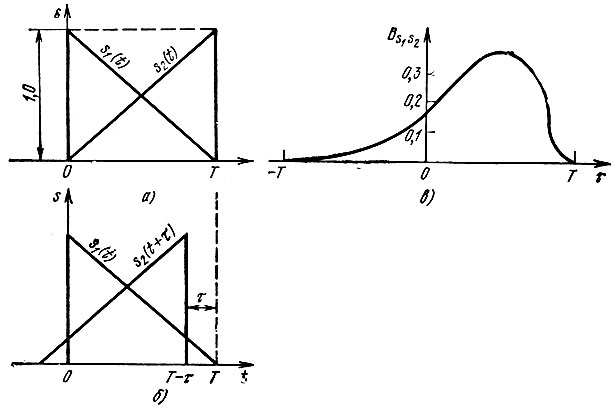
Рис 2.42. Построение взаимно-корреляционной функции: а - исходное положение сигналов; б - сдвиг сигнала s₂(t) на τ; в - взаимно-корреляционная функция

Очевидно, что значение B_S1S2 не изменится, если вместо упреждения сигнала s₂(t) дать задержку сигналу s₁(t). Поэтому выражение (2.139) можно обобщить следующим образом:

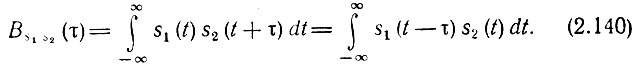
Следует, однако, различать выражения (2.132') и (2.140). В отличие от В_s(τ) взаимно-корреляционная функция не обязательно является четной относительно τ. Кроме того, взаимно-корреляционная функция не обязательно достигает максимума при τ = 0. Оба эти свойства функции B_S1S2(τ) иллюстрируются рис. 2.42.