2.17. Соотношение между корреляционной функцией и спектральной характеристикой сигнала

Воспользуемся выражением (2.63), в котором положим f(t) = s(t), g(t) = s(t + τ) и соответственно F(ω) = S(ω); G(ω) = S(ω) е^iωτ. Тогда получим

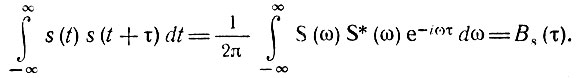
Учитывая, что 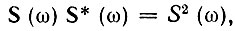приходим к искомому соотношению

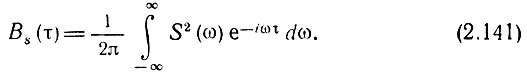
На основании известных свойств преобразований Фурье можно также написать^*

^* (Ввиду четности функции В_s(τ) знак перед ωτ в показателе степени может быть произвольным. То же относится к (2.141).)

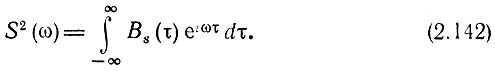
Итак, прямое преобразование Фурье (2.142) корреляционной функции B_s(τ) дает спектральную плотность энергии (см. замечание в конце § 2.8), а преобразование (2.141) дает корреляционную функцию В_s(τ).

Из выражений (2.141) и (2.142) вытекают свойства, аналогичные отмеченным в § 2.10: чем шире спектр S(ω) сигнала, тем меньше интервал корреляции, т. е. величина сдвига τ, в пределах которого корреляционная функция отлична от нуля. Соответственно чем больше интервал корреляции заданного сигнала, тем уже его спектр.

Из выражений (2.141) и (2.142) также видно, что корреляционная функция В_s(τ) не зависит от фазовой характеристики спектра сигнала. Так как при, заданном амплитудном спектре S(ω) форма функции s(t) существенно зависит от фазового спектра, то можно сделать следующее заключение: различным по форме сигналам s(t), обладающим одинаковыми амплитудными спектрами, соответствуют одинаковые корреляционные функции В_s(τ).