2.18. Когерентность

В физике, где впервые был применен термин "когерентные колебания", под когерентностью подразумевалось совпадение фаз суммируемых гармонических колебаний. В настоящее время в радиотехнике и теории информации когерентность трактуется более широко: под когерентностью обычно подразумевается связь между фазами сигналов.

Степень когерентности сигналов можно оценивать с помощью сопоставления энергии суммы сигналов с суммой энергий отдельных слагаемых сигналов.

Пусть, например, рассматриваются два сигнала s₁(t) и s₂(t). Энергия их суммы в общем случае

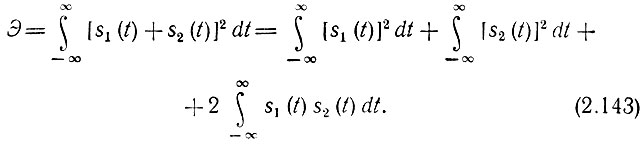
Первые два интеграла в правой части этого выражения определяют энергии Э₁ и Э₂ сигналов s₁(t) и s₂(t), взятых отдельно, а последний определяет "энергию взаимодействия" Э₁₂ между рассматриваемыми сигналами.

В обозначениях, используемых при корреляционном анализе сигналов (см. § 2.16 и 2.17), выражение (2.143) принимает вид

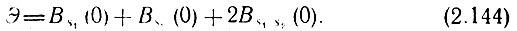
Таким образом, введенная в § 2.16 взаимно-корреляционная функция [см. (2.139)] B_s1s2(τ) при τ = 0 может служить мерой энергии взаимодействия Э₁₂.

Чем большую долю от суммы Э₁ + Э₂ составляет энергия взаимодействия Э₁₂, тем выше когерентность сигналов s₁(t) и s₂(t).

В качестве меры когерентности иногда принимают иной критерий, а именно отношение

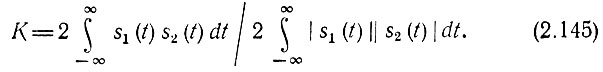
Числитель этого отношения представляет собой энергию взаимодействия Э₁₂, а величина отношения может принимать любые значения, заключенные между -1 и +1.

Рассмотрим в качестве примера два одинаковых сигнала с равными энергиями Э₁ = Э₂. При сложении этих сигналов "в фазе" суммарная энергия Э = 4Э₁ = 4Э₂, а Э₁₂ = 2Э₁ = 2Э₂. Знаменатель дроби в правой части (2.145) при этом равен Э₁ + Э₂ (так же, как и числитель) и К = +1.

При сложении в противофазе (т. е. при вычитании) Э = 0, а К = -1. В обоих случаях сигналы полностью когерентны.

Для того чтобы сигналы были некогерентны (т. е. чтобы К = 0), должно выполняться условие

Но это условие есть не что иное, как условие ортогональности рассматриваемых сигналов.

Таким образом, приходим к выводу, что некогерентные сигналы обязательно являются ортогональными. Из ортогональности некогерентных сигналов следует, что при линейном их сложении энергия суммы сигналов равна сумме энергий отдельных слагаемых.