3.4. Угловая модуляция. Фаза и мгновенная частота колебания

В случае простого гармонического колебания

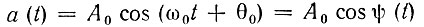
набег фазы за какой-либо конечный промежуток времени от t = t₁ до t = t₂ будет равен

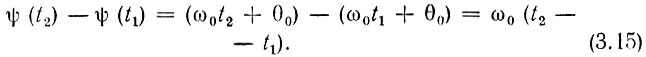
Отсюда видно, что при постоянной угловой частоте набег фазы за какой-либо промежуток времени пропорционален длительности этого промежутка.

С другой стороны, если известно, что набег фазы за время t₂ - t₁ равен ψ(t₂) - ψ(t₁), то угловую частоту можно определить как отношение

если, конечно, имеется уверенность, что в течение рассматриваемого промежутка времени частота сохраняла постоянное значение.

Из (3.16) видно, что угловая частота есть не что иное, как скорость изменения фазы колебания.

Переходя к сложному колебанию, у которого частота может изменяться во времени, необходимо равенства (3.15), (3.16) заменить интегральным и дифференциальным соотношениями

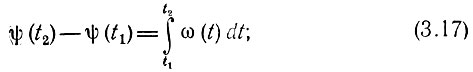
В этих выражениях ω(t) = 2πf(t) - мгновенная угловая частота колебания; f(t) - мгновенная частота, Гц.

Согласно выражениям (3.17), (3.18) полную фазу высокочастотного колебания в момент t можно определить как

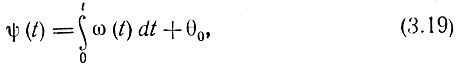
где первое слагаемое в правой части определяет набег фазы за время от начала отсчета до рассматриваемого момента t, а θ₀ - начальная фаза колебания (в момент t = 0).

При таком подходе фазу ψ(t) = ω₀t + θ(t), фигурирующую в выражении (3.1), следует заменить на

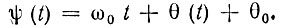
Итак, общее выражение для высокочастотного колебания, амплитуда которого постоянна, т. е. А(t) = А₀, а аргумент ψ(t) модулирован, можно представить в форме

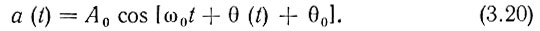
Соотношения (3.18), (3.19), устанавливающие связь между изменениями частоты и фазы, указывают на общность двух разновидностей угловой модуляции - частотной и фазовой.

Поясним соотношения (3.18)-(3.20) на примере простейшей гармонической частотной модуляции, когда мгновенная частота колебания определяется выражением

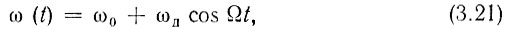
где ω_д = 2πf_д представляет собой амплитуду частотного отклонения. Для краткости ω_д в дальнейшем будем называть девиацией частоты или просто девиацией. Через ω₀ и Ω, как и при амплитудной модуляции, обозначены несущая частота и модулирующая частота.

Составим выражение для мгновенного значения колебания (тока или напряжения), частота которого изменяется по закону (3.21), а амплитуда постоянна.

Подставляя в (3.19) ω(t) из уравнения (3.21), получаем

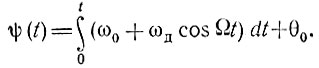
Выполнив интегрирование, найдем

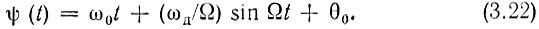
Таким образом,

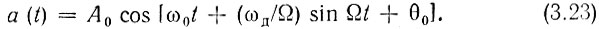
Фаза колебания а(t) наряду с линейно возрастающим слагаемым ω₀t содержит еще периодическое слагаемое (ω_д/Ω) sin Ωt. Это позволяет рассматривать а(t) как колебание, модулированное по фазе. Закон этой модуляции является интегральным по отношению к исходной частотной модуляции. Именно модуляция частоты по закону ω_д cos Ωt приводит к модуляции фазы по закону (ω_д/Ω) sin Ωt. Амплитуду изменения фазы

часто называют индексом угловой модуляции.

Заметим, что индекс модуляции совершенно не зависит от средней (немодулированной) частоты ω₀, а определяется исключительно величиной девиации ω_д и модулирующей частотой Ω.

Рассмотрим теперь противоположный случай, когда стабильное по частоте и фазе колебание пропускается через устройство, осуществляющее периодическую модуляцию фазы по закону 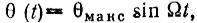так что колебание на выходе устройства имеет вид

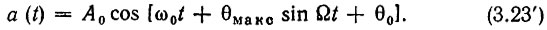
Какова частота этого колебания? Используя выражение (3.18), находим

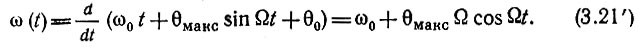
Учитывая соотношение (3.24), приходим к выводу, что θ_максΩ = ω_д. Таким образом, гармоническая модуляция фазы с индексом θ_макс эквивалентна частотной модуляции с девиацией ω_д = θ_максΩ.

Из приведенного примера видно, что при гармонической угловой модуляции по характеру колебания нельзя заключить, с какой модуляцией мы имеем дело - с частотной или фазовой. В обоих случаях вектор ОА, изображающий на векторной диаграмме модулированное колебание, качается относительно своего исходного положения таким образом, что угол θ (рис. 3.12) изменяется во времени по закону θ = θ_макс sin Ωt при фазовой модуляции, θ = (ω_д/Ω) sin Ωt = θ_макс sin Ωt при частотной модуляции (когда Δ = ω_д cos Ωt). Цифрами I, II, III и IV отмечено положение вектора ОА при Ωt = 0, π/2, π и 3π/2.

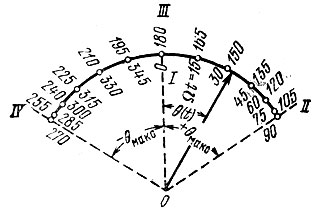
Рис. 3.12. Представление высокочастотного колебания при угловой модуляции в виде качающего вектора

Различие между частотной и фазовой модуляцией проявляется при изменении частоты модуляции.

При частотной модуляции величина девиации ω_д пропорциональна амплитуде модулирующего напряжения и не зависит от частоты модуляции Ω.

При фазовой модуляции величина θ_макс пропорциональна амплитуде модулирующего напряжения и не зависит от частоты модуляции Ω.

Эти положения поясняются рис. 3.13 и 3.14, на которых показаны частотные характеристики величин 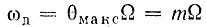при частотной и фазовой модуляции. В обоих случаях предполагается, что на вход модулятора подается модулирующее напряжение с неизменной амплитудой U, а частота Ω изменяется от Ω_мин до Ω_макс.

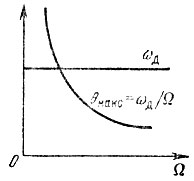
Рис. 3.13. Зависимость девиации ω_д и индекса m от модулирующей частоты ЧМ

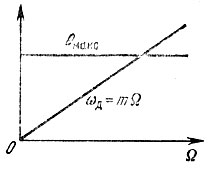
Рис. 3.14. Зависимость m и девиации ω_д от модулирующей частоты при ФМ

В первом случае, т. е. при частотной модуляции, величина ω_д, зависящая, как указывалось выше, только от амплитуды U, будет постоянной величиной. Величина же индекса модуляции m = ω_д/Ω = θ_макс с увеличением частоты будет убывать (рис. 3.13). Во втором случае, т. е. при фазовой модуляции, θ_макс не зависит от Ω, а ω_д = θ_максΩ = mΩ изменяется пропорционально частоте модуляции (рис. 3.14).

Если на вход модулятора подается не гармоническое, а сложное напряжение, то структура модулированного колебания различна при ЧМ и ФМ. В первом случае медленным изменениям сигнала, т. е. низким частотам, соответствуют очень большие значения θ_макс (рис. 3.13), а во втором - очень малые значения ω_д (рис. 3.14).

Поясним это на примере. Пусть на вход частотного и фазового модуляторов подается одинаковое синусоидальное напряжение, частота которого изменяется от F_мин = 200 Гц до F_макс = 2000 Гц. При частотной модуляции зададим f_д = 20 кГц, а при фазовой модуляции θ_макс = 0,5 рад, причем эти величины при заданной и неизменной амплитуде U остаются неизменными в полосе от 200 до 2000 Гц. Тогда при ЧМ максимальное значение фазового отклонения при F_мин будет равно

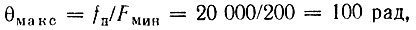
минимальное же значение фазового отклонения при F_макс составит

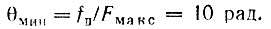
При фазовой модуляции минимальная девиация, равная f_{д мин} = θ_максF_мин = 100 Гц, будет при нижней частоте модуляции F_мин. Максимальная же девиация, равная f_{д макс} = θ_максF_макс = 1000 Гц, будет при верхней частоте модуляции.

Помимо различия в структуре колебания (при модуляции сложным сигналом), частотная и фазовая модуляции различаются по способу осуществления. В первом случае обычно применяется прямое воздействие на частоту колебаний генератора. При фазовой модуляции генератор дает стабильную частоту, а фаза колебания модулируется в одном из последующих элементов устройства.