3.5. Спектр колебания при угловой модуляции. Общие соотношения

Пусть задано колебание

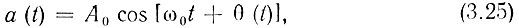
относительно которого известно, что передаваемое сообщение s(t) заложено в функцию θ(t). Если колебание a(t) получено с помощью фазовой модуляции, то θ(t) и s(t) полностью совпадают по форме и отличаются лишь постоянным коэффициентом. При этом, очевидно, с точностью до постоянного коэффициента совпадают и спектры функций θ(t) и s(t). В случае же частотной модуляции функция θ(t) является интегралом от передаваемого сообщения s(t). Это вытекает из выражений (3.19) и (3.20). Так как интегрирование является линейным преобразованием, то при частотной модуляции спектр функции θ(t) состоит из тех же компонентов, что и спектр сообщения s(t), но с измененными амплитудами и фазами.

Отвлекаясь от способа осуществления угловой модуляции - фазовой или частотной и считая известным и заданным спектр функции θ(t), найдем спектр модулированного колебания а(t). Для этого выражение (3.25) преобразуем к виду

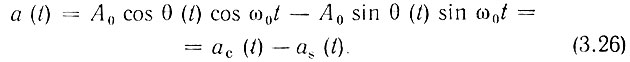
Из (3.26) следует, что модулированное по углу колебание можно рассматривать как сумму двух квадратурных колебаний; косинусного а_с(t) = A₀ cos θ(t) cos ω₀t и синусного a_s(t) = A₀ sin θ(t) × sin ω₀t, каждое из которых модулировано только по амплитуде; для косинусного колебания закон амплитудной модуляции определяется медленной функцией cos θ(t), а для синусного - функцией sin θ(t). Но в § 3.3 было установлено, что для определения спектра амплитудно-модулированного колебания достаточно сдвинуть на частоту ω₀ спектр огибающей амплитуд. Следовательно, для нахождения спектра колебания а(t), определяемого выражением (3.26), необходимо сначала найти спектры функций cos θ(t) и sin θ(t), т. е. спектры огибающих квадратурных колебаний. Перенос этих спектров на частоту ω₀ можно затем осуществить таким же образом, как и при обычной амплитудной модуляции.

Из приведенных рассуждений следует, что при одном и том же передаваемом сообщении спектр колебания, модулированного по углу, значительно сложнее, чем модулированного по амплитуде. Действительно, так как cos θ(t) и sin θ(t) являются нелинейными функциями своего аргумента θ(t), то спектры этих функций могут существенно отличаться от спектра функции θ(t): возможно возникновение кратных и комбинационных частот, как это имеет место при обычных нелинейных преобразованиях спектра.

Это обстоятельство, а также наличие двух квадратурных слагаемых показывает, что при угловой модуляции спектр модулированного колебания нельзя получить простым сдвигом спектра сообщения на величину несущей частоты ω₀, как это имеет место при амплитудной модуляции. Связь между спектрами сообщения и модулированного колебания оказывается при угловой модуляции более сложной.